【数学】2020届一轮复习北师大版合情推理课时作业

【数学】2020届一轮复习北师大版合情推理课时作业

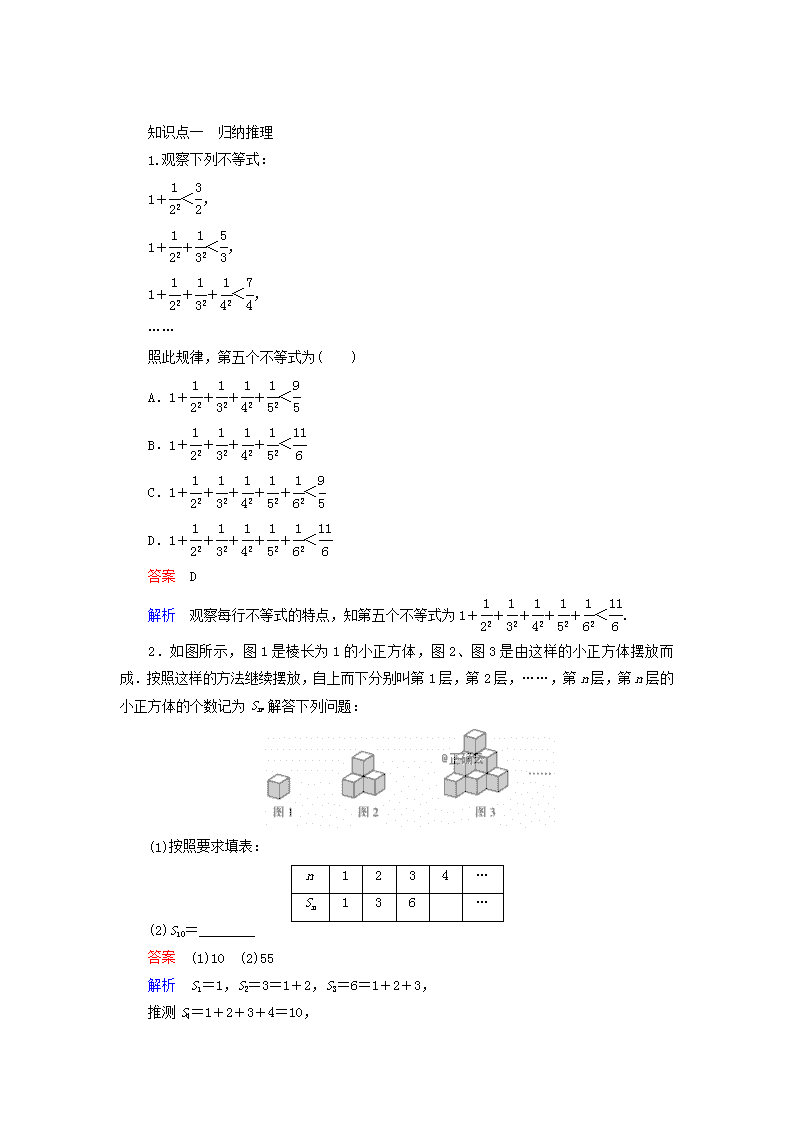
知识点一 归纳推理 ‎1.观察下列不等式：‎ ‎1＋＜，‎ ‎1＋＋＜，‎ ‎1＋＋＋＜，‎ ‎……‎ 照此规律，第五个不等式为(　　)‎ A．1＋＋＋＋＜ B．1＋＋＋＋＜ C．1＋＋＋＋＋＜ D．1＋＋＋＋＋＜ 答案　D 解析　观察每行不等式的特点，知第五个不等式为1＋＋＋＋＋＜.‎ ‎2．如图所示，图1是棱长为1的小正方体，图2、图3是由这样的小正方体摆放而成．按照这样的方法继续摆放，自上而下分别叫第1层，第2层，……，第n层，第n层的小正方体的个数记为Sn.解答下列问题：‎ ‎(1)按照要求填表：‎ n ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ Sn ‎1‎ ‎3‎ ‎6‎ ‎…‎ ‎(2)S10＝________‎ 答案　(1)10　(2)55‎ 解析　S1＝1，S2＝3＝1＋2，S3＝6＝1＋2＋3，‎ 推测S4＝1＋2＋3＋4＝10，‎ S10＝1＋2＋3＋…＋10＝55.‎ 知识点二 类比推理 ‎3.在公比为4的等比数列{bn}中，若Tn是数列{bn}的前n项积，则有，，也成等比数列，且公比为4100；类比上述结论，相应地，在公差为3的等差数列{an}中，若Sn是{an}的前n项和．可类比得到的结论是______________________．‎ 答案　数列S20－S10，S30－S20，S40－S30也是等差数列，且公差为300‎ 解析　因为等差数列{an}的公差d＝3，‎ 所以(S30－S20)－(S20－S10)‎ ‎＝(a21＋a22＋…＋a30)－(a11＋a12＋…＋a20)‎ ‎＝100d＝300，‎ 同理可得：(S40－S30)－(S30－S20)＝300，‎ 所以数列S20－S10，S30－S20，S40－S30是等差数列，且公差为300.‎ 即结论为：数列S20－S10，S30－S20，S40－S30也是等差数列，且公差为300.‎ ‎4．在Rt△ABC中，AB⊥AC，AD⊥BC于D，求证：＝＋，那么在四面体ABCD中，类比上述结论，你能得到怎样的猜想，并说明理由．‎ 解　如图①所示，由射影定理得 AD2＝BD·DC，AB2＝BD·BC，AC2＝CD·BC，‎ 所以＝ ‎＝＝.‎ 又BC2＝AB2＋AC2，‎ 所以＝＋.‎ 类比猜想：‎ 四面体ABCD中，AB，AC，AD两两垂直，AE⊥平面BCD，则＝＋＋.‎ 如图②，连接BE交CD于F，连接AF，‎ 因为AB⊥AC，AB⊥AD，AC∩AD＝A，‎ 所以AB⊥平面ACD，‎ 而AF⊂平面ACD，所以AB⊥AF，‎ 在Rt△ABF中，AE⊥BF，‎ 所以＝＋，‎ 易知在Rt△ACD中，AF⊥CD，‎ 所以＝＋，‎ 所以＝＋＋，猜想正确．‎ 知识点三 归纳和类比推理的应用 ‎5.鲁班发明锯子的思维过程为：带齿的草叶能割破行人的腿，“锯子”能“锯”开木材，它们在功能上是类似的．因此，它们在形状上也应该类似，“锯子”应该是齿形的．该过程体现了(　　)‎ A．归纳推理 B．类比推理 C．胡乱推理 D．没有推理 答案　B 解析　推理是根据一个或几个已知的判断来确定一个新的判断的思维过程，上述过程是推理，由性质类比可知是类比推理．‎ ‎6．若数列{an}(n∈N*)是等差数列，则有数列bn＝(n∈N*)也是等差数列．‎ 类比上述性质，相应地：‎ 若数列{cn}(n∈N*)是等比数列，且cn＞0，则数列dn＝________(n∈N*)也是等比数列．‎ 答案　 解析　由等差、等比数列之间运算的相似特征知，‎ ‎“和积，商开方”．‎ 容易得出dn＝也是等比数列．‎ 一、选择题 ‎1．归纳推理和类比推理的相似之处为(　　)‎ A．都是从一般到一般 B．都是从一般到特殊 C．都是从特殊到特殊 D．所得结论都不一定正确 答案　D 解析　归纳推理是由特殊到一般的推理，其结论不一定正确．类比推理是从特殊到特殊的推理，结论具有推测性，不一定可靠，故选D.‎ ‎2．下列平面图形与空间的平行六面体作为类比对象比较合适的是(　　)‎ A．三角形 B．梯形 C．平行四边形 D．矩形 答案　C 解析　由类比推理的定义和特点判断，易知选C.‎ ‎3．观察下列事实|x|＋|y|＝1的不同整数解(x，y)的个数为4，|x|＋|y|＝2的不同整数解(x，y)的个数为8，|x|＋|y|＝3的不同整数解(x，y)的个数为12，…，则|x|＋|y|＝20的不同整数解(x，y)的个数为 (　　)‎ A．76 B．80 C．86 D．92‎ 答案　B 解析　由已知条件得，|x|＋|y|＝n(n∈N*)的整数解(x，y)个数为4n，故|x|＋|y|＝20的整数解(x，y)的个数为80.‎ ‎4．如图，在所给的四个选项中，最适合填入问号处，使之呈现一定的规律性的为(　　)‎ 答案　A 解析　观察第一组中的三个图，可知每一个黑色方块都从右向左循环移动，每次移动一格，由第二组图的前两个图，可知选A.‎ ‎5．把下列在平面内成立的结论类比到空间，结论不成立的是(　　)‎ A．如果一条直线与两条平行线中的一条相交，则必与另一条相交 B．如果一条直线与两条平行线中的一条垂直，则必与另一条垂直 C．如果两条直线与第三条直线都不相交，则这两条直线不相交 D．如果两条直线同时与第三条直线垂直，则这两条直线平行 答案　D 解析　类比A的结论为：如果一个平面与两个平行平面中的一个相交，则必与另一个相交．成立．类比B的结论为：如果一个平面与两个平行平面中的一个垂直，则必与另一个垂直．成立．类比C的结论为：如果两个平面与第三个平面都不相交，则这两个平面不相交．成立．类比D的结论为：如果两个平面同时与第三个平面垂直，则这两个平面平行．不成立．‎ 二、填空题 ‎6．已知 ＝2， ＝3， ＝4，…，若 ＝6(a，b∈R)，则a＋b＝________.‎ 答案　41‎ 解析　根据题意，由于 ＝2， ＝3， ＝4，…那么可知 ＝6，a＝6，b＝6×6－1＝35，所以a＋b＝41.‎ ‎7．如图，直角坐标系中每个单元格的边长为1，由下往上的6个点1,2,3,4,5,6的横纵坐标(xi，yi)(i＝1,2,3,4,5,6)分别对应数列{an}(n∈N*)的前12项，如下表所示：‎ a1‎ a2‎ a3‎ a4‎ a5‎ a6‎ a7‎ a8‎ a9‎ a10‎ a11‎ a12‎ x1‎ y1‎ x2‎ y2‎ x3‎ y3‎ x4‎ y4‎ x5‎ y5‎ x6‎ y6‎ 按如此规律下去，则a2013＋a2014＋a2015的值为______．‎ 答案　1007‎ 解析　由题图知a1＝x1＝1，a3＝x2＝－1，a5＝x3＝2，a7＝x4＝－2，…，则a1＋a3＝a5＋a7＝…＝a2013＋a2015＝0.又a2＝y1＝1，a4＝y2＝2，a6＝y3＝3，…，则a2014＝1007，所以a2013＋a2014＋a2015＝1007.‎ 答案　＜sin 解析　运用类比推理与数形结合，可知y＝sinx(x∈(0，π))的图象是上凸的，因此线段AB的中点的纵坐标总是小于函数y＝sinx(x∈(0，π))图象上的点的纵坐标，即有＜sin成立．‎ 三、解答题 ‎9．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数．‎ ‎①sin213°＋cos217°－sin13°cos17°；‎ ‎②sin215°＋cos215°－sin15°cos15°；‎ ‎③sin218°＋cos212°－sin18°cos12°；‎ ‎④sin2(－18°)＋cos248°－sin(－18°)cos48°；‎ ‎⑤sin2(－25°)＋cos255°－sin(－25°)cos55°.‎ ‎(1)试从上述五个式子中选择一个，求出这个常数；‎ ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ 解　(1)选择②式计算如下：‎ sin215°＋cos215°－sin15°cos15°‎ ‎＝1－sin30°＝.‎ ‎(2)sin2α＋cos2(30°－α)－sinαcos(30°－α)＝.‎ 证明：sin2α＋cos2(30°－α)－sinαcos(30°－α)＝sin2α＋(cos30°cosα＋sin30°sinα)2－sinα(cos30°cosα＋sin30°·sinα)＝sin2α＋cos2α＋sinαcosα＋sin2α－sinα·cosα－sin2α＝sin2α＋cos2α＝.‎ ‎10．已知椭圆具有性质：若M，N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，kPM与kPN之积是与点P的位置无关的定值．试对双曲线－＝1写出具有类似特征的性质，并加以证明．‎ 解　类似的性质为：若M，N是双曲线－＝1上关于原点对称的两个点，点P是双曲线上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，那么kPM与kPN之积是与点P的位置无关的定值．‎ 证明：设点M，P的坐标分别为(m，n)，(x，y)，‎ 则N(－m，－n)．‎ 因为点M(m，n)在已知的双曲线上，‎ 所以n2＝m2－b2，同理，y2＝x2－b2.‎ 则kPM·kPN＝·＝＝·＝(定值)．‎