高中数学模块综合评价二达标检测含解析新人教A版必修5
模块综合评价(二)
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题中正确的是( )
A.若a,b,c是等差数列,则log2a,log2b,log2c是等比数列
B.若a,b,c是等比数列,则log2a,log2b,log2c是等差数列
C.若a,b,c是等差数列,则2a,2b,2c是等比数列
D.若a,b,c是等比数列,则2a,2b,2c是等差数列
解析:=2b-a,=2c-b,
因为a,b,c成等差数列,所以c-b=b-a,
所以2b-a=2c-b,即=.
答案:C
2.在△ABC中,A=135°,C=30°,c=20,则边a的长为( )
A.10 B.20
C.20 D.
解析:由正弦定理:=,
所以a===20.
答案:B
3.已知不等式ax2+bx+2>0的解集是(-1,2),则a+b的值为( )
A.1 B.-1
C.0 D.-2
解析:由已知得-=-1+2,=-1×2,a<0,
解得a=-1,b=1,故a+b=0.
答案:C
4.在等差数列{an}中,首项a1=0,公差d≠0,若am=a1+a2+…+a9,则m的值为( )
A.37 B.36
- 9 -
C.20 D.19
解析:由am=a1+a2+…+a9得(m-1)d=9a5=36d⇒m=37.
答案:A
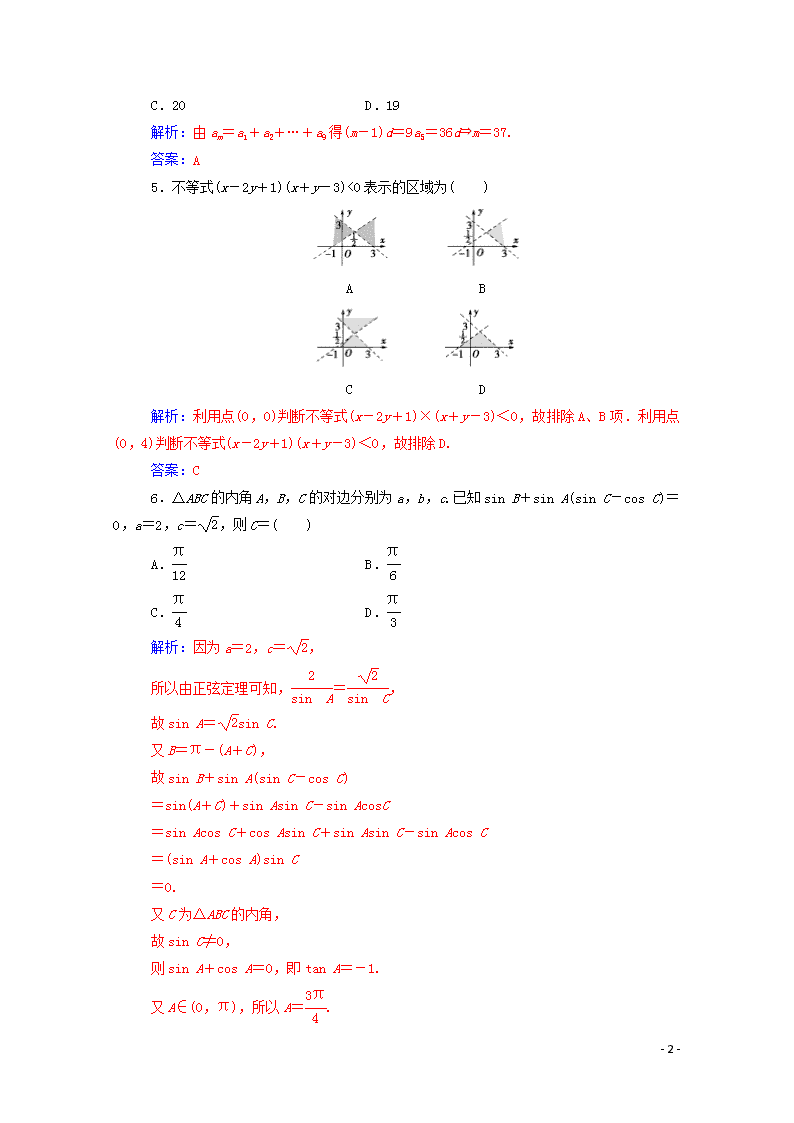
5.不等式(x-2y+1)(x+y-3)<0表示的区域为( )
A B
C D
解析:利用点(0,0)判断不等式(x-2y+1)×(x+y-3)<0,故排除A、B项.利用点(0,4)判断不等式(x-2y+1)(x+y-3)<0,故排除D.
答案:C
6.△ABC的内角A,B,C的对边分别为a,b,c.已知sin B+sin A(sin C-cos C)=0,a=2,c=,则C=( )
A. B.
C. D.
解析:因为a=2,c=,
所以由正弦定理可知,=,
故sin A=sin C.
又B=π-(A+C),
故sin B+sin A(sin C-cos C)
=sin(A+C)+sin Asin C-sin AcosC
=sin Acos C+cos Asin C+sin Asin C-sin Acos C
=(sin A+cos A)sin C
=0.
又C为△ABC的内角,
故sin C≠0,
则sin A+cos A=0,即tan A=-1.
又A∈(0,π),所以A=.
- 9 -
从而sin C=sin A=×=.
由A=知C为锐角,故C=.
答案:B
7.已知各项均为正项的等比数列{an},a1>1,0
1,0,则n的最小值为6
D.若am+an=a2+a10,则m+n>13
解析:由已知可得:an=4n-3,Sn=2n2-n,
=2n-1,则数列为等差数列,则前10项和为=100.所以A项正确;
a1,a3,am成等比数列,则a=a1·am,am=81,即am=4m-3=81,解得m=21,故B项正确;
因为=
所以=(1-+-+…+-)=>,解得n>6,故n的最小值为7,故C项错误;
等差的性质可知m+n=12,
m+n<13,故D项错误.
答案:AB
10.国家为了加强对烟酒生产的宏观管理,实行征收附加税政策.现知某种酒每瓶70元,不加附加税时,每年大约产销100万瓶,若政府征收附加税,每销售100元要征税k元(叫做税率k%),则每年的产销量将减少10k万瓶.要使每年在此项经营中所收取附加税金不少于112万元,则k的取值范围为( )
- 9 -
A.[2,8] B.(2,8)
C.(4,8) D.(1,7)
解析:设年产销售为每年x万瓶,则销售收入每年70x万元,从中征收的税金为70x·k%万元,其中x=100-10k.由题意,得70(100-10k)k%≥112,整理得k2-10k+16≤0,解得2≤k≤8.
答案:A
11.已知不等式(x+y)≥9对任意正实数x,y恒成立,则正实数a的最小值为( )
A.8 B.6
C.4 D.2
解析:只需求(x+y)的最小值大于等于9即可,又(x+y)·=1+a·++a≥a+1+2 =a+2+1,当且仅当a·=时等号成立,所以()2+2+1≥9,即()2+2-8≥0,求得≥2或≤-4(舍去),所以a≥4,
即a的最小值为4.
答案:C
12.已知△ABC中,内角A,B,C所对边长分别为a,b,c,若A=,b=2acos B,c=1,则△ABC的面积等于( )
A. B.
C. D.
解析:由正弦定理得sin B=2sin Acos B,故tan B=2sin A=2sin =,又B∈(0,π),所以B=,又A=B=,则△ABC是正三角形,所以S△ABC=bcsin A=×1×1×=.
答案:B
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.已知0<x<6,则(6-x)·x的最大值是________.
解析:因为0<x<6,所以6-x>0,
所以(6-x)·x≤=9.
- 9 -
答案:9
14.已知x>1,y>1,且ln x,1,ln y成等差数列,则x+y的最小值为________.
解析:由已知ln x+ln y=2,
所以xy=e2,x+y≥2=2e.
当且仅当x=y=e时取“=”,
所以x+y的最小值为2e.
答案:2e
15.已知{an}是等差数列,Sn为其前n项和,n∈N+,若a3=16,S20=20,则S10的值为________.
解析:设等差数列{an}的首项为a1,公差为d,
则a3=a1+2d=16,S20=20a1+d=20,
所以
解得d=-2,a1=20.
所以S10=10a1+d=200-90=110.
答案:110
16.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=,b=2,sin B+cos B=,则角A的大小为________.
解析:由题意知,sin B+cos B=,
所以sin=,所以B=,
根据正弦定理可知=,可得=,
所以sin A=,又a0,b>0,c>0,若函数f(x)=|x+a|+|x-b|+c的最小值为2.
(1)求a+b+c的值;
(2)证明:++≥.
解:(1)因为f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)|+c=|a+b|+c=a+b+c,
当且仅当-a≤x≤b时,等号成立,
所以f(x)的最小值为a+b+c,所以a+b+c=2.
(2)由(1)可知,a+b+c=2,且a,b,c都是正数,
所以++=[(a+b)+(b+c)+(c+a)](++)=[3++(
- 9 -
+)+]≥(3+2+2+2)=.
当且仅当a=b=c=1时,取等号,
所以++≥得证.
22.(本小题满分12分)据市场分析,某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系.
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润?
(3)当月产量为多少吨时,每吨平均成本最低?最低成本是多少万元?
解:(1)y=a(x-15)2+17.5(a∈R,a≠0),
将x=10,y=20代入上式得,20=25a+17.5,
解得a=,
所以y=(x-15)2+17.5(10≤x≤25).
(2)设利润为Q(x),
则Q(x)=1.6x-y
=1.6x-
=-(x-23)2+12.9(10≤x≤25),
因为x=23∈[10,25],
所以月产量为23吨时,可获最大利润12.9万元.
(3)==x+-3≥2 -3=1.
当且仅当=,即x=20∈[10,25]时上式“=”成立.
故当月产量为20吨时,每吨平均成本最低,最低成本为1万元.
- 9 -