2018届二轮复习专题01如何破解集合间的关系类问题学案（全国通用）

2018届二轮复习专题01如何破解集合间的关系类问题学案（全国通用）

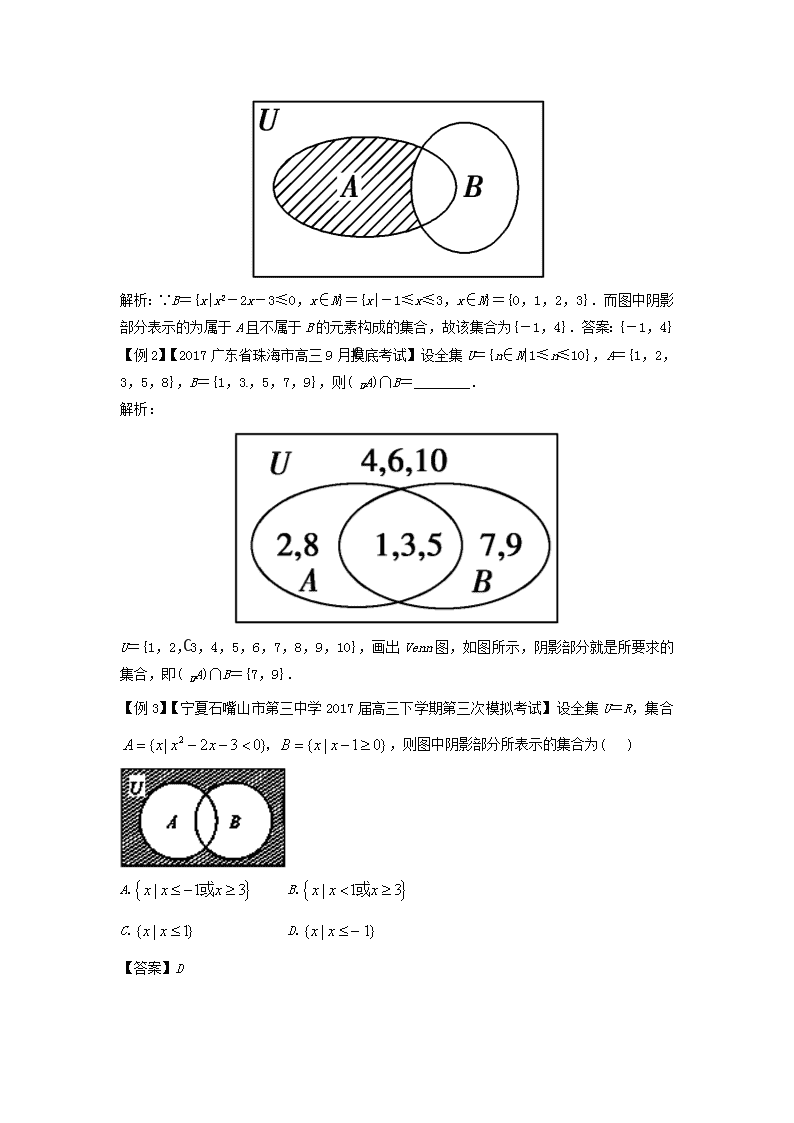
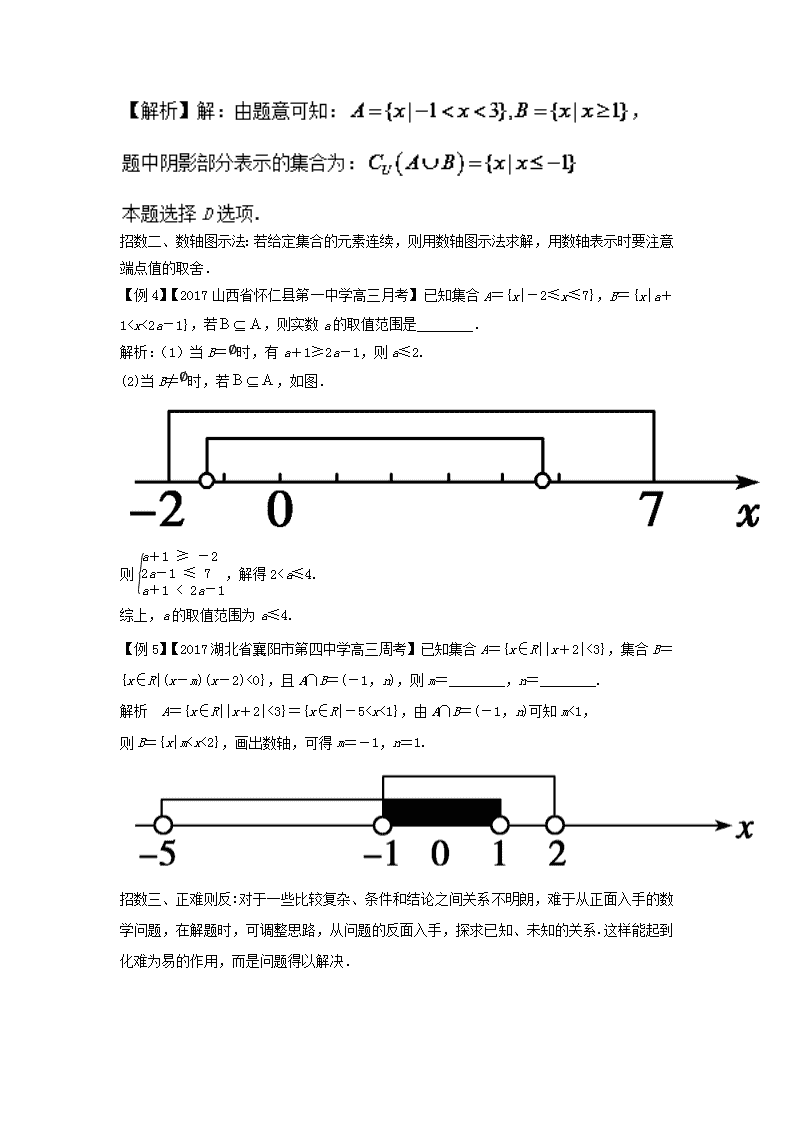
专题01 如何破解集合间的关系类问题 ‎ 考纲要求:‎ ‎1.理解集合之间包含与相等的含义，能识别给定集合的子集.‎ ‎2.在具体情境中，了解全集与空集的含义.‎ 基础知识回顾:集合与集合之间的关系 ‎1．集合间的基本关系 表示 关系　　　‎ 文字语言 符号语言 集合间的 基本关系 相等 集合A与集合B中的所有元素都相同 A＝B 子集 A中任意一个元素均为B中的元素 A⊆B 真子集 A中任意一个元素均为B中的元素，且B中至少有一个元素不是A中的元素 AB 空集 空集是任何集合的子集，是任何非空集合的真子集 ‎2.集合的基本运算 集合的并集 集合的交集 集合的补集 图形 语言 符号 语言 A∪B＝{x|x∈A，或x∈B}‎ A∩B＝{x|x∈A，且x∈B}‎ ‎∁UA＝{x|x∈U，且x∉A}‎ ‎3.集合的运算性质 并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A．‎ 交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B．‎ 补集的性质：A∪(∁UA)＝U；A∩(∁UA)＝∅；∁U(∁UA)＝A．‎ 应用举例:‎ 招数一、韦恩图:一般地，若给定的集合元素离散或者是抽象集合，则用Venn图求解．‎ ‎【例1】【2017湖南省长沙市长郡中学高三入学考试】已知集合A＝{－1，0，4}，集合B＝{x|x2－2x－3≤0，x∈N}，全集为U，则图中阴影部分表示的集合是________．‎ 解析：∵B＝{x|x2－2x－3≤0，x∈N}＝{x|－1≤x≤3，x∈N}＝{0，1，2，3}．而图中阴影部分表示的为属于A且不属于B的元素构成的集合，故该集合为{－1，4}．答案：{－1，4}‎ ‎【例2】【2017广东省珠海市高三9月摸底考试】设全集U＝{n∈N|1≤n≤10}，A＝{1，2，3，5，8}，B＝{1，3，5，7，9}，则(∁UA)∩B＝________．‎ 解析：‎ U＝{1，2，3，4，5，6，7，8，9，10}，画出Venn图，如图所示，阴影部分就是所要求的集合，即(∁UA)∩B＝{7，9}．‎ ‎【例3】【宁夏石嘴山市第三中学2017届高三下学期第三次模拟考试】设全集U＝R，集合，则图中阴影部分所表示的集合为( )‎ A. B.‎ C. D.‎ ‎【答案】D 招数二、数轴图示法：若给定集合的元素连续，则用数轴图示法求解，用数轴表示时要注意端点值的取舍．‎ ‎【例4】【2017山西省怀仁县第一中学高三月考】已知集合A＝{x|－2≤x≤7}，B＝{x|a＋10}，R是实数集，则(∁RB)∩A等于( )‎ A. B.(0,1]‎ C.(－∞，0] D.以上都不对 ‎【答案】B ‎ ‎ ‎2．【2017届福建省泉州市高三3月质量检测】已知集合，则( )‎ A. B. C. D.‎ ‎【答案】B ‎【解析】由题意得，，，则，故选B.‎ ‎3．【2017届湖南省邵阳市高三下学期第二次联考】若集合，集合，则等于( )‎ A. B. C. D.‎ ‎【答案】C ‎【解析】由题意可得，,故选C. ‎ ‎4．【陕西省西安市长安区第一中学高三4月模拟考试】已知,,若,则( )‎ A. B. C.或 D.或或 ‎【答案】D ‎ 5．【辽宁省锦州市2017届高三质量检测】集合，集合，则集合与集合的关系( )‎ A. B. C. D.且 ‎【答案】D ‎【解析】因为,所以且,选D.‎ ‎6．若集合，，则集合的子集共有( )‎ A.2个 B.4个 C.8个 D.16个 ‎【答案】D ‎【解析】集合：,集合=,则集合的子集有个.‎ 点睛：对于有限集合我们有一下结论：若一个集合中有n个元素，则它有个子集.有-1个真子集 ‎7、已知A，B均为集合U＝{1,3,5,7,9}的子集，且A∩B＝{3}，(∁UB)∩A＝{9}，则A＝(　　)‎ A．{1,3} B．{3,7,9} C．{3,5,9} D．{3,9}‎ 解析：方法一：因为A∩B＝{3}，所以3∈A，又因为 ‎(∁UB)∩A＝{9}，所以9∈A，故选D.‎ 方法二：如图8所示，得A＝{3,9}，故选D.‎ ‎8、某校田径队共30人，主要专练‎100m，‎200m与‎400m．其中练‎100m的有12人，练‎200m的有15人，只练‎400m的有8人．则参加‎100m的专练人数为________．‎ 解析：用Venn图表示A代表练‎100m的人员集合，B代表练‎200m的人员集合，C代表练‎400m的人员集合，U代表田径队共30人的集合，设既练‎100m又练‎200m的人数为x，则专练‎100m的人数为12－x.∴12－x＋15＋8＝30，解得x＝5.所以专练‎100m的人数为12－5＝7.答案：7‎ ‎9、【2017江苏泰兴中学高三月考】已知集合A＝{x|1<2x≤16}，B＝{x|x

查看更多