宁夏石嘴山市第三中学2019-2020学年高二上学期期中考试数学（文）试题

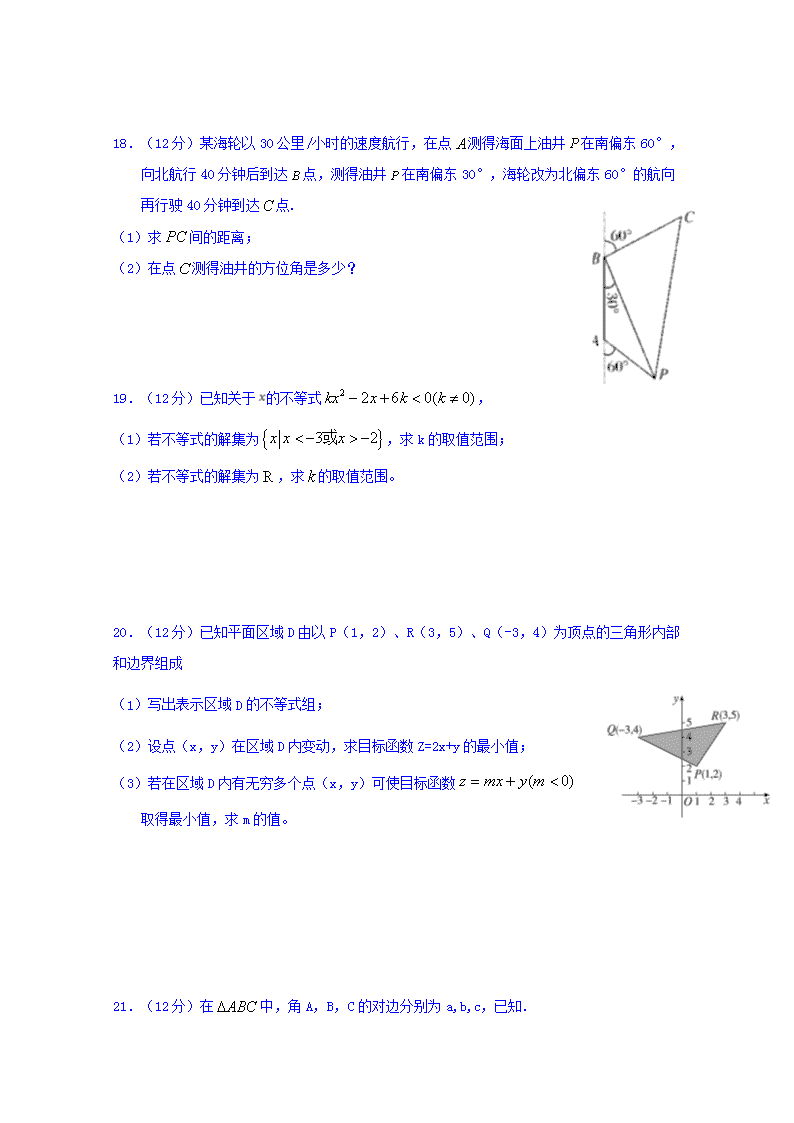
宁夏石嘴山市第三中学2019-2020学年高二上学期期中考试数学（文）试题

‎2019-2020学年高二数学（文科）期中试卷 一、单选题（每题5分，共60分）‎ ‎1．已知全集U=R，A={x|x2﹣2x＜0}，B={x|x≥1}，则A∪（∁UB）=（　　）‎ A.（0，+∞） B.（﹣∞，1） C.（﹣∞，2） D.（0，1）‎ ‎2．设，则下列不等式一定成立的是（ ）‎ A． B． C． D．‎ ‎3．已知的内角，，的对边分别为，，，若，，，则（ ）‎ A. B. C. D.‎ ‎4．不等式的解集是（ ）‎ A． B． C． D．‎ ‎5．在中，角，，的对边分别为，，，已知，则此三角形解的情况是（ ）‎ A．一解 B．两解 C．一解或两解 D．无解 ‎6．在中，，，，则的面积是（ 　 ）‎ A．　　　　 　B．　　　　 C．　　　 D．‎ ‎7．已知数列{an}满足a1＝2，an+1＝3an+2，则{an}的通项公式为（ 　 ）‎ A.an＝2n-1 B.an＝3n‎-1 ‎C.an＝2n-1 D.an＝6n-4‎ ‎8．不等式y≥|x|表示的平面区域是( )‎ ‎9．等比数列中，若，且成等差数列，则其前5项和为（ ）‎ A．30 B．‎32 ‎C．62 D．64‎ ‎10．在等差数列中，，则（ ）‎ A．17 B．‎26 C．30 D．56‎ ‎11．在中，角A ,B ,C的对边分别为a ,b ,c，若，则角B的值为（ ）‎ A. B． C． D．‎ ‎12．已知各项都为正数的等比数列，满足，若存在两项，使得，则的最小值为（ ）‎ A.2 B. C. D.1‎ 二、填空题（每题5分，共20分）‎ ‎13．若点P(m，2)不在不等式x＋4y－1＞0表示的平面区域内，则m满足的条件是__________．‎ ‎14．函数的最小值为__________．‎ ‎15.已知等差数列共有项，所有奇数项之和为，所有偶数项之和为，则n等于____________．‎ ‎16.已知f(x)＝x2＋2(a－2)x＋4，如果对x∈[－3，1]，f(x)＞0恒成立，则实数a的取值范围为________．‎ 三、解答题 ‎17．（10分）(1)为等差数列的前项和，,，求.‎ ‎(2)在等比数列中，若求首项和公比.‎ ‎18．（12分）某海轮以30公里/小时的速度航行，在点测得海面上油井在南偏东60°，向北航行40分钟后到达点，测得油井在南偏东30°，海轮改为北偏东60°的航向再行驶40分钟到达点.‎ ‎（1）求间的距离；‎ ‎（2）在点测得油井的方位角是多少？‎ ‎19．（12分）已知关于的不等式，‎ ‎（1）若不等式的解集为，求k的取值范围；‎ ‎（2）若不等式的解集为，求的取值范围。‎ ‎20．（12分）已知平面区域D由以P（1，2）、R（3，5）、Q（-3，4）为顶点的三角形内部和边界组成 ‎（1）写出表示区域D的不等式组；‎ ‎（2）设点（x，y）在区域D内变动，求目标函数Z=2x+y的最小值；‎ ‎（3）若在区域D内有无穷多个点（x，y）可使目标函数 取得最小值，求m的值。‎ ‎21．（12分）在中，角A，B，C的对边分别为a,b,c，已知.‎ ‎（1）求角A 的大小；‎ ‎（2）若 ，面积为 ，试判断的形状，并说明理由.‎ ‎22．（12分）已知数列满足，又等差数列满足且，，成等比数列.‎ ‎（1）求数列和的通项公式；‎ ‎（2）求数列的前项和.‎ 参考答案 ‎1．C2．D3．A4．D5．B6．C7．B8．A9．C10．C11．C12．B ‎13．(－∞，－7]‎ ‎14．5‎ ‎15．10‎ ‎16（﹣，4）‎ ‎17．（1）；（2）首项,公比 ‎【详解】‎ ‎（1）由题意可得：根据等差数列的性质可得：‎ ‎（2）在等比数列中,，,可得,‎ 而,可得.又知,.‎ 首项,公比。‎ ‎18．（1）；（2）正南40海里处 .‎ ‎【解析】：（1）在中，根据正弦定理，求，再利用余弦定理算出的长，即可算出两地间的距离；（2）根据内错角相等可证明，从而可得出结论.‎ 试题解析：（1）如图，在中，,‎ 根据正弦定理得：,‎ 在中，，‎ 由已知，‎ ‎（2）在中，，所以，所以 因为,所以,‎ 所以点测得油井在的正南40海里处.‎ ‎19．(1) ;(2) .‎ ‎【解析】 (1)利用不等式的解集确定方程的两根，然后利用根与系数的关系求得实数k的值即可；‎ ‎(2)利用题意得到关于实数k的不等式组，求解不等式组可得的取值范围是.‎ 试题解析：‎ ‎（1）因为不等式的解集为，‎ 所以是方程的两根，所以. ‎ ‎(2)若不等式的解集为，即恒成立，‎ 则满足 ‎ ‎20．，‎ 解：（1）首先求三直线PQ、QR、RP的方程.‎ 易得直线PQ的方程为x+2y-5=0;直线QR的方程为x-6y+27=0;‎ 直线RP的方程为3x-2y+1=0. ……………………………………………… 3分 注意到△PQR内任一点(x,y)应在直线RP、PQ的上方,而在QR的下方,故应有 ‎ ……………………………………………… 5分 ‎（2）由已知得直线：，取最小值时，此直线的 纵截距最小。作直线，将直线沿区域D平行移动，‎ 过点Q 时Z有最小值，………………………………… 8分 所以；…………………………………………… 9分 ‎（3）直线的斜率为-m，……………………………………… 10分 结合可行域可知，直线与直线PR重合时，线段PR上任意一点都可使 取得最小值，………………………… 12分 又,因此，，即……………………………………………… 14分 ‎21．（1） ；（2）为等边三角形．‎ ‎【详解】‎ ‎（1）由（2b﹣c）cosA﹣acosC＝0及正弦定理，得（2sinB﹣sinC）cosA﹣sinAcosC＝0，‎ ‎∴2sinBcosA﹣cos（A+C）＝0，sinB（2cosA﹣1）＝0．‎ ‎∵0＜B＜π，∴sinB≠0，∴cosA＝．∵0＜A＜π，‎ ‎∴A＝．‎ ‎（2）△ABC为等边三角形，∵S△ABC＝bcsinA＝，‎ 即bcsin＝，∴bc＝3，①‎ ‎∵a2＝b2+c2﹣2bccosA，A＝，a＝，∴b2+c2＝6，②‎ 由①②得b＝c＝，∴△ABC为等边三角形．‎ ‎22．（1），；（2）.‎ ‎【解析】：（1）当时，，当时，易得 ，和已知等式相减可得，故而可求的通项公式，由等比数列的性质可求出的公差，即可得的通项公式；（2）利用错位相减法求前项和.‎ 试题解析：（1）由 （）①得：当时，‎ 当时， ②‎ ‎①－②得：（），∴（）又上式对也成立 ‎∴，设等差数列的公差为，由已知得：‎ ‎∴，，，由，，成等比数列，得：，解得：，∴.‎ ‎（2）由（1）知：，故：‎ ‎③‎ ‎④‎ ‎③－④得： ‎ ‎∴.‎