2020学年高一数学下册期末一元二次不等式及其解法知识梳理
高一数学下学期期末备考一元二次不等式及其解法
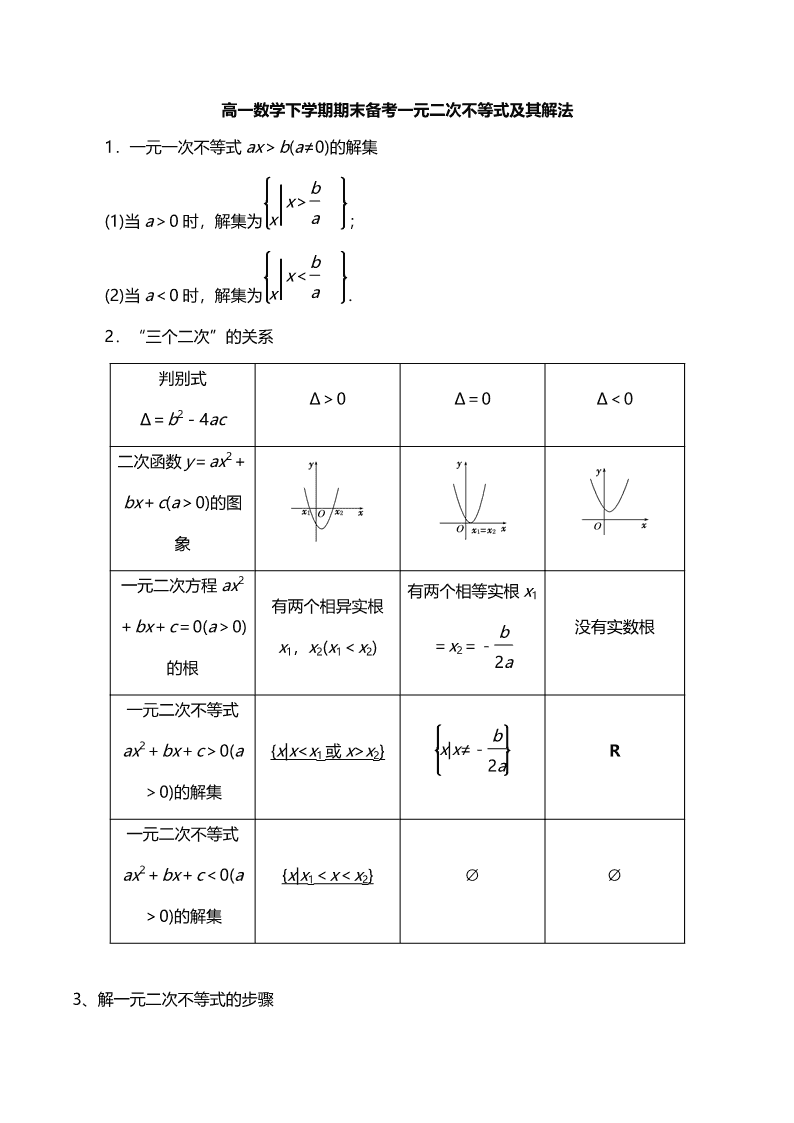
1.一元一次不等式 ax>b(a≠0)的解集
(1)当 a>0 时,解集为 x|x>
b
a ;
(2)当 a<0 时,解集为 x|x<
b
a .
2.“三个二次”的关系
判别式
Δ=b2-4ac
Δ>0 Δ=0 Δ<0
二次函数 y=ax2+
bx+c(a>0)的图
象
一元二次方程 ax2
+bx+c=0(a>0)
的根
有两个相异实根
x1,x2(x1<x2)
有两个相等实根 x1
=x2=-
b
2a
没有实数根
一元二次不等式
ax2+bx+c>0(a
>0)的解集
{x|x
x2} x|x≠-
b
2a
R
一元二次不等式
ax2+bx+c<0(a
>0)的解集
{x|x1<x<x2} ∅ ∅
3、解一元二次不等式的步骤
(1)对不等式变形,使不等号一端二次项系数大于 0,另一端为 0,即化为 ax2+bx+c>
0(a>0)或 ax2+bx+c<0(a>0)的形式;
(2)计算相应的判别式;
(3)当Δ≥0 时,求出相应的一元二次方程的根;
(4)根据对应的二次函数的图象,写出不等式的解集.
【考点精炼】
考点一:解不含参数的一元二次不等式
例 1.(全国卷Ⅲ)设集合 S={x|(x-2)(x-3)≥0},T={x|x>0},则 S∩T=( )
A.[2,3] B.(-∞,2]∪[3,+∞)
C.[3,+∞) D.(0,2]∪[3,+∞)
【答案】 D [因为 S={x|(x-2)(x-3)≥0}={x|x≥3 或 x≤2},又 T={x|x>0},所以 S∩T
=(0,2]∪[3.+∞).]
练习.(2019·广东肇庆月考)不等式-x2-3x+4>0 的解集为________.(用区间表示)
【答案】(-4,1) [由-x2-3x+4>0 得 x2+3x-4<0,解得-40 的解集为(-4,1).]
知识点
4、解含参数的一元二次不等式的步骤
(1)二次项中若含有参数应讨论是等于 0,小于 0,还是大于 0,然后将不等式转化为一次
不等式或二次项系数为正的形式.
(2)判断方程的根的个数,讨论判别式Δ与 0 的关系.
(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确
定解集形式.
考点练习
考点二、含参数的一元二次不等式问题
例 2.(2019·山东烟台检测)关于 x 的不等式 ax-b>0 的解集是(1,+∞),则关于 x 的不
等式(ax+b)(x-3)>0 的解集是( )
A.(-∞,-1)∪(3,+∞) B.(1,3)
C.(-1,3) D.(-∞,1)∪(3,+∞)
【答案】C [由题意知,a<0 且
b
a
=1,即 a=b,故不等式(ax+b)(x-3)>0 即为(x+1)(x
-3)<0,解得-1<x<3.]
练习、解不等式:ax2-(a+1)x+1<0(a>0).
解 原不等式变为(ax-1)(x-1)<0,
因为 a>0,所以 a
x-
1
a (x-1)<0.
所以当 a>1 时,解集为
1
a
1 时,不等式的解集为 x|1
a
0(a≠0)恒成立的充要条件是:a>0 且 b2-4ac<0(x∈R).
(2)ax2+bx+c<0(a≠0)恒成立的充要条件是:a<0 且 b2-4ac<0(x∈R).
7、一元二次不等式恒成立问题的求解思路
(1)形如 f(x)>0 或 f(x)<0(x∈R)的不等式确定参数的范围时,结合一元二次方程,利用判
别式来求解.
(2)形如 f(x)>0 或 f(x)<0(x∈[a,b])的不等式确定参数范围时,常转化为求二次函数的
最值或用分离参数法求最值.
(3)形如 f(x)>0 或 f(x)<0(参数 m∈[a,b])的不等式确定 x 的范围时,要注意变换主元,
一般地,知道谁的范围,就选谁当主元,求谁的范围,谁就是参数.
考点练习
考点四、形如 f(x)≥0(x∈R)求参数的范围
例 4、(2019·甘肃张掖月考)不等式(a-2)x2+2(a-2)x-4<0 对一切 x∈R 恒成立,则实
数 a 的取值范围是__________.
【答案】(-2,2] [当 a-2=0,即 a=2 时,不等式即为-4<0,对一切 x∈R 恒成立,
当 a≠2 时,则有 2
2 0
4 2 16 2 0
a
a a
即
a<2,
-23} [对任意的 k∈[-1,1],x2+(k-4)x+4-2k>0 恒成立,即
g(k)=(x-2)k+(x2-4x+4)>0,在 k∈[-1,1]时恒成立.
只需 g(-1)>0 且 g(1)>0,即
x2-5x+6>0,
x2-3x+2>0,
解得 x<1 或 x>3.]
考点七、成立问题
例 7、(2019·河南洛阳诊断)若不等式 x2+ax-2>0 在区间[1,5]上有解,则 a 的取值范
围是( )
A.
-
23
5
,+∞
B.
-
23
5
,1
C.(1,+∞) D.
-∞,-
23
5
【答案】A [由Δ=a2+8>0 知方程恒有两个不等实根,又因为 x1x2=-2<0,所以方程
必有一正根,一负根,对应二次函数图象的示意图如图.
所以不等式在区间[1,5]上有解的充要条件是 f(5)>0,解得 a>-
23
5
.]
练习、若不等式 2kx2+kx-
3
8
<0 对一切实数 x 都成立,则 k 的取值范围为( )
A.(-3,0) B.[-3,0)
C.[-3,0] D.(-3,0]
【答案】D [当 k=0 时,显然成立;当 k≠0 时,即一元二次不等式 2kx2+kx-
3
8
<0 对
一切实数 x 都成立,
则
k<0,
Δ=k2-4×2k×
-
3
8 <0,
解得-3
查看更多