- 2021-07-01 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
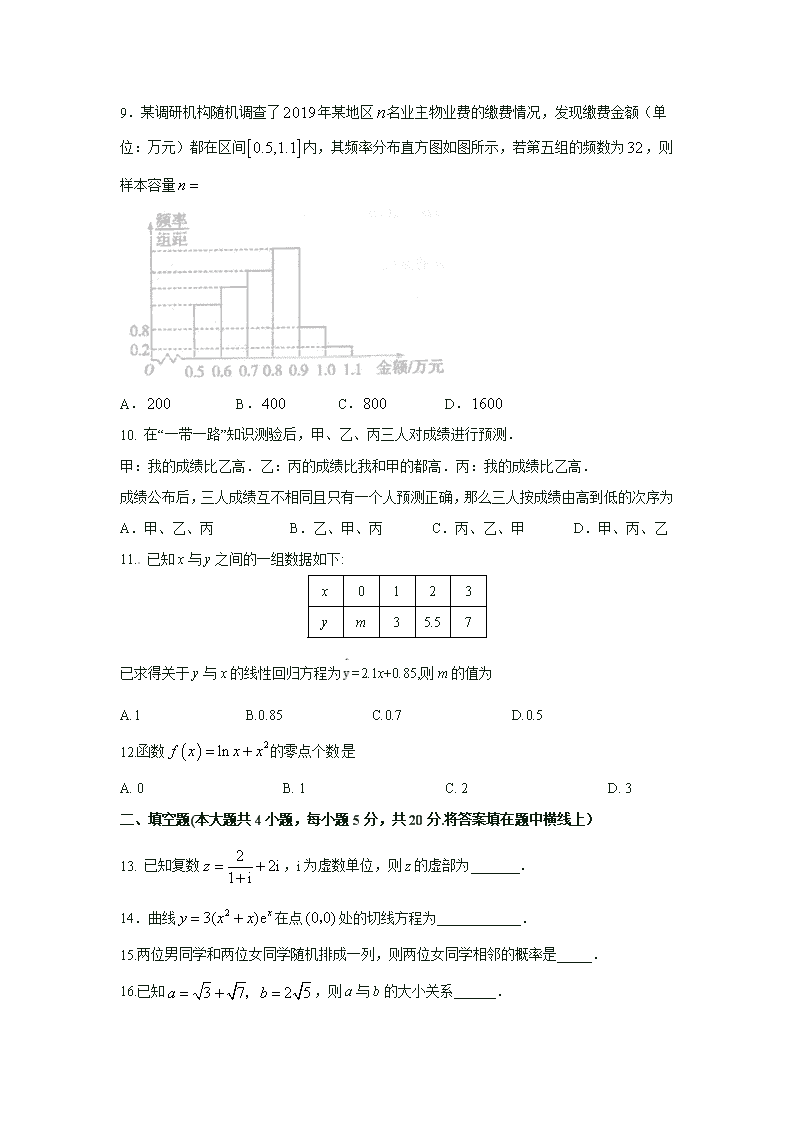
【数学】贵州省铜仁市伟才学校2019-2020学年高二下学期期中考试(文)(解析版)
贵州省铜仁市伟才学校2019-2020学年 高二下学期期中考试(文) 一、 选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只 有一项是符合题目要求的) 1 .已知集合,则 A. B. C. D. 2. A. B. C. D. 3.“”是“直线与圆相切”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 4.已知点 P(3,4) 在角的终边上,则的值为 A. B. C. D. 5.已知函数,则 A. B. C. D. 6.若,;,则实数,,的大小关系为 A. B. C. D. 7.下列求导运算正确的是 A. B. C. D. 8.下列函数中,既是偶函数,又是在区间上单调递减的函数为 A. B. C. D. 9.某调研机构随机调查了年某地区名业主物业费的缴费情况,发现缴费金额(单位:万元)都在区间内,其频率分布直方图如图所示,若第五组的频数为,则样本容量 A. B. C. D. 10. 在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测. 甲:我的成绩比乙高.乙:丙的成绩比我和甲的都高.丙:我的成绩比乙高. 成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为 A.甲、乙、丙 B.乙、甲、丙 C.丙、乙、甲 D.甲、丙、乙 11. 已知x与y之间的一组数据如下: x 0 1 2 3 y m 3 5.5 7 已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为 A.1 B.0.85 C.0.7 D.0.5 12.函数的零点个数是 A. 0 B. 1 C. 2 D. 3 二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上) 13. 已知复数,i为虚数单位,则z的虚部为 . 14.曲线在点处的切线方程为____________. 15.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是_____. 16.已知,则a与b的大小关系______. 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知复数,且为纯虚数. (1)求复数; (2)若,求复数的模. 18.(12分)求下列函数的导数. (1)y=x2sin x; (2)y=ln x+; (3)y=; 19. (12分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表: 满意 不满意 男顾客 40 10 女顾客 30 20 (1)分别估计男、女顾客对该商场服务满意的概率; (2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异? 附:. P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 20.(12分)已知函数. (I) 求的减区间; (II)当时, 求值域. 21. (12分)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表. 的分组 企业数 2 24 53 14 7 (1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例; (2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01) 附:. 22. (12分)已知函数. (Ⅰ)求曲线的斜率为1的切线方程; (Ⅱ)当时,求证:. 参考答案 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1 .已知集合,则 A. B. C. D. 【答案】D 2. A. B. C. D. 【答案】D 3.“”是“直线与圆相切”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【解析】因为直线与圆相切, 所以. 所以“”是“直线与圆相切”的充分不必要条件. 故选A 4.已知点 P(3,4) 在角的终边上,则的值为 ( ) A. B. C. D. 【详解】因为点 P(3,4) 在角的终边上,所以, , 故选:D 5.已知函数,则( ) A. B. C. D. 【解析】,故选. 6.若,;,则实数,,的大小关系为( ) A. B. C. D. 【详解】因为,,, 所以. 故选A 7.下列求导运算正确的是( ) A. B. C. D. 【详解】对A,因为,故A错;对B,,故B正确; 对C,,故C错;对D,,故D错. 所以本题选B. 8.下列函数中,既是偶函数,又是在区间上单调递减的函数为( ) A. B. C. D. 【答案】A 9..某调研机构随机调查了年某地区名业主物业费的缴费情况,发现缴费金额(单位:万元)都在区间内,其频率分布直方图如图所示,若第五组的频数为,则样本容量( ) A. B. C. D. 3.选B. 解析:根据频率分布直方图,第五组的频率为,又第五组的频数为,所以样本容量为.所以选B. 10. 在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测. 甲:我的成绩比乙高.乙:丙的成绩比我和甲的都高.丙:我的成绩比乙高. 成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为 A.甲、乙、丙 B.乙、甲、丙 C.丙、乙、甲 D.甲、丙、乙 【答案】A 11. 已知x与y之间的一组数据如下: x 0 1 2 3 y m 3 5.5 7 已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为( ). A.1 B.0.85 C.0.7 D.0.5 【解析】由题中数据,得=(0+1+2+3)=1.5, =(m+3+5.5+7)=, 故样本点的中心为. 由样本点的中心必在回归直线上可知, =2.1×1.5+0.85,解得m=0.5. 【答案】D 12.函数的零点个数是( ) A. 0 B. 1 C. 2 D. 3 【详解】因为与均在上为增函数,所以函数至多一个零点 又,,,即函数在上有一个零点 或数形结合 答案选B 二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上) 13. 已知复数,i为虚数单位,则z的虚部为 . 答案:1 解析:. 14.曲线在点处的切线方程为____________. 【答案】 【解析】所以切线的斜率, 则曲线在点处的切线方程为,即. 15.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是_____. 【答案】 16.已知,则a与b的大小关系______. 【答案】a<b 【详解】解:因为,, 所以, 因为, 所以, 而, 所以得到. 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知复数,且为纯虚数. (1)求复数; (2)若,求复数的模. 【解析】 ∵是纯虚数 ∴,且 ∴,∴ ∴ 18.(12分)求下列函数的导数. (1)y=x2sin x; (2)y=ln x+; (3)y=; 解:(1)y′=(x2)′sin x+x2(sin x)′=2xsin x+x2cos x. (2)y′=′=(ln x)′+′=-. (3)y′=′==-. 19. (12分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表: 满意 不满意 男顾客 40 10 女顾客 30 20 (1)分别估计男、女顾客对该商场服务满意的概率; (2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异? 附:. P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 解:(1)由调查数据,男顾客中对该商场服务满意的比率为,因此男顾客对该商场服务满意的概率的估计值为0.8. 女顾客中对该商场服务满意的比率为,因此女顾客对该商场服务满意的概率的估计值为0.6. (2). 由于,故有95%的把握认为男、女顾客对该商场服务的评价有差异. 20.(12分)已知函数. (I) 求的减区间; (II)当时, 求值域. 【答案】(I) (II) 【详解】解: (I) 由函数, 求导 当, 解得 即的减区间 (II) 当, 解得 即在上递减, 在上递增 故的值域 21. (12分)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表. 的分组 企业数 2 24 53 14 7 (1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例; (2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01) 附:. 解:(1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为. 产值负增长的企业频率为. 用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%. (2), , , 所以,这类企业产值增长率的平均数与标准差的估计值分别为0.30,. 22. (12分)已知函数. (Ⅰ)求曲线的斜率为1的切线方程; (Ⅱ)当时,求证:; 解:(Ⅰ)由得. 令,即,得或. 又,, 所以曲线的斜率为1的切线方程是与, 即与. (Ⅱ)令. 由得. 令得或. 的情况如下: [来源:Z#xx#k.Com] 所以的最小值为,最大值为. 故,即.查看更多