山西省朔州市怀仁某校2018-2019学年高二上学期第四次月考数学（文）试卷

山西省朔州市怀仁某校2018-2019学年高二上学期第四次月考数学（文）试卷

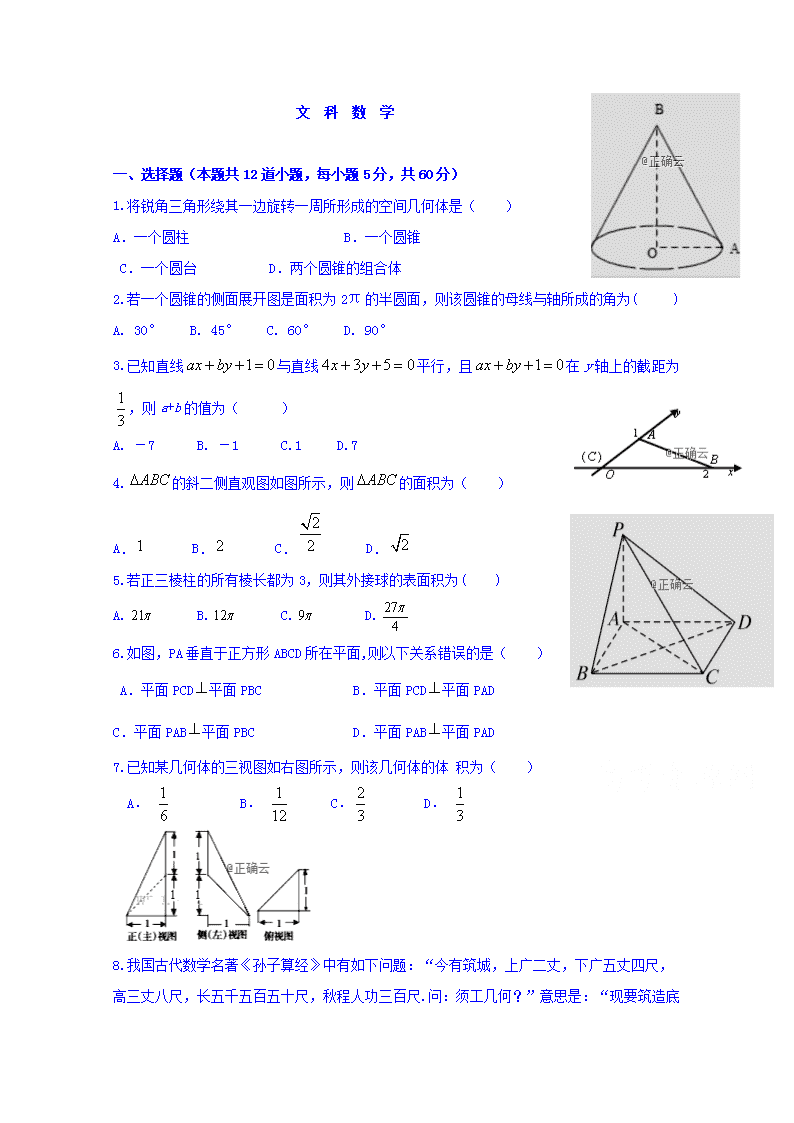
文 科 数 学 ‎ ‎ 一、选择题（本题共12道小题，每小题5分，共60分）‎ ‎1.将锐角三角形绕其一边旋转一周所形成的空间几何体是（ ）‎ A．一个圆柱 B．一个圆锥 ‎ ‎ C．一个圆台 D．两个圆锥的组合体 ‎ ‎2.若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的母线与轴所成的角为( )‎ A. 30° B. 45° C. 60° D. 90°‎ ‎3.已知直线与直线平行，且在y轴上的截距为，则a+b的值为（ ）‎ A. －7 B. －1 C.1 D.7‎ ‎4.的斜二侧直观图如图所示，则的面积为（ ）‎ A． B． C． D．‎ ‎5.若正三棱柱的所有棱长都为3，则其外接球的表面积为( )‎ A. B. C. D.‎ ‎6.如图，PA垂直于正方形ABCD所在平面,则以下关系错误的是（　　）‎ ‎ A．平面PCD平面PBC　　　　　 B．平面PCD平面PAD C．平面PAB平面PBC　　　　 D．平面PAB平面PAD ‎7.已知某几何体的三视图如右图所示，则该几何体的体 积为（ ）‎ ‎ A． B． C． D． ‎ ‎8.‎ 我国古代数学名著《孙子算经》中有如下问题：“今有筑城，上广二丈，下广五丈四尺，高三丈八尺，长五千五百五十尺，秋程人功三百尺.问：须工几何？”意思是：“现要筑造底面为等腰梯形的直棱柱的城墙，其中底面等腰梯形的上底为2丈、下底为5.4丈、高为3.8丈，直棱柱的侧棱长为5550尺.如果一个秋天工期的单个人可以筑出300立方尺，问：一个秋天工期需要多少个人才能筑起这个城墙？”（注：一丈等于十尺）（ ）‎ A．24642 B．26011 C.52022 D．78033‎ ‎9.已知，是空间中两条不同的直线，，是两个不同的平面，则下列说法正确的是（ ）‎ A．若，，，则 B．若，，则 C. 若，，则 D．若，，，且，，则 ‎10.某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A 54 B 60 C 66 D 7211.直线xcos α＋y＋2＝0的倾斜角的范围是 (　　) ‎ A. [,)∪(,]B. [0,]∪[,π) C. [0,] D. [ ,]‎ ‎12．在棱长为1的正方体ABCD﹣A1B1C1D1中，AC∩BD=O，E是线段B1C（含端点）上的一动点，则 ‎①OE⊥BD1； ②OE∥面A1C1D；‎ ‎③三棱锥A1﹣BDE的体积为定值；④OE与A1C1所成的最大角为90°．‎ 上述命题中正确的个数是（　　）‎ A．1 B．2 C．3 D．4‎ 二、 填空题（本题共4道小题，每小题5分，共20分）‎ ‎13.已知A（1，3），B（a，1），C（﹣b，0），（a＞0，b＞0），若A，B，C三点共线，则 +的最小值是　 　．‎ ‎14.已知两点A（﹣2，0），B（0，2），点C是圆x2+y2﹣2x=0上的任意一点，则△ABC的面积最小值是　 　．‎ ‎15.已知正三棱锥P - ABC的体积为，其外接球球心为O，且满足，则正三棱锥P - ABC的外接球半径为 ．‎ ‎16.已知棱长为1的正方体中，，，分别是线段、、的中点，又、分别在线段、上，且．‎ 设平面∩平面，现有下列结论：‎ ‎①∥平面；②⊥；‎ ‎③直线与平面不垂直；④当变化时，不是定直线．‎ 其中成立的结论是_____．(写出所有成立结论的序号)‎ 二、 解答题 ‎17.（本小题10分）已知直线l：x+y﹣1=0，‎ ‎（1）若直线l1过点（3，2）且l1∥l，求直线l1的方程；‎ ‎（2）若直线l2过l与直线2x﹣y+7=0的交点，且l2⊥l，求直线l2的方程．‎ ‎18.（本小题12分）‎ 如图，四棱锥P-ABCD的底面ABCD是菱形，∠BCD=60°， PA⊥平面ABCD，E是AB的中点，F是PC的中点．‎ ‎（1）求证：平面PDE⊥平面PAB．‎ ‎（2）求证：BF∥平面PDE．‎ ‎19.（本小题12分）‎ 设直线l的方程为（a+1）x+y+2﹣a=0（a∈R）．‎ ‎（1）若l在两坐标轴上的截距相等，求l的方程；‎ ‎（2）若l不经过第二象限，求实数a的取值范围．‎ ‎20.（本小题12分）‎ 已知四棱锥P - ABCD中，底面ABCD是边长为2的正方形，，，E为CD的中点.‎ ‎（1）求证：PD⊥平面PAB；‎ ‎（2）求三棱锥P - ABE的体积.‎ ‎21（本小题12分）.已知圆M过两点C(1,-1),D(-1,1),且圆心M在x+y-2=0上.‎ ‎(1)求圆M的方程.‎ ‎(2)设P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.‎ ‎22.(本小题满分12分)‎ 如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF∥AB，AB=2，BC=EF=1，AE=，DE=3，∠BAD=60°，G为BC的中点.‎ ‎(Ⅰ)求证：FG∥平面BED；‎ ‎(Ⅱ)求证：平面BED⊥平面AED；‎ ‎(Ⅲ)求直线EF与平面BED所成角的正弦值.‎ 高二文科数学月考四答案 ‎1.D 2.A 3.A 4.B 5.A 6.A 7.A 8.B 9.B 10.B 11.B 12.D ‎【解答】解：①利用BD1⊥平面AB1C，可得OE⊥BD1，正确；‎ ‎②利用平面AB1C∥面A1C1D，可得OE∥面A1C1D，正确；‎ ‎③三棱锥A1﹣BDE的体积=三棱锥E﹣A1BD的体积，底面为定值，E到平面的距离A1BD为定值，∴三棱锥A1﹣BDE的体积为定值，正确；‎ ‎④E在B1处O，E与A1C1所成的最大角为90°，正确．‎ 故选D．‎ ‎13.11+6 14. 15. 16.①②③ ‎ 解:连接BD，B1D1，∵A1P＝A1Q＝x，‎ ‎∴PQ∥B1D1∥BD∥EF，易证PQ∥平面MEF，‎ 又平面MEF∩平面MPQ=l，∴PQ∥l，l∥EF，‎ ‎∴l∥平面ABCD，故①成立；‎ 又EF⊥AC，∴l⊥AC，故②成立；‎ ‎∵l∥EF∥BD，∴易知直线l与平面BCC1B1不垂直，‎ 故③成立； 当x变化时，l是过点M且与直线EF平行的定直线，故④不成立．‎ ‎17.解：（1）由题意和平行关系设直线l1的方程为x+y+m=0，‎ ‎∵直线l1过点（3，2），∴3+2+m=0，‎ 解得m=﹣5，直线l1的方程为x+y﹣5=0；‎ ‎（2）解方程组可得，‎ ‎∴直线l与直线2x﹣y+7=0的交点为（﹣2，3）‎ ‎∵l2⊥l，∴直线l2的斜率k=1，‎ ‎∴直线方程为x﹣y+5=0‎ ‎18（）∵底面是菱形，，‎ ‎∴为正三角形，‎ 是的中点，，‎ 平面，平面，‎ ‎∴，‎ ‎∵，‎ ‎∴平面，‎ ‎∵平面，‎ ‎∴平面平面．‎ ‎（）取的中点，连结，，‎ ‎∵，是中点，‎ ‎∴且，‎ ‎∴与平行且相等，‎ ‎∴，‎ ‎∵平面，平面，‎ ‎∴平面．‎ ‎19.解：（1）令x=0，得y=a﹣2． 令y=0，得（a≠﹣1）．‎ ‎∵l在两坐标轴上的截距相等，∴，解之，得a=2或a=0．‎ ‎∴所求的直线l方程为3x+y=0或x+y+2=0．‎ ‎（2）直线l的方程可化为 y=﹣（a+1）x+a﹣2．∵l不过第二象限，‎ ‎∴，∴a≤﹣1．∴a的取值范围为（﹣∞，﹣1]．‎ ‎20.（1）∵底面是正方形，∴，又，‎ ‎∴，‎ ‎∵，，∴，‎ ‎∴，又，∴平面.‎ ‎（2）∵，且，∴平面，‎ 又平面，∴平面平面，‎ 过作于，则平面，‎ ‎∴为三棱锥的高，∴.‎ ‎21.(1)设圆M的方程为:(x-a)2+(y-b)2=r2(r>0).‎ 根据题意,得 解得a=b=1,r=2,故所求圆M的方程为(x-1)2+(y-1)2=4.‎ ‎(2)因为四边形PAMB的面积S=S△PAM+S△PBM=|AM|·|PA|+|BM|·|PB|,‎ 又|AM|=|BM|=2,|PA|=|PB|,所以S=2|PA|,‎ 而|PA|==,‎ 即S=2.‎ 因此要求S的最小值,只需求|PM|的最小值即可,‎ 即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,‎ 所以|PM|min==3,‎ 所以四边形PAMB面积的最小值为 S=2=2=2.‎ ‎22.（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）‎ ‎（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面平面.‎ ‎（Ⅲ）解：因为，所以直线与平面所成角即为直线与平面所成角.过点作于点，连接，又因为平面平面，由（Ⅱ）知平面，所以直线与平面所成角即为.在中，，由余弦定理可得，所以，因此，在中，，所以直线与平面所成角的正弦值为.‎