【数学】2020届一轮复习人教B版任意角弧度制及任意角的三角函数学案

【数学】2020届一轮复习人教B版任意角弧度制及任意角的三角函数学案

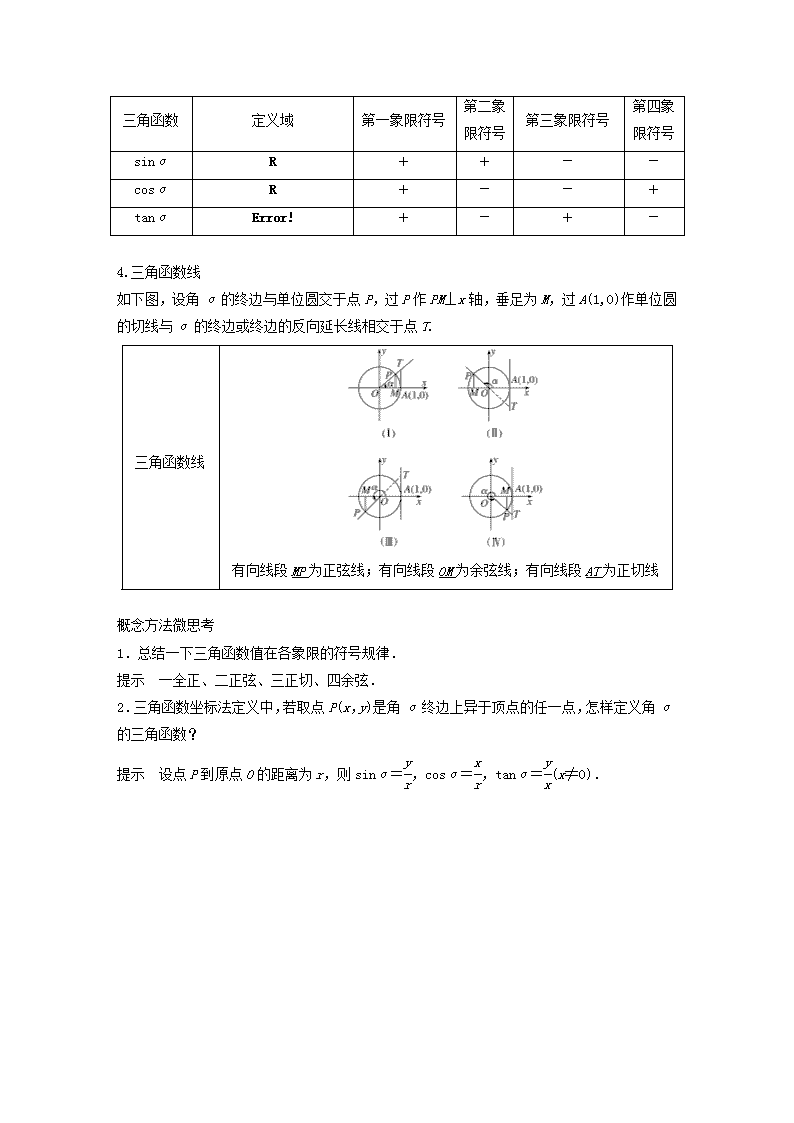
‎§5.1　任意角、弧度制及任意角的三角函数 最新考纲 考情考向分析 ‎1.了解角、角度制与弧度制的概念，掌握弧度与角度的换算．‎ ‎2.理解正弦函数、余弦函数、正切函数的定义.‎ 以理解任意角三角函数的概念、能进行弧度与角度的互化和扇形弧长、面积的计算为主，常与向量、三角恒等变换相结合，考查三角函数定义的应用及三角函数的化简与求值，考查分类讨论思想和数形结合思想的应用意识．题型以选择题为主，低档难度.‎ ‎1．角的概念 ‎(1)任意角：①定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形；②分类：角按旋转方向分为正角、负角和零角．‎ ‎(2)所有与角α终边相同的角，连同角α在内，构成的角的集合是S＝{β|β＝k·360°＋α，k∈Z}．‎ ‎(3)象限角：使角的顶点与原点重合，角的始边与x轴的非负半轴重合，那么，角的终边在第几象限，就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．‎ ‎2．弧度制 ‎(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度．正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0.‎ ‎(2)角度制和弧度制的互化：180°＝πrad,1°＝rad，1rad＝°.‎ ‎(3)扇形的弧长公式：l＝|α|·r，扇形的面积公式：S＝lr＝|α|·r2.‎ ‎3．任意角的三角函数 任意角α的终边与单位圆交于点P(x，y)时，‎ 则sinα＝y，cosα＝x，tanα＝(x≠0)．‎ 三个三角函数的初步性质如下表：‎ 三角函数 定义域 第一象限符号 第三象限符号 第二象限符号 第四象限符号 sinα R ‎＋‎ ‎＋‎ ‎－‎ ‎－‎ cosα R ‎＋‎ ‎－‎ ‎－‎ ‎＋‎ tanα ‎＋‎ ‎－‎ ‎＋‎ ‎－‎ ‎4.三角函数线 如下图，设角α的终边与单位圆交于点P，过P作PM⊥x轴，垂足为M，过A(1,0)作单位圆的切线与α的终边或终边的反向延长线相交于点T.‎ 三角函数线 有向线段MP为正弦线；有向线段OM为余弦线；有向线段AT为正切线 概念方法微思考 ‎1．总结一下三角函数值在各象限的符号规律．‎ 提示　一全正、二正弦、三正切、四余弦．‎ ‎2．三角函数坐标法定义中，若取点P(x，y)是角α终边上异于顶点的任一点，怎样定义角α的三角函数？‎ 提示　设点P到原点O的距离为r，则sinα＝，cosα＝，tanα＝(x≠0)．‎ 题组一　思考辨析 ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)锐角是第一象限的角，第一象限的角也都是锐角．(　×　)‎ ‎(2)角α的三角函数值与其终边上点P的位置无关．(　√　)‎ ‎(3)不相等的角终边一定不相同．(　×　)‎ ‎(4)若α为第一象限角，则sinα＋cosα>1.(　√　)‎ 题组二　教材改编 ‎2．[P10A组T7]角－225°＝______弧度，这个角在第______象限．‎ 答案　－　二 ‎3．[P15T2]若角α的终边经过点Q，则sinα＝____，cosα＝________.‎ 答案　　－ ‎4．[P10A组T6]一条弦的长等于半径，这条弦所对的圆心角大小为____弧度．‎ 答案　 题组三　易错自纠 ‎5．集合中的角所表示的范围(阴影部分)是(　　)‎ 答案　C 解析　当k＝2n(n∈Z)时，2nπ＋≤α≤2nπ＋，此时α表示的范围与≤α≤表示的范围一样；当k＝2n＋1 (n∈Z)时，2nπ＋π＋≤α≤2nπ＋π＋，此时α表示的范围与π＋≤α≤π＋表示的范围一样，故选C.‎ ‎6．已知点P在角θ的终边上，且θ∈[0,2π)，则θ的值为(　　)‎ A.B.C.D. 答案　C 解析　因为点P在第四象限，所以根据三角函数的定义可知tanθ＝＝－，又θ∈，所以θ＝.‎ ‎7．在0到2π范围内，与角－终边相同的角是________．‎ 答案　 解析　与角－终边相同的角是2kπ＋(k∈Z)，令k＝1，可得与角－终边相同的角是.‎ ‎8．函数y＝的定义域为__________________．‎ 答案　(k∈Z)‎ 解析　∵2cosx－1≥0，∴cosx≥.‎ 由三角函数线画出x满足条件的终边范围(如图阴影部分所示)，‎ ‎∴x∈(k∈Z)．‎ 题型一　角及其表示 ‎1．下列与角的终边相同的角的表达式中正确的是 (　　)‎ A．2kπ＋45°(k∈Z) B．k·360°＋(k∈Z)‎ C．k·360°－315°(k∈Z) D．kπ＋(k∈Z)‎ 答案　C 解析　与角的终边相同的角可以写成2kπ＋(k∈Z)，但是角度制与弧度制不能混用，所以只有答案C正确．‎ ‎2．设集合M＝，N＝，那么(　　)‎ A．M＝NB．M⊆NC．N⊆MD．M∩N＝∅‎ 答案　B 解析　由于M中，x＝·180°＋45°＝k·90°＋45°＝(2k＋1)·45°，2k＋1是奇数；而N中，x＝·180°＋45°＝k·45°＋45°＝(k＋1)·45°，k＋1是整数，因此必有M⊆N，故选B.‎ ‎3．终边在直线y＝x上，且在[－2π，2π)内的角α的集合为______________________．‎ 答案　 解析　如图，在坐标系中画出直线y＝x，可以发现它与x轴的夹角是，在[0,2π)内，终边在直线y＝x上的角有两个：，π；‎ 在[－2π，0)内满足条件的角有两个：－π，－π，故满足条件的角α构成的集合为.‎ ‎4．若角α是第二象限角，则是第________象限角．‎ 答案　一或三 解析　∵α是第二象限角，‎ ‎∴＋2kπ<α<π＋2kπ，k∈Z，‎ ‎∴＋kπ<<＋kπ，k∈Z.当k为偶数时，是第一象限角；当k为奇数时，是第三象限角．‎ 综上，是第一或第三象限角．‎ 思维升华 (1)利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k(k∈Z)赋值来求得所需的角．‎ ‎(2)确定kα，(k∈N*)的终边位置的方法 先写出kα或的范围，然后根据k的可能取值确定kα或的终边所在位置．‎ 题型二　弧度制及其应用 例1已知一扇形的圆心角为α，半径为R，弧长为l.若α＝，R＝10cm，求扇形的面积．‎ 解　由已知得α＝，R＝10cm，‎ ‎∴S扇形＝α·R2＝··102＝(cm2)．‎ 引申探究 ‎1．若例题条件不变，求扇形的弧长及该弧所在弓形的面积．‎ 解　l＝α·R＝×10＝(cm)，‎ S弓形＝S扇形－S三角形 ‎＝·l·R－·R2·sin ‎＝··10－·102·＝(cm2)．‎ ‎2．若例题条件改为：“若扇形周长为20cm”，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？‎ 解　由已知得，l＋2R＝20，则l＝20－2R(00.则实数a的取值范围是(　　)‎ A．(－2,3] B．(－2,3)‎ C．[－2,3) D．[－2,3]‎ 答案　A 解析　∵cosα≤0，sinα>0，‎ ‎∴角α的终边落在第二象限或y轴的正半轴上．‎ ‎∴　∴－2cosx成立的x的取值范围是(　　)‎ A.∪ B. C. D.∪ 答案　C 解析　当x∈时，sinx>0，cosx≤0，显然sinx>cosx成立；当x∈时，如图，OA为x的终边，此时sinx＝|MA|，cosx＝|OM|，sinx≤cosx；当x∈时，如图，‎ OB为x的终边，此时sinx＝|NB|，cosx＝|ON|，sinx>cosx．同理当x∈ 时，sinx>cosx；当x∈时，sinx≤cosx，故选C.‎ ‎1．下列说法中正确的是(　　)‎ A．第一象限角一定不是负角 B．不相等的角，它们的终边必不相同 C．钝角一定是第二象限角 D．终边与始边均相同的两个角一定相等 答案　C 解析　因为－330°＝－360°＋30°，所以－330°角是第一象限角，且是负角，所以A错误；同理－330°角和30°角不相等，但它们终边相同，所以B错误；因为钝角的取值范围为(90°，180°)，所以C正确；0°角和360°角的终边与始边均相同，但它们不相等，所以D错误．‎ ‎2．已知扇形的周长是6，面积是2，则扇形的圆心角的弧度数是(　　)‎ A．1B．4C．1或4D．2或4‎ 答案　C 解析　设扇形的半径为r，弧长为l，‎ 则解得或 从而α＝＝＝4或α＝＝＝1.‎ ‎3．若角θ终边过点P(4，m)，且sinθ＝，则m等于(　　)‎ A．－3B．3C.D．±3‎ 答案　B 解析　sinθ＝＝，且m>0，解得m＝3.‎ ‎4．点P从(1,0)出发，沿单位圆逆时针方向运动弧长到达Q点，则Q点的坐标为(　　)‎ A. B. C. D. 答案　A 解析　点P旋转的弧度数也为，由三角函数定义可知Q点的坐标(x，y)满足x＝cos＝‎ ‎－，y＝sin＝.‎ ‎5．已知点P(cosα，tanα)在第二象限，则角α的终边在(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案　C 解析　因为点P(cosα，tanα)在第二象限，‎ 所以所以角α的终边在第三象限，故选C.‎ ‎6．(2018·嘉兴模拟)sin2·cos3·tan4的值(　　)‎ A．小于0 B．大于0‎ C．等于0 D．不存在 答案　A 解析　∵sin2>0，cos3<0，tan4>0，‎ ‎∴sin2·cos3·tan4<0.‎ ‎7．已知角α的终边过点P(－8m，－6sin30°)，且cosα＝－，则m的值为(　　)‎ A．－ B．－ C. D. 答案　C 解析　由题意得点P(－8m，－3)，r＝，‎ 所以cosα＝＝－，解得m＝±，‎ 又cosα＝－<0，所以－8m<0，即m>0，‎ 所以m＝.‎ ‎8．下列命题中正确命题的个数是(　　)‎ ‎①第二象限角大于第一象限角；‎ ‎②三角形的内角是第一象限角或第二象限角；‎ ‎③不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；‎ ‎④若sinα＝sinβ，则α与β的终边相同；‎ ‎⑤若cosθ<0，则θ是第二或第三象限的角．‎ A．1B．2C．3D．4‎ 答案　A 解析　举反例：第一象限角370°不小于第二象限角100°，故①错；当三角形的内角为90°时，其既不是第一象限角，也不是第二象限角，故②错；③正确；由于sin＝sin，但与的终边不相同，故④错；当cosθ＝－1，θ＝π时，其既不是第二象限角，也不是第三象限角，故⑤错．‎ 综上可知，只有③正确．‎ ‎9．若圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是________．‎ 答案　 解析　设圆半径为r，则圆内接正方形的对角线长为2r，∴正方形边长为r，∴圆心角的弧度数是＝.‎ ‎10．若角α的终边与直线y＝3x重合，且sinα<0，又P(m，n)是角α终边上一点，且|OP|＝，则m－n＝________.‎ 答案　2‎ 解析　由已知tanα＝3，∴n＝3m，‎ 又m2＋n2＝10，∴m2＝1.‎ 又sinα<0，∴m＝－1，n＝－3.故m－n＝2.‎ ‎11．已知角α的终边上一点P的坐标为，则角α的最小正值为________．‎ 答案　 解析　由题意知，点P，r＝1，所以点P在第四象限，根据三角函数的定义得cosα＝sin＝，故α＝2kπ－(k∈Z)，所以α的最小正值为.‎ ‎12．函数y＝的定义域为__________________．‎ 答案　，k∈Z 解析　利用三角函数线(如图)，‎ 由sinx≥，可知 ‎2kπ＋≤x≤2kπ＋π，k∈Z.‎ ‎13.已知角α的终边在如图所示阴影表示的范围内(不包括边界)，则角α用集合可表示为________________．‎ 答案　 解析　∵在[0,2π)内，终边落在阴影部分角的集合为 ，‎ ‎∴所求角的集合为.‎ ‎14．若角α的终边落在直线y＝x上，角β的终边与单位圆交于点，且sinα·cosβ<0，则cosα·sinβ＝________.‎ 答案　± 解析　由角β的终边与单位圆交于点，得cosβ＝，又由sinα·cosβ<0知，sinα<0，因为角α的终边落在直线y＝x上，所以角α只能是第三象限角．记P为角α的终边与单位圆的交点，设P(x，y)(x<0，y<0)，则|OP|＝1(O为坐标原点)，即x2＋y2＝1，又由y＝x得x＝－，y＝－，所以cosα＝x＝－，因为点在单位圆上，所以2＋m2＝1，解得m＝±，所以sinβ＝±，所以cosα·sinβ＝±.‎ ‎15．《九章算术》是我国古代数学成就的杰出代表作，其中“方田”章给出了计算弧田面积时所用的经验公式，即弧田面积＝×(弦×矢＋矢2)．弧田(如图1)由圆弧和其所对弦围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为，半径为3米的弧田，如图2所示．按照上述经验公式计算所得弧田面积大约是________平方米．(结果保留整数，≈1.73)‎ 答案　5‎ 解析　如题图2，由题意可得∠AOB＝，OA＝3，所以在Rt△AOD中，∠AOD＝，∠DAO＝，OD＝AO＝×3＝，可得CD＝3－＝，由AD＝AO·sin＝3×＝，可得AB＝2AD＝＝3.‎ 所以弧田面积S＝(弦×矢＋矢2)‎ ‎＝×＝＋≈5(平方米)．‎ ‎16.如图，在平面直角坐标系xOy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于B点，始边不动，终边运动．‎ ‎(1)若点B的横坐标为－，求tanα的值；‎ ‎(2)若△AOB为等边三角形，写出与角α终边相同的角β的集合；‎ ‎(3)若α∈，请写出弓形AB的面积S与α的函数关系式．‎ 解　(1)根据题意可得B，∴tanα＝±.‎ ‎(2)若△AOB为等边三角形，‎ 则B或B，‎ 当B时，α＝；‎ 当B时，α＝－.‎ ‎∴与角α终边相同的角β的集合是.‎ ‎(3)若α∈，‎ 则S扇形＝αr2＝α，‎ 而S△AOB＝×1×1×sinα＝sinα，‎ 故弓形AB的面积S＝α－sinα，α∈.‎