- 2021-07-01 发布 |
- 37.5 KB |
- 3页


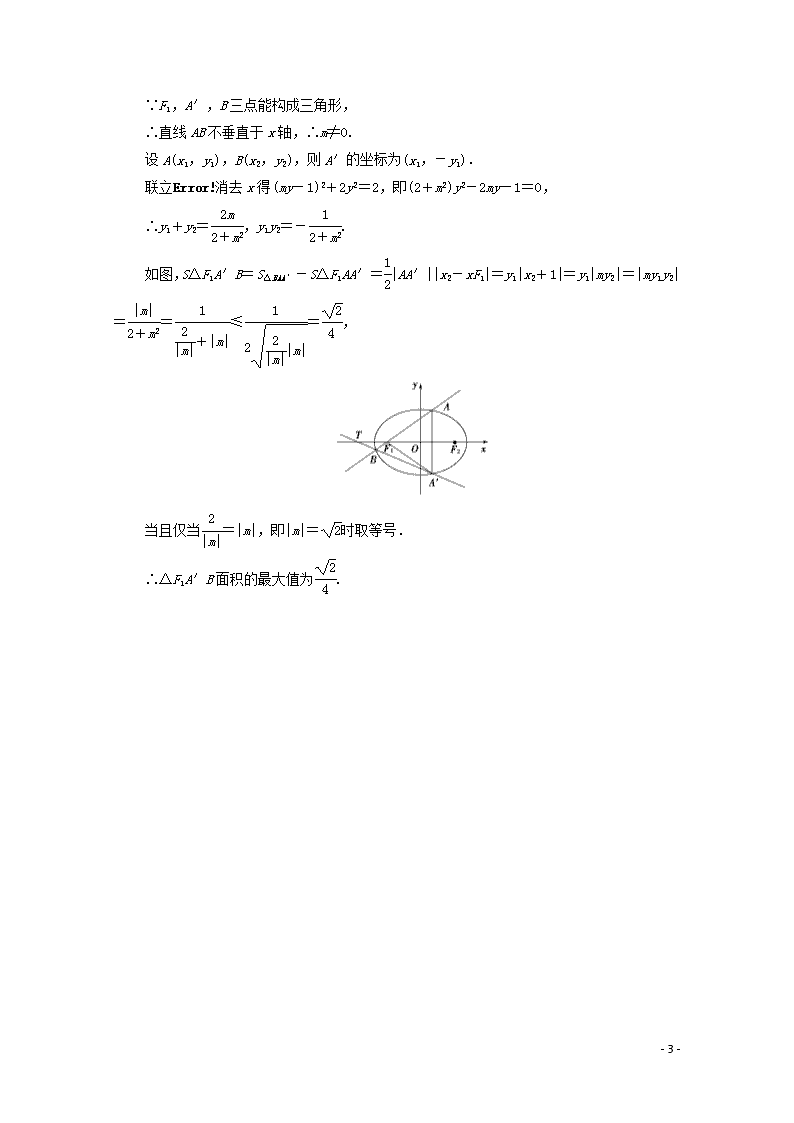
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021高考数学一轮复习课后限时集训55圆锥曲线中的范围最值问题文北师大版2
课后限时集训55 圆锥曲线中的范围、最值问题 建议用时:45分钟 1.(2019·开封模拟)已知椭圆+=1(a>b>0)上的点到右焦点F(c,0)的最大距离是+1,且1,a,4c成等比数列. (1)求椭圆的方程; (2)过点F且与x轴不垂直的直线l与椭圆交于A,B两点,线段AB的垂直平分线交x轴于点M(m,0),求实数m的取值范围. [解](1)由已知可得解得 所以椭圆的方程为+y2=1. (2)由题意得F(1,0),设直线AB的方程为y=k(x-1). 与椭圆方程联立得消去y可得(1+2k2)x2-4k2x+2k2-2=0. 设A(x1,y1),B(x2,y2),则x1+x2=,y1+y2=k(x1+x2)-2k=. 可得线段AB的中点为N. 当k=0时,直线MN为y轴,此时m=0. 当k≠0时,直线MN的方程为 y+=-, 化简得ky+x-=0.令y=0,得m=. 所以m==∈. 综上所述,m的取值范围为. 2.已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点. (1)若=2,求直线AB的斜率; (2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值. [解](1)依题意知F(1,0),设直线AB的方程为x=my+1. 将直线AB的方程与抛物线的方程联立,消去x得y2-4my-4=0. 设A(x1,y1),B(x2,y2), - 3 - 所以y1+y2=4m,y1y2=-4. ① 因为=2,所以y1=-2y2. ② 联立①和②,消去y1,y2,得m=±. 所以直线AB的斜率是±2. (2)由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于2S△AOB. 因为2S△AOB=2··|OF|·|y1-y2| = =4, 所以当m=0时,四边形OACB的面积最小,最小值是4. 3.已知椭圆C:+=1(a>b>0)的离心率为,左焦点为F1,点 A是椭圆C上位于x轴上方的一个动点,当直 线AF1的斜率为1时,|AF1|=. (1)求椭圆C的方程; (2)若直线AF1与椭圆C的另外一个交点为B,点A关于x轴的对称点为A′,求△F1A′B面积的最大值. [解](1)∵e==,∴a2=2c2. 又a2=b2+c2,∴b=c. ∴当直线AF1的斜率为1时,直线AF1通过椭圆的上顶点, ∴a=|AF1|=. 又a2=2c2,b=c,∴b=1, 椭圆C的方程为+y2=1. (2)∵A在x轴上方,∴直线AB的斜率不为0. 设直线AB的方程为x=my-1. ∵F1,A′,B三点能构成三角形, ∴直线AB不垂直于x轴,∴m≠0. - 3 - 设A(x1,y1),B(x2,y2),则A′的坐标为(x1,-y1). 联立消去x得(my-1)2+2y2=2,即(2+m2)y2-2my-1=0, ∴y1+y2=,y1y2=-. 如图,S△F1A′B=S△BAA′-S△F1AA′=|AA′||x2-xF1|=y1|x2+1|=y1|my2|=|my1y2|==≤=, 当且仅当=|m|,即|m|=时取等号. ∴△F1A′B面积的最大值为. - 3 -查看更多