【数学】2019届一轮复习苏教版矩阵乘法的概念学案

【数学】2019届一轮复习苏教版矩阵乘法的概念学案

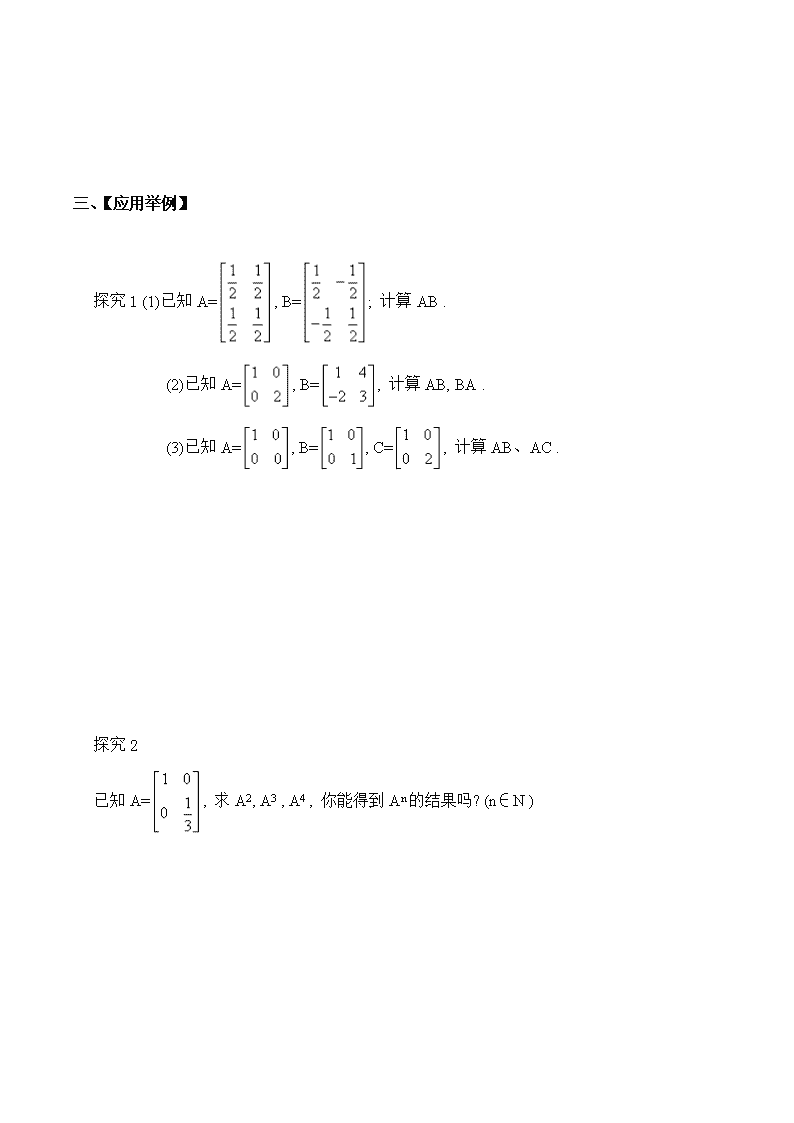
‎ 矩阵乘法的概念 ‎【考纲下载】1.掌握二阶矩阵乘法法则及矩阵乘法的几何意义.‎ ‎ 2.能灵活运用矩阵乘法进行平面图形的变换 .‎ ‎ 3.了解初等变换及初等变换矩阵的含义.‎ 一、【知识回顾】‎ 问题1.对向量先做变换矩阵为N=的反射变换T1, 得到向量, 再对所得向量做变换矩阵为M=的伸压变换T2得到向量, 这两次变换能否用一个矩阵来表示?‎ 问题2.矩阵乘法的乘法规则]‎ 问题3.矩阵乘法的几何意义 问题4.初等变换, 初等变换矩阵 二、【自学检测】‎ 计算:‎ ‎ (1) (2) ‎ ‎ (3) (4) ‎ 三、【应用举例】‎ 探究1 (1)已知A=, B=; 计算AB .‎ ‎ (2)已知A=, B= , 计算AB, BA .‎ ‎ (3)已知A=, B=, C=, 计算AB、AC .‎ 探究2 ]‎ 已知A=, 求A2, A3 , A4 , 你能得到An的结果吗? (n∈N )‎ ‎ ‎ ‎ 学, , ]‎ 探究3、已知梯形ABCD, 其中A(0 , 0) , B(3 , 0) , C(1 , 2) , D((1 , 2), 先将梯形作关于x轴的反射变换, 再将所得图形绕原点逆时针旋转90°.‎ ‎(1)求连续两次变换所对应的变换矩阵M ; ‎ ‎(2)求点A , B , C , D在TM作用下所得到的结果;‎ ‎(3)在平面直角坐标系内画出两次变换对应的几何图形, 并验证(2)中的结论.‎ 探究4、已知A= , B= , 求AB, 并对其几何意义给予 ‎ ]‎ 探究5.曲线在矩阵作用下变换得到什么图形？‎ 复习检测 ‎1.已知A= , 求A2 , A3 , 你能得到An的结果吗? (n∈N ) .‎ ‎2.计算, 并用文字描述二阶矩阵对应的变换方式.‎ ‎3.已知△ABC, 其中A(1 , 2), B(2 , 0), C(4 , -2), 先将三角形绕原点按顺时针旋转90°, 再将所得图形的横坐标伸长为原来的3倍, 纵坐标不变.‎ ‎ (1)求连续两次变换所对应的变换矩阵M ; ‎ ‎ (2)求点A , B , C在变换矩阵M作用下所得到的结果; ‎ ‎ (3)如果先将图形的横坐标伸长为原来的3倍, 再将所得图形绕原点顺时针旋转90°, 则连续两次变换所对应的变换矩阵M′是什么呢?‎ ‎4.设m , n∈k , 若矩阵A=把直线l : x－5y+1=0变换成另一直线 l′: 2x+y+3=0, 试求出m , n的值.‎