2019届二轮复习（理）2-5-2点、直线、平面之间的位置关系作业（全国通用）

2019届二轮复习（理）2-5-2点、直线、平面之间的位置关系作业（全国通用）

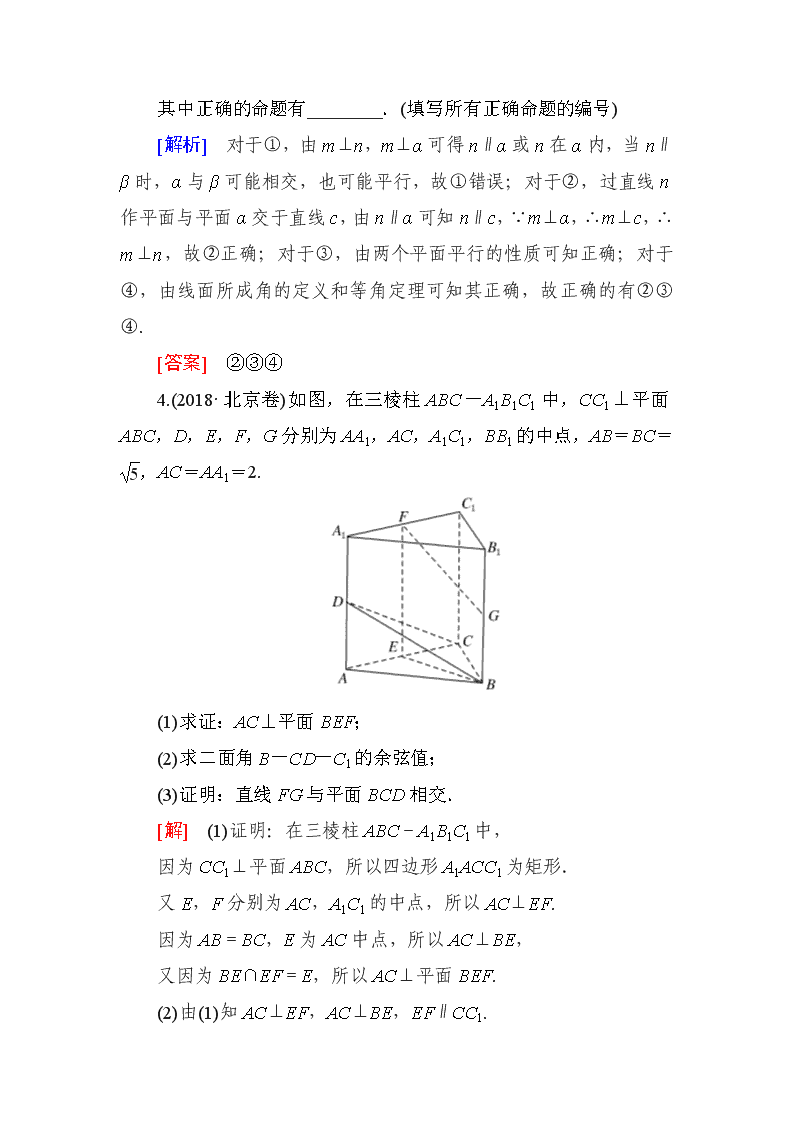
‎1．(2018·浙江卷)已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎[解析]　∵m⊄α，n⊂α，m∥n，∴m∥α，故充分性成立．而由m∥α，n⊂α，得m∥n或m与n异面，故必要性不成立．故选A.‎ ‎[答案]　A ‎2．(2017·全国卷Ⅱ)已知直三棱柱ABC－A1B1C1中，∠ABC＝120°，AB＝2，BC＝CC1＝1，则异面直线AB1与BC1所成角的余弦值为(　　)‎ A. B. C. D. ‎[解析]　解法一：将直三棱柱ABC－A1B1C1补形成直四棱柱ABCD－A1B1C1D1(如图)，连接AD1，B1D1，则AD1∥BC1.则∠B1AD1(或其补角)为异面直线AB1与BC1所成的角，易求得AB1＝，BC1＝AD1＝，B1D1＝.由余弦定理得cos∠B1AD1＝.故选C.‎ 解法二：以B为坐标原点，，的方向分别为y，z 轴的正方向，建立如图所示的空间直角坐标系，则B(0,0,0)．‎ ‎∵∠ABC＝120°，BC＝1，AB＝2，BB1＝1，‎ ‎∴A(0,2,0)，B1(0,0,1)，C1.‎ ‎∴＝(0，－2,1)，＝.‎ 设异面直线AB1与BC1所成的角为θ，‎ 则cosθ＝＝＝＝，故选C.‎ ‎[答案]　C ‎3．(2017·全国卷Ⅱ)α，β是两个平面，m，n是两条直线，有下列四个命题：‎ ‎①如果m⊥n，m⊥α，n∥β，那么α⊥β.‎ ‎②如果m⊥α，n∥α，那么m⊥n.‎ ‎③如果α∥β，m⊂α，那么m∥β.‎ ‎④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．‎ 其中正确的命题有________．(填写所有正确命题的编号)‎ ‎[解析]　对于①，由m⊥n，m⊥α可得n∥α或n在α内，当n∥‎ β时，α与β可能相交，也可能平行，故①错误；对于②，过直线n作平面与平面α交于直线c，由n∥α可知n∥c，∵m⊥α，∴m⊥c，∴m⊥n，故②正确；对于③，由两个平面平行的性质可知正确；对于④，由线面所成角的定义和等角定理可知其正确，故正确的有②③④.‎ ‎[答案]　②③④‎ ‎4.(2018·北京卷)如图，在三棱柱ABC－A1B1C1中，CC1⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB＝BC＝，AC＝AA1＝2.‎ ‎(1)求证：AC⊥平面BEF；‎ ‎(2)求二面角B－CD－C1的余弦值；‎ ‎(3)证明：直线FG与平面BCD相交．‎ ‎[解]　(1)证明：在三棱柱ABC－A1B1C1中，‎ 因为CC1⊥平面ABC，所以四边形A1ACC1为矩形．‎ 又E，F分别为AC，A1C1的中点，所以AC⊥EF.‎ 因为AB＝BC，E为AC中点，所以AC⊥BE，‎ 又因为BE∩EF＝E，所以AC⊥平面BEF.‎ ‎(2)由(1)知AC⊥EF，AC⊥BE，EF∥CC1.‎ 又CC1⊥平面ABC，所以EF⊥平面ABC.‎ 因为BE⊂平面ABC，所以EF⊥BE.‎ 如图建立空间直角坐标系E－xyz.‎ 由题意得B(0,2,0)，C(－1,0,0)，D(1,0,1)，F(0,0,2)，G(0,2,1)．‎ 所以＝(－1，－2,0)，＝(1，－2,1)．‎ 设平面BCD的法向量为n＝(x0，y0，z0)，‎ 则即 令y0＝－1，则x0＝2，z0＝－4.于是n＝(2，－1，－4)．‎ 又因为平面CC1D的一个法向量为＝(0,2,0)，‎ 所以cos〈n，〉＝＝－.‎ 由题知二面角B－CD－C1为钝角，所以其余弦值为－.‎ ‎(3)证明：由(2)知平面BCD的一个法向量为n＝(2，－1，－4)，＝(0,2，－1)．‎ 因为n·＝2×0＋(－1)×2＋(－4)×(－1)＝2≠0，所以直线FG与平面BCD相交．‎ ‎1.高考对此部分的命题较为稳定，一般为“一小一大”或“一大”，即一道选择或填空题和一道解答题或一道解答题．‎ ‎2．选择题一般在第3～5题的位置，填空题一般在第14题的位置，多考查线面位置关系的判断，难度较小．‎ ‎3．解答题多出现在第18或19题的位置，考查空间中平行或垂直关系的证明、利用空间向量求异面直线所成的角、线面角或二面角，难度中等．‎