房山区2020届高三一模 数学

房山区2020届高三一模 数学

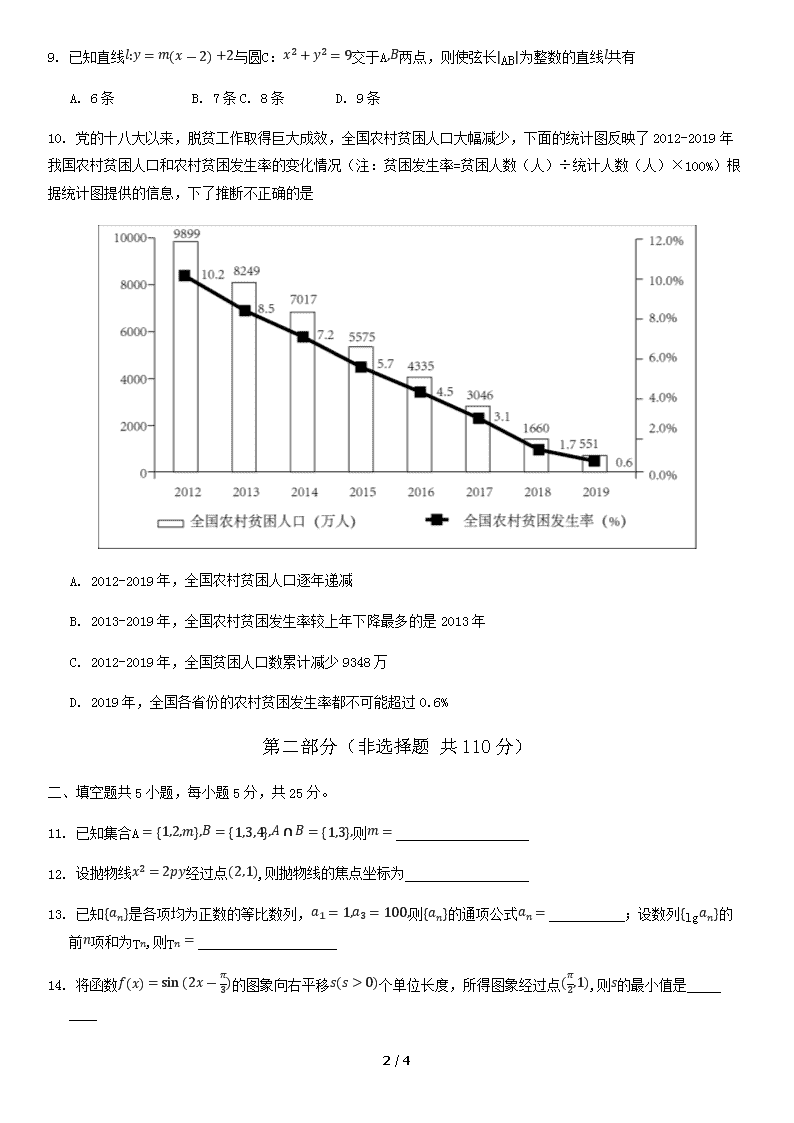
房山区2020届高三一模 数学试题 本试卷共6页，150分。考试时长120分钟。考生务必将答案答在答题卡上，在试卷上作答无效。考试结束后，将答题卡交回，试卷自行保存。‎ 第一部分（选择题 共40分）‎ 一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎1. 复数i‎3+i=‎ A. ‎1+3i B. ‎-1+3iC. ‎1-3i D. ‎‎-1-3i ‎2. 函数fx=tan⁡(x+π‎6‎)‎的最小正周期为 A. π‎3‎ B. π‎2‎ C. π D. ‎‎2π ‎3. 已知向量a=‎1,-‎‎1‎‎2‎,b=‎-2,m,‎若a与b共线，则b‎=‎ A. ‎3‎ B. ‎5‎C. ‎6‎ D. ‎‎2‎‎2‎ ‎4. 在二项式‎(1-2x)‎‎5‎的展开式中，x‎3‎的系数为 A. ‎40‎ B. ‎-40‎ C. ‎80‎ D. ‎‎-80‎ ‎5. 下列函数中，既是偶函数又在‎(0,+∞)‎上单调递减的是 A. y=‎x‎-2‎ B. y=‎lnx C. y=‎‎2‎‎-x D. ‎y=xsinx ‎6. 某三棱锥的三视图如右图所示，则该三棱锥的体积为 A. ‎4‎‎3‎ B. ‎8‎‎3‎C. ‎4‎ D. ‎‎8‎ ‎7. 已知函数fx=‎ax‎, x>-1‎bx+1,x≤-1‎若f‎-2‎=0,‎且fx在R上单调递增，则a的取值范围是 A. ‎(0,2]‎ B. ‎(1,2]‎C. ‎(1,+∞)‎ D. ‎‎[2,+∞)‎ ‎8. 设an是公差为d的等差数列，Sn为其前n项和，则“d<0‎”是“‎∀n∈N‎*‎,Sn+1‎<‎Sn”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 4 / 4‎ ‎9. 已知直线l:y=mx-2‎+2‎与圆C：x‎2‎+y‎2‎=9‎交于A,B两点，则使弦长AB为整数的直线l共有 A. 6条 B. 7条 C. 8条 D. 9条 ‎10. 党的十八大以来，脱贫工作取得巨大成效，全国农村贫困人口大幅减少，下面的统计图反映了2012-2019年我国农村贫困人口和农村贫困发生率的变化情况（注：贫困发生率=贫困人数（人）÷统计人数（人）×100%）根据统计图提供的信息，下了推断不正确的是 A. 2012-2019年，全国农村贫困人口逐年递减 B. 2013-2019年，全国农村贫困发生率较上年下降最多的是2013年 C. 2012-2019年，全国贫困人口数累计减少9348万 D. 2019年，全国各省份的农村贫困发生率都不可能超过0.6%‎ 第二部分（非选择题 共110分）‎ 二、填空题共5小题，每小题5分，共25分。‎ ‎11. 已知集合A=‎1,2,m,B=‎1,3,4‎,A∩B=‎1,3‎,‎则m=‎ ‎ ‎12. 设抛物线x‎2‎‎=2py经过点‎(2,1)‎,则抛物线的焦点坐标为 ‎ ‎13. 已知an是各项均为正数的等比数列，a‎1‎‎=1,a‎3‎=100,‎则an的通项公式an‎=‎ ；设数列lgan的前n项和为Tn,则Tn‎=‎ ‎ ‎14. 将函数fx=sin⁡(2x-π‎3‎)‎的图象向右平移s(s>0)‎个单位长度，所得图象经过点‎(π‎2‎,1)‎,则s的最小值是 ‎ 4 / 4‎ ‎15.如果方程x‎2‎‎4‎‎+yy=1‎所对应的曲线与函数y=f(x)‎的图象完全重合，那么对于函数y=f(x)‎有如下结论：‎ ‎①函数f(x)‎在R上单调递减；②y=f(x)‎的图象上的点到坐标原点距离的最小值为1；‎ ‎③函数f(x)‎的值域为‎-∞,2‎‎;‎④函数Fx=fx+x有且只有一个零点。‎ 其中正确结论的序号是 ‎ 注：本题给出的结论中，有多个符合题目要求。全部选对得5分，不选或有错选得0分，其他得3分。‎ 三、解答题共6题，共85分。解答应写出文字说明，盐酸步骤或证明过程。‎ ‎16.（本小题14分）在‎∆ABC中，a=‎2‎,c=‎10‎,‎ （补充条件）‎ ‎（I）求‎∆ABC的面积；（II）求sin⁡(A+B)‎从①b=4,‎②cosB=-‎5‎‎5‎,‎③sinA=‎‎10‎‎10‎这三个条件中任选一个，补充在上面问题中并作答。‎ 注：如果选择多个条件分别解答，按第一个解答计分。‎ ‎17.（本小题14分）随着移动互联网的发展，越来越多的人习惯用手机应用程序（简称app）获取新闻资讯，为了解用户对某款新闻类app的满意度，随机调查了300名用户，调研结果如下表：（单位：人）‎ 青年人 中年人 老年人 满意 ‎60‎ ‎70‎ x 一般 ‎55‎ ‎25‎ y 不满意 ‎25‎ ‎5‎ ‎10‎ ‎（I）从所有参与调研的人中随机选取1人，估计此人“不满意”的概率；‎ ‎（II）从参与调研的青年人和中年人中各随机选取1人，估计恰有1人“满意”的概率；‎ ‎（III）现需从参与调研的老年人中选择6人作进一步访谈，若在“满意”、“一般”、“不满意”的老年人中各取2人，这种抽样是否合理？说明理由 ‎18. （本小题14分）如图，在四棱锥P-ABCD中，PB⊥‎平面ABCD，AB⊥BC,AD∥BC,AD=2BC=2,AB=BC=PB,‎点E为棱PD的中点。‎ ‎（I）求证：CE∥‎平面PAB;‎（II）求证：AD⊥‎平面PAB;‎（III）求二面角E-AC-D的余弦值.‎ 4 / 4‎ ‎19. （本小题14分）已知椭圆C:x‎2‎a‎2‎+y‎2‎b‎2‎=1(a>b>0)‎过A‎2,0‎,B(0,1)‎两点.‎ ‎（I）求椭圆C的方程和离心率的大小；‎ ‎（II）设M，N是y轴上不同的两点，若两点的纵坐标互为倒数，直线AM与椭圆C的另一个交点为P，直线AN与椭圆C的另一个交点为Q，判断直线PQ与x轴的位置关系，并证明你的结论。‎ ‎20. （本小题15分）已知函数fx=2x‎3‎-ax‎2‎+2‎ ‎（I）求曲线y=f(x)‎在点‎(0,f(0))‎处的切线方程；（II）讨论函数f(x)‎的单调性；‎ ‎（III）若a>0‎,设函数gx=fx,g(x)‎在‎[-1,1]‎上的最大值不小于3，求a的取值范围.‎ ‎21.（本小题14分）在一个有穷数列的每相邻两项之间插入这两项的和，形成新的数列，我们把这样的操作称为该数列的一次“Z拓展”，如数列‎1，2‎第1次“Z拓展”后得到数列‎1，3，2，‎第‎2‎次“Z拓展”后得到数列‎1，4，3，5，2‎.设数列a,b,c经过第n次“Z拓展”后所得数列的项数记为Pn,所有项的和记为Sn ‎（I）求P‎1‎‎,P‎2‎;‎（II）若Pn‎≥2020,‎求n的最小值；‎ ‎（III）是否存在实数a,b,c,‎使得数列Sn为等比数列？若存在，求a,b,c满足的条件；若不存在，说明理由 4 / 4‎