高一数学复习必修

高一数学复习必修

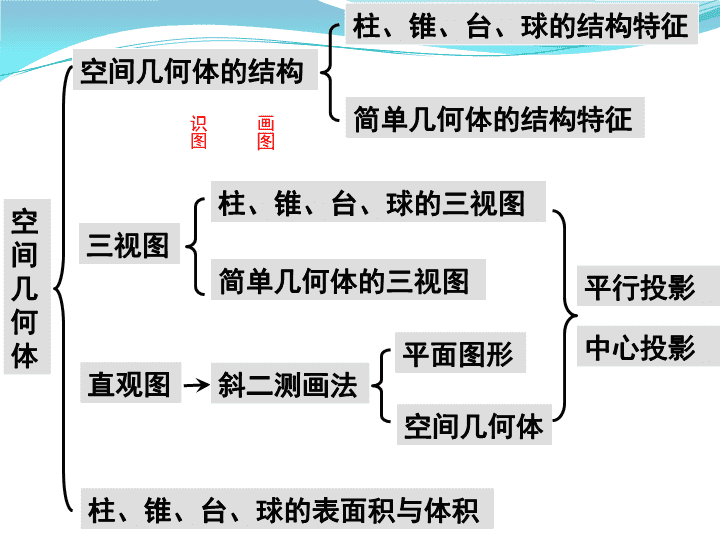
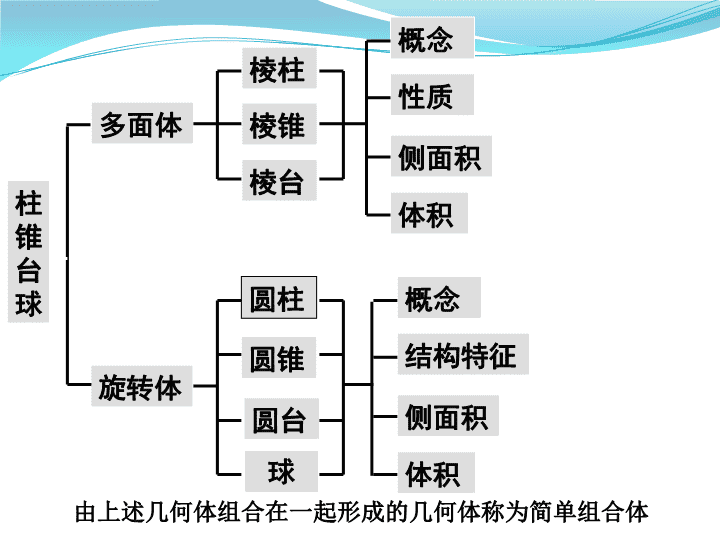
人教版A必修 2 高一数学复习课件 ( 必修 2 ） 空间几何体 空间几何体的结构 柱、锥、台、球的结构特征 简单几何体的结构特征 三视图 柱、锥、台、球的三视图 简单几何体的三视图 直观图 斜二测画法 平面图形 空间几何体 中心投影 柱、锥、台、球的表面积与体积 平行投影 画 图 识图 柱锥台球 圆锥 圆台 多面体 旋转体 圆柱 棱柱 棱锥 棱台 概念 结构特征 侧面积 体积 球 概念 性质 侧面积 体积 由上述几何体组合在一起形成的几何体称为简单组合体 柱、锥、台、球的结构特征 D A B C E F F’ A’ E’ D’ B’ C’ 棱柱 结构特征 有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面围成的多面体。 侧棱 侧面 底面 顶点 注意： 有两个面互相平行，其余各面都是平行四边形的几何体一定是棱柱吗？ 答：不一定是．如图所示，不是棱柱． 棱柱的性质 1. 侧棱都相等，侧面都是平行四边形； 2. 两个底面与平行于底面的截面都是全等的多边形； 3. 平行于侧棱的截面都是平行四边形； 1 、 按侧棱是否和底面垂直分类 ： 棱柱 斜棱柱 直棱柱 正棱柱 其它直棱柱 2 、 按底面多边形边数分类 ： 棱柱的分类 三棱柱、四棱柱、 五棱柱、 ······ 棱柱的分类 按边数分 按侧棱是否与底面垂直分 斜棱柱 直棱柱 正棱柱 三棱柱 四棱柱 五棱柱 四棱柱 平行六面体 长方体 直平行六面体 正四棱柱 正方体 底面变为 平行四边形 侧棱与底面 垂直 底面是 矩形 底面为 正方形 侧棱与底面 边长相等 几种六面体的关系： 柱、锥、台、球的结构特征 棱锥 S A B C D 顶点 侧面 侧棱 底面 结构特征 有一个面是多边形，其余各面都是有一个公共顶点的三角形。 按底面多边形的边数，可以分为三棱锥、四棱锥、五棱锥、 …… A B C D S 棱锥的分类 正棱锥：底面是正多边形，并且顶点在底面内的射影是底面中心的棱锥。 【 知识梳理 】 棱锥 1 、 定义： 有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫棱锥。 如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面中心，这样的棱锥叫做正棱锥。 2 、 性质 Ⅰ 、正棱锥的性质 (1) 各侧棱相等，各侧面都是全等的等腰三角形。 (2) 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形；棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。 正棱锥性质 2 棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形 Rt⊿ SOH Rt⊿ SOB Rt⊿ SHB Rt⊿ BHO 棱台由棱锥截得而成，所以在棱台中也有类似的直角梯形。 柱、锥、台、球的结构特征 棱台 结构特征 A B C D A’ B’ C’ D’ 用一个平行于棱锥底面的平面去截棱锥 , 底面与截面之间的部分是棱台 . B’ 柱、锥、台、球的结构特征 圆柱 A A’ O B O’ 轴 底面 侧面 母线 结构特征 以矩形的一边所在直线为旋转轴 , 其余三边旋转形成的曲面所围成的几何体叫做圆柱。 B’ 柱、锥、台、球的结构特征 圆锥 S 顶点 A B O 底面 轴 侧面 母线 结构特征 以直角三角形的一条直角边所在直线为旋转轴 , 其余两边旋转形成的曲面所围成的几何体叫做圆锥。 柱、锥、台、球的结构特征 圆台 结构特征 O O’ 用一个平行于圆锥底面的平面去截圆锥 , 底面与截面之间的部分是圆台 . 柱、锥、台、球的结构特征 球 结构特征 O 半径 球心 以半圆的直径所在直线为旋转轴 , 半圆面旋转一周形成的旋转体 . 空间几何体的表面积和体积 圆柱的侧面积： 圆锥的侧面积： 圆台的侧面积： 球的表面积： 柱体的体积： 锥体的体积： 台体的体积： 球的体积： 面积 体积 练习 C 1. 设棱锥的底面面积为 8cm 2 ，那么这个棱锥的中截面 ( 过棱锥的中点且平行于底面的截面 ) 的面积是 ( ) (A)4cm 2 (B) cm 2 (C)2cm 2 (D) cm 2 2. 若一个锥体被平行于底面的平面所截，若截面面积是底面面积的四分之一，则锥体被截面截得的一个小锥与原棱锥体积之比为 ( ) (A)1 : 4 (B) 1 : 3 (C) 1 : 8 (D) 1 : 7 C   练 4 ：一个正三棱锥的底面边长是 6 ，高是 ，那么这个正三棱 锥的体积是（ ） （ A ） 9 （ B ） （ C ） 7 （ D ） 练 5 ：一个正三棱台的上、下底 面边长分别为 3cm 和 6cm ， 高是 1.5cm ，求三棱台的侧 面积。 A 6. 如图，等边圆柱（轴截面为正方形 ABCD ） 一只蚂蚁在 A 处，想吃 C 1 处的蜜糖，怎么走才最快，并求最短路线的长？ A B C D A D C B 二、空间几何体的三视图和直观图 中心投影 平行投影 斜二测画法 俯视图 侧视图 正视图 三视图 直观图 投影 知识框架 A B C a b c A B C a b c H H 平行投影法   平行投影法 投影线相互平行的投影法 . （ 1 ）斜投影法 投影线倾斜于投影面的平行投影法称为斜投影法 . （ 2 ）正投影法 投影线垂直于投影面的平行投影法称为正投影法 . 斜投影法   正投影法 正 投 影 三视图的形成原理 有关概念 物体向投影面投 影 所得到的图形称为 视图 。 如果物体向三个互相垂直的投影面分别投影，所得到的三个图形摊平在一个平面上，则就是 三视图 。 三视图的形成 正视图 俯视图 侧视图 俯视图 侧视图 正视图 展开图 长对正 , 高平齐 , 宽相等 . 长 长 高 高 宽 宽 三视图的作图步骤 正视图方向 1. 确定视图方向 侧视图方向 俯视图方向 2. 先画出能反映物体真实形状的一个视图 4. 运用长对正、高平齐、宽相等的原则画出其它视图 5. 检查 , 加深 , 加粗。 (1) 一般几何体， 投影各顶点 , 连接。 (2) 常见几何体 , 熟悉。 总结 画三视图 ： 两个三角形， 一般为锥体 两个矩形， 一般为柱体 两个梯形， 一般为台体 两个圆， 一般为球 三视图中， 斜二测画法步骤是： （ 1 ）在已知图形中取互相垂直的 x 轴和 y 轴，两轴相交于点 O 。画直观图时，把它们画成对应的 x’ 轴和 y’ 轴，两轴交于点 O’ ，且使 ∠ x’O’y’=45° （或 135 ° ），它们确定的平面表示水平面。 （ 2 ）已知图形中平行于 x 轴或 y 轴的线段，在直观图中分别画成平行于 x’ 轴或 y’ 轴的线段。 （ 3 ）已知图形中平行于 x 轴的线段，在直观图中保持原长度不变，平行于 y 轴的线段，长度为原来的一半。 练 1 ：圆柱的正视图、侧视图都是 ，俯视图是 ； 圆锥的正视图、侧视图都是 ，俯视图是 ； 圆台的正视图、侧视图都是 ，俯视图是 。 练 2 ：利用斜二测画法可以得到： ①三角形的直观图是三角形；②平行四边形的直观图是平 行四边形；③正方形的直观图是正方形；④菱形的直观图 是菱形。以上结论正确的是（ ） （ A ）①② （ B ）① （ C ）③④ （ D ）①②③④ 矩形 圆 三角形 圆及圆心 梯形 圆环 A 练 3 ：根据三视图可以描述物体的形状，其中根据左视图可以判 断物体的 ；根据俯视图可以判断物体的 ；根据正视图可以判断物体的 。 宽度和高度 长度和宽度 长度和高度 “ 正、侧一样高，正、俯一样长，俯、侧一样宽” . 练 4 ：某生画出了图中实物的正视图与俯视图，则下列判断正确的 是（ ） A. 正视图正确，俯视图正确 B. 正视图正确，俯视图错误 C. 正视图错误，俯视图正确 D. 正视图错误，俯视图错误 俯视 正视图 俯视图 左视 正视 练 5 ：下图中三视图所表示物体的形状为（ ） 主视图 左视图 俯视图 一个倒放着的圆锥 B 6. 一平面图形的直观图如图所示，它原来的面积是 （ ） 2 2 o’ A B x ’ y ’ A. 4 B. C. D. 8 A 7. 如图所示， △ ABC 的直观图△ A’B’C’, 这里△ A’B’ C’ 是边长为 2 的正三角形，作出△ ABC 的平面图 ，并求△ ABC 的面积 . O’ A’ B’ x ’ y ’ C’ 正三棱柱的侧棱为 2 ，底面是边长为 2 的正三角形，则侧视图的面积为（ ） B. C. D. A. B 侧视图 练习 8 ： 将正三棱柱截去三个角（如图 1 所示分别是三边的中点）得到几何体如图 2 ，则该几何体按图 2 所示方向的侧视图（或称左视图）为（ ） E B A ． B E B ． B E C ． B E D ． A E F D I A H G B C 侧视 图 1 图 2 E F D C A B P Q 9 ： (1) 如图是一个空间几何体的三视图，如果直角三角形的直角边长均为 1 ，那么几何体的体积为 ( ) A ． 1 B ． 　 C ． D ． C 正视图 侧视图 俯视图 1 1 1 练习 10 ： 20 20 主视图 20 侧视图 10 10 20 俯视图 11. 已知某个几何体的三视图如图 2 ，根据图中标出的尺寸 （单位： cm ），可得这个几何体的体积是 ________. 第二章 点、直线、平面之间的位置关系 四个公理 直线与直线位置关系 三类关系 直线与平面位置关系 平面与平面位置关系 线线角 三种角 线面角 二面角 线面平行的判定定理与性质定理 线面垂直的判定定理与性质定理 八个定理 面面平行的判定定理与性质定理 面面垂直的判定定理与性质定理 四个公理 公理 1 ：如果一条直线上有两点在一个平面内，那么直线在平面内 . （常用于证明直线在平面内） 公理 2 ：不共线的三点确定一个平面 . （用于确定平面） . 推论 1 ：直线与直线外的一点确定一个平面 . 推论 2 ：两条相交直线确定一个平面 . 推论 3 ：两条平行直线确定一个平面 . 公理 3 ：如果两个平面有一个公共点，那么它们还有公共点，这些公共点的集合是一条直线（两个平面的交线） . 平行公理 ：平行于同一条直线的两条直线互相平行 . 三类关系 1. 线线关系： 三类关系 2. 线面关系 直线与平面所成的角（简称线面角）：若直线与平面斜交， 则平面的斜线与该斜线在平面内射影的夹角。 3. 面面关系 八个定理 八个定理 八个定理 八个定理 八个定理 八个定理 八个定理 立体几何解题中的转化策略 大策略：空间 平面 位置关系的相互转化 小策略： ③ 平行关系 垂直关系 ① 平行转化：线线平行 线面平行 面面平行 ② 垂直转化：线线垂直 线面垂直 面面垂直 例 1 ：在棱长为 1 的正方体 ABCD — A 1 B 1 C 1 D 1 中， (1) 求异面直线 A 1 B 与 B 1 C 所成的角的大小 ; (2) 求直线 A 1 B 与平面 BB 1 D 1 D 所成的角 ; (4) 求证 : 平面 A 1 BD// 平面 CB 1 D 1 ; (7) 求点 A 1 到平面 CB 1 D 1 的距离 . (3) 求二面角 A—BD—A 1 的正切值 ; 经典例题 A B C D A 1 B 1 C 1 D 1 立体几何解题中的转化策略 例 2 ： 立体几何解题中的转化策略 平面中的数量关系隐藏着三角形特征！ 练习 1 ： 立体几何解题中的转化策略 转化需要辅助线的添加！ 练习 1 ： 策略：线面平行转化成线线平行（空间转化平面） 立体几何解题中的转化策略 一个多面体的直观图及三视图如图所示： 例 3 （综合题型）： （其中 分别是 、 的中点） 正视图 侧视图 俯视图 立体几何解题中的转化策略 一个多面体的直观图及三视图如图所示： 例 3 （综合题型）： （其中 分别是 、 的中点） 直三棱柱 （ 1 ）求该多面体的表面积与体积； 策略：空间几何体的相互转化 可考虑将该多面体补图成正方体 解： 立体几何解题中的转化策略 一个多面体的直观图及三视图如图所示： 例 3 （综合题型）： （其中 分别是 、 的中点） 直三棱柱 （ 2 ）求证： 平面 ； 策略：利用中位线将线面平行转化成线线平行 解： 立体几何解题中的转化策略 一个多面体的直观图及三视图如图所示： 例 3 （综合题型）： （其中 分别是 、 的中点） 直三棱柱 （ 3 ）求二面角 的正切值； 策略：将二面角转化成平面角 , 先找后求 解： 立体几何解题中的转化策略 一个多面体的直观图及三视图如图所示： 例 3 （综合题型）： （其中 分别是 、 的中点） 直三棱柱 （ 4 ）求多面体 的体积； 策略：将点面距离转化成点线距离 解： 必修二复习（解析几何） 解析几何知识网络图 直线和圆 直线的斜率与倾斜角 直线方程的五种形式 点到直线的距离公式 两条直线的位置关系 圆的标准及一般方程 直线与圆的位置关系 圆与圆的位置关系 空间两点的距离公式 了解空间直角坐标系 直线与直线方程 直线的倾斜角和斜率 直线的方程 两直线的位置关系 一、直线与直线方程 1 、直线的倾斜角 倾斜角的取值范围是 2 、直线的斜率 意义：斜率表示倾斜角不等于 90 0 的直线对于 x 轴的倾斜程度。 直线的斜率计算公式 ： 形式 条件 方程 应用范围 点斜式 过点 ( x 0 , y 0 ), 斜率为 k 斜截式 在 y 轴上的截距为 b , 斜率为 k 两点式 过 P 1 （ x 1 , y 1 ), P 2 （ x 2 , y 2 ) 截距式 在 y 轴上的截距为 b , 在 x 轴上的截距为 a 一般式 任何直线 两直线平行的判定 : 方法： 2) 若 1) 若 两直线相交的判定 : 方法： 1) 若 相交 2) 若 相交 两直线垂直的判定 : 方法： 2) 若 1) 若 （ 1 ）点 到直线 距离： 4. 点到直线的距离，平行线的距离 （ 2 ）直线 到直线 的距离： 对称问题 1) 中心对称 ( 点关于点的对称点 , 直线关于点的对称直线 ) 解决方法 中点坐标公式 3) 轴对称 ( 点关于直线的对称点 , 直线关于直线的对称直线 ) 解决方法 (1) 垂直 (2) 中点在对称轴上 题型一 求直线的方程 例 1 、求适合下列条件的直线方程： （ 1 ）经过点 P （ 3 ， 2 ），且在两坐标轴上的截距 相等； （ 2 ）经过点 A （ -1 ， -3 ），且倾斜角等于直线 y = 3 x 的倾斜角的 2 倍 . 选择适当的直线方程形式，把所需要 的条件求出即可 . 解 （ 1 ） 方法一 设直线 l 在 x , y 轴上的截距均为 a , 若 a =0 ，即 l 过点（ 0 ， 0 ）和（ 3 ， 2 ）， ∴ l 的方程为 y = x ，即 2 x -3 y =0. 思维启迪 若 a ≠0 ，则设 l 的方程为 ∵ l 过点（ 3 ， 2 ），∴ ∴ a =5 ，∴ l 的方程为 x + y -5=0, 综上可知，直线 l 的方程为 2 x -3 y =0 或 x + y -5=0. 方法二 由题意知，所求直线的斜率 k 存在且 k ≠0, 设直线方程为 y -2= k ( x -3), 令 y =0 ，得 x =3- , 令 x =0, 得 y =2-3 k , 由已知 3- =2-3 k ，解得 k =-1 或 k = , ∴ 直线 l 的方程为 y -2=- （ x -3 ）或 y -2= ( x -3), 即 x + y -5=0 或 2 x -3 y =0. （ 2 ）由已知：设直线 y =3 x 的倾斜角为 ， 则所求直线的倾斜角为 2 . ∵tan =3,∴tan 2 = 又直线经过点 A （ -1 ， -3 ）， 因此所求直线方程为 y +3=- ( x +1), 即 3 x +4 y +15=0. 题型二 直线的斜率 【 例 2 】 已知直线 l 过点 P （ -1 ， 2 ），且与以 A （ -2 ， -3 ）， B （ 3 ， 0 ）为端点的线段相交， 求直线 l 的斜率的取值范围 . 分别求出 PA 、 PB 的斜率，直线 l 处 于直线 PA 、 PB 之间，根据斜率的几何意义利 用数形结合即可求 . 解 方法一 如图所示，直线 PA 的 斜率 直线 PB 的斜率 思维启迪 当直线 l 绕着点 P 由 PA 旋转到与 y 轴平行的位置 PC 时，它的斜率变化范围是［ 5 ， +∞ ）； 当直线 l 绕着点 P 由 PC 旋转到 PB 的位置时，它的斜 率的变化范围是 ∴直线 l 的斜率的取值范围是 方法二 设直线 l 的斜率为 k ，则直线 l 的方程为 y -2= k （ x +1 ）， 即 kx - y + k +2=0. ∵ A 、 B 两点在直线的两侧或其中一点在直线 l 上， ∴（ -2 k +3+ k +2 ）（ 3 k -0+ k +2 ）≤ 0 ， 即 （ k -5 ）（ 4 k +2 ）≥ 0 ，∴ k ≥5 或 k ≤- . 即直线 l 的斜率 k 的取值范围是 ∪［ 5 ， +∞ ） . 方法一 运用了数形结合思想 . 当直线 的倾斜角由锐角变到直角及由直角变到钝角时， 需根据正切函数 y =tan 的单调性求 k 的范围，数 形结合是解析几何中的重要方法 . 解题时，借助图 形及图形性质直观判断，明确解题思路，达到快 捷解题的目的 . 方法二则巧妙利用了不等式所表示 的平面区域的性质使问题得以解决 . 探究提高 题型三 两直线的位置关系 例 3 ： 已知直线方程为 (2 ＋ λ ) x ＋ (1 － 2 λ ) y ＋ 9 － 3 λ ＝ 0. (1) 求证不论 λ 取何实数值，此直线必过定点； (2) 过这定点引一直线，使它夹在两坐标轴 间的线段被这点 平分，求这条直线方程 . 即点 ( － 3 ，－ 3) 适合方程 2 x ＋ y ＋ 9 ＋ λ ( x － 2 y － 3) ＝ 0 ，也就 是适合方程 (2 ＋ λ ) x ＋ (1 － 2 λ ) y ＋ 9 － 3 λ ＝ 0. 解： 把直线方程整理为 2 x ＋ y ＋ 9 ＋ λ ( x － 2 y － 3) ＝ 0. 所以，不论 λ 取何实数值，直线 (2 ＋ λ ) x ＋ (1 － 2 λ ) y ＋ 9 － 3 λ ＝ 0 必过定点 ( － 3 ，－ 3) ． (2) 设经过点 ( － 3 ，－ 3) 的直线与两坐标轴分别交于 A ( a, 0) ， B (0 ， b ) ． 解得 a ＝－ 6 ， b ＝－ 6. 即 x ＋ y ＋ 6 ＝ 0. 练 1 、过 的直线 与线段 相交，若 ， 求 的斜率 的取值范围。 2 、证明： 三点共线。 3 、设直线 的斜率为 ，且 ，求直线的倾斜角 的取值范围。 4 、已知直线 的倾斜角的正弦值为 ，且它与两坐标轴围成 的三角形面积为 ，求直线 的方程。 答案： 1 、 ； 2 、方法：① ② ③ ； 3 、 ； 4 、 、 、 、 。 练 5 、 为何值时，直线 与 平行？垂直？ 练 6 、求过点 且与原点的距离为 的直线方程。 答案： 1 、判断 是否为 ， 时垂直； 2 、 ； 9 、 （ 1 ）求 A （ -2 ， 3 ）关于直线对称点 B 的坐标； （ 2 ）光线自 A （ -3 ， 3 ）射出，经 x 轴反射以后经过点 B （ 2 ， 5 ），求入射光线和反射光线的直线方程； （ 3 ）已知 M （ -3 ， 5 ）， N （ 2 ， 15 ），在直线上找一点 P ，使 |PM|+|PN| 最小，并求出最小值 D A ． ab ＞ 0 ， bc ＞ 0 C ． ab ＜ 0 ， bc ＞ 0 B ． ab ＞ 0 ， bc ＜ 0 D ． ab ＜ 0 ， bc ＜ 0 10 、若直线 ax ＋ by ＋ c ＝ 0 在第一、二、 三象限，则 ( ) 圆 的 方 程 直线与圆、圆与圆的位置关系 圆与圆方程 求曲线方程 圆的标准方程 圆的一般方程 圆的参数方程 二、圆的方程 （ 1 ）曲线上的点的坐标都是这个方程 的解； （ 2 ）以这个方程的解为坐标的点都是曲线上的点， 1. 曲线与方程 （ 1 ）建立适当的坐标系，用 (x ， y) 表示曲线上 任意 一点 M 的坐标； （ 2 ）用坐标 x,y 表示关系式，即列出方程 f(x,y)=0; （ 3 ）化简方程 f(x,y)= 0; （ 4 ）验证 x 、 y 的取值范围。 2. 求曲线方程 圆的标准方程 圆的一般方程 圆的参数方程 1.( 全国 ) 圆心为 (1,2) 且与直线 5x-12y-7=0 相切的圆的方程为 2. 圆心在直线 2x-y-7=0 上的圆 C 与 y 轴交于两点 A(0,-4),B(0,-2), 求圆 C 的方程 . 3. △ABC 的三个顶点的坐标分别是 A(5,1),B(7,-3),C(2,-8), 求它的外接圆的方程 . 位置关系 直线与圆的位置关系 : 或 或 或 相离 相切 相交 判断方法 d>R+r d=R+r d= |R-r| |R-r|R+r d=R+r R-r

查看更多