2018届二轮复习(理) 解析几何学案(全国通用)
回扣8 解析几何
1.直线方程的五种形式
(1)点斜式:y-y1=k(x-x1)(直线过点P1(x1,y1),且斜率为k,不包括y轴和平行于y轴的直线).
(2)斜截式:y=kx+b(b为直线l在y轴上的截距,且斜率为k,不包括y轴和平行于y轴的直线).
(3)两点式:=(直线过点P1(x1,y1),P2(x2,y2),且x1≠x2,y1≠y2,不包括坐标轴和平行于坐标轴的直线).
(4)截距式:+=1(a,b分别为直线的横、纵截距,且a≠0,b≠0,不包括坐标轴、平行于坐标轴和过原点的直线).
(5)一般式:Ax+By+C=0(其中A,B不同时为0).
2.直线的两种位置关系
当不重合的两条直线l1和l2的斜率存在时:
(1)两直线平行l1∥l2⇔k1=k2.
(2)两直线垂直l1⊥l2⇔k1·k2=-1.
提醒 当一条直线的斜率为0,另一条直线的斜率不存在时,两直线也垂直,此种情形易忽略.
3.三种距离公式
(1)A(x1,y1),B(x2,y2)两点间的距离|AB|=.
(2)点到直线的距离d=(其中点P(x0,y0),直线方程为Ax+By+C=0).
(3)两平行线间的距离d=(其中两平行线方程分别为l1:Ax+By+C1=0,l2:Ax+By+C2=0).
提醒 应用两平行线间距离公式时,注意两平行线方程中x,y的系数应对应相等.
4.圆的方程的两种形式
(1)圆的标准方程:(x-a)2+(y-b)2=r2.
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
5.直线与圆、圆与圆的位置关系
(1)直线与圆的位置关系:相交、相切、相离,代数判断法与几何判断法.
(2)圆与圆的位置关系:相交、内切、外切、外离、内含,代数判断法与几何判断法.
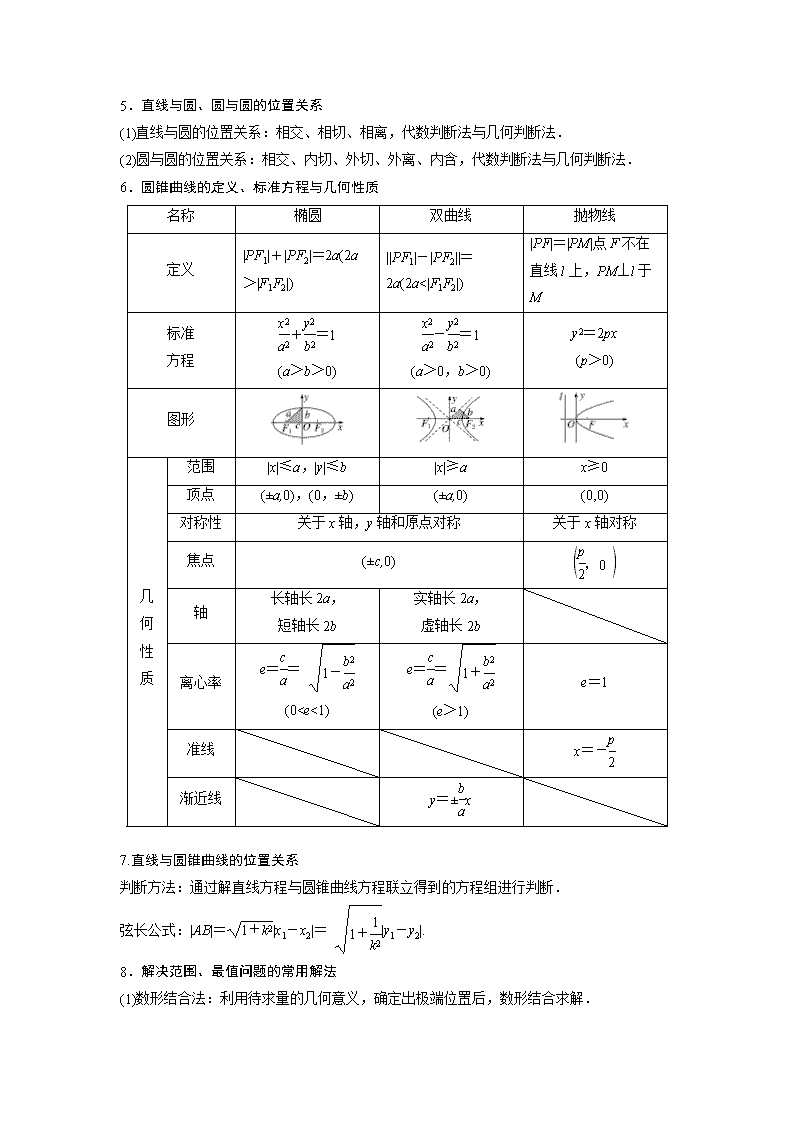
6.圆锥曲线的定义、标准方程与几何性质
名称
椭圆
双曲线
抛物线
定义
|PF1|+|PF2|=2a(2a>|F1F2|)
||PF1|-|PF2||=2a(2a<|F1F2|)
|PF|=|PM|点F不在直线l上,PM⊥l于M
标准
方程
+=1
(a>b>0)
-=1
(a>0,b>0)
y2=2px
(p>0)
图形
几
何
性
质
范围
|x|≤a,|y|≤b
|x|≥a
x≥0
顶点
(±a,0),(0,±b)
(±a,0)
(0,0)
对称性
关于x轴,y轴和原点对称
关于x轴对称
焦点
(±c,0)
轴
长轴长2a,
短轴长2b
实轴长2a,
虚轴长2b
离心率
e==
(0
0)相交于A,B两点,点F为抛物线的焦点,△ABF为直角三角形,则双曲线的离心率为( )
A.3 B.2 C. D.
答案 A
解析 依题意知,抛物线的准线为x=-2,代入双曲线方程得
y=±·,
不妨设A.
∵△FAB是等腰直角三角形,
∴=p=4,求得a=,
∴双曲线的离心率为e====3,
故选A.
8.若点O和点F分别为椭圆+=1的中心和左焦点,点P为椭圆上的任意一点,则·的最大值为( )
A.2 B.3
C.6 D.8
答案 C
解析 由题意得F(-1,0),设点P(x0,y0),
则y=3(-2≤x0≤2).
·=x0(x0+1)+y=x+x0+y
=x+x0+3
=(x0+2)2+2.
又因为-2≤x0≤2,所以当x0=2时,·取得最大值,最大值为6,故选C.
9.已知函数y=f(x)=ax+1-2(a>0且a≠1)的图象恒过定点A,设抛物线E:y2=4x上任意一点M到准线l的距离为d,则d+的最小值为( )
A.5 B.
C. D.
答案 C
解析 当x+1=0时,y=-1,故A(-1,-1),设抛物线焦点为F(1,0),根据抛物线的定义可知,d+的最小值为=.
10.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1,F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=30°时,这一对相关曲线中椭圆的离心率是( )
A.7-4 B.2-
C.-1 D.4-2
答案 B
解析 由题意设椭圆方程为+=1,
双曲线方程为-=1,且c=c1.
由题意·=1,(*)
由∠F1PF2=30°及余弦定理,得
椭圆中:4c2=4a2-(2+)|PF1||PF2|,
双曲线中:4c2=4a+(2-)|PF1||PF2|,
可得b=(7-4)b2,代入(*)式,
c4=aa2=(c2-b)a2=(8-4)c2a2-(7-4)a4,
即e4-(8-4)e2+(7-4)=0,
得e2=7-4,即e=2-,故选B.
11.已知直线l:mx-y=1,若直线l与直线x+m(m-1)y=2垂直,则m的值为________;动直线l:mx-y=1被圆C:x2-2x+y2-8=0截得的最短弦长为________.
答案 0或2 2
解析 由两直线垂直的充要条件得m×1+(-1)×m(m-1)=0,∴m=0或m=2;圆的半径为3,当圆心(1,0)到直线的距离最长,即d==时,弦长最短,此时弦长为2=2.
12.已知直线l:mx+y+3m-=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2,则|CD|=________.
答案 4
解析 设AB的中点为M,由题意知,圆的半径R=2,|AB|=2,所以|OM|=3,解得m=-,
由解得A(-3,),B(0,2),
则AC的直线方程为y-=-(x+3),BD的直线方程为y-2=-x,令y=0,解得C(-2,0),D(2,0),所以|CD|=4.
13.已知F1,F2是双曲线-=1的焦点,PQ是过焦点F1的弦, 且PQ的倾斜角为60°,那么|PF2|+|QF2|-|PQ|的值为________.
答案 16
解析 由双曲线方程-=1知,2a=8,
由双曲线的定义,得|PF2|-|PF1|=2a=8, ①
|QF2|-|QF1|=2a=8, ②
①+②得|PF2|+|QF2|-(|QF1|+|PF1|)=16.
∴|PF2|+|QF2|-|PQ|=16.
14.在直线y=-2上任取一点Q,过Q作抛物线x2=4y的切线,切点分别为A,B,则直线AB恒过定点________.
答案 (0,2)
解析 设Q(t,-2),A(x1,y1),B(x2,y2),抛物线方程变为y=x2,则y′=x,则在点A处的切线方程为y-y1=x1(x-x1),化简得y=x1x-y1,同理,在点B处的切线方程为y=x2x-y2.又点Q(t,-2)的坐标满足这两个方程,代入得-2=x1t-y1,-2=x2t-y2,则说明A(x1,y1),B(x2,y2)都满足方程-2=xt-y,即直线AB的方程为y-2=tx,因此直线AB恒过定点(0,2).
15.已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若·=12,其中O为坐标原点,求|MN|.
解 (1)由题设可知,直线l的方程为y=kx+1,
因为l与圆C交于两点,所以<1.
解得<k<.
所以k的取值范围为.
(2)设M(x1,y1),N(x2,y2),
将y=kx+1代入方程(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0.
所以x1+x2=,x1x2=.
·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1
=+8.
由题设可得+8=12,解得k=1,
所以l的方程为y=x+1.
故圆心C在l上,所以|MN|=2.
16.已知圆F1:(x+1)2+y2=r2与圆F2:(x-1)2+y2=(4-r)2 (0<r<4)的公共点的轨迹为曲线E,且曲线E与y轴的正半轴相交于点M.若曲线E上相异的两点A,B满足直线MA,MB的斜率之积为.
(1)求曲线E的方程;
(2)证明:直线AB恒过定点,并求定点的坐标;
(3)求△ABM的面积的最大值.
(1)解 设圆F1,圆F2的公共点为Q,
由已知得|F1F2|=2,|QF1|=r,|QF2|=4-r,
故|QF1|+|QF2|=4>|F1F2|,
因此曲线E是长轴长2a=4,焦距2c=2的椭圆,且b2=a2-c2=3,
所以曲线E的方程为+=1.
(2)证明 由曲线E的方程,得上顶点M(0,),记A(x1,y1),B(x2,y2),由题意知,x1≠0,x2≠0,若直线AB的斜率不存在,则直线AB的方程为x=x1,故y1=-y2,且y=y=3,因此kMA·kMB=·=-=,与已知不符,因此直线AB的斜率存在,设直线AB:y=kx+m,代入椭圆E的方程+=1,得(3+4k2)x2+8kmx+4(m2-3)=0.①
因为直线AB与曲线E有公共点A,B,
所以方程①有两个非零不等实根x1,x2,
所以x1+x2=-,x1x2=,
又kAM==,
kMB==,
由kAM·kBM=,
得4(kx1+m-)(kx2+m-)=x1x2,
即(4k2-1)x1x2+4k(m-)(x1+x2)+4(m-)2=0,
所以4(m2-3)(4k2-1)+4k(m-)(-8km)+4(m-)2(3+4k2)=0,
化简得m2-3m+6=0,故m=或m=2,
结合x1x2≠0知,m=2,即直线AB恒过定点N(0,2).
(3)解 由Δ>0且m=2得k<-或k>,
又S△ABM=|S△ANM-S△BNM|=|MN|·|x2-x1|
=
=
==≤,
当且仅当4k2-9=12,即k=±时,△ABM的面积最大,最大值为.