- 2021-07-01 发布 |
- 37.5 KB |
- 2页

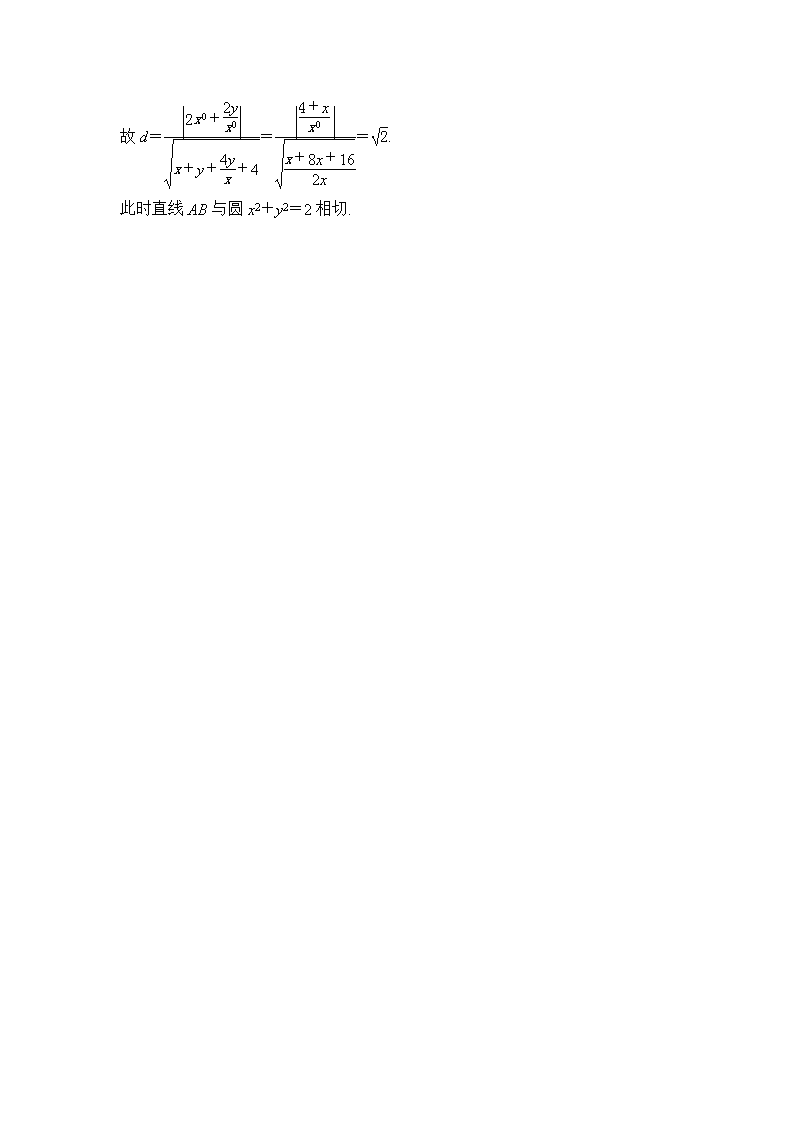
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017届高考数学(文)二轮复习(江苏专用)解答题+第三周+星期二
星期二 (解析几何问题) 2017年____月____日 已知椭圆C:x2+2y2=4. (1)求椭圆C的离心率; (2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,试判断直线AB与圆x2+y2=2的位置关系,并证明你的结论. 解 (1)由题意,椭圆C的标准方程为+=1. 所以a2=4,b2=2, 从而c2=a2-b2=2. 因此a=2,c=.故椭圆C的离心率e==. (2)直线AB与圆x2+y2=2相切.证明如下: 设点A,B的坐标分别为(x0,y0),(t,2), 其中x0≠0.因为OA⊥OB,所以·=0, 即tx0+2y0=0, 解得t=-. 当x0=t时,y0=-,代入椭圆C的方程,得t=±, 故直线AB的方程为x=±.圆心O到直线AB的距离d=.此时直线AB与圆x2+y2=2相切. 当x0≠t时,直线AB的方程为 y-2=(x-t), 即(y0-2)x-(x0-t)y+2x0-ty0=0. 圆心O到直线AB的距离d=. 又x+2y=4,t=-, 故d===. 此时直线AB与圆x2+y2=2相切.查看更多