山西省芮城市2020届高三3月月考数学（文）

山西省芮城市2020届高三3月月考数学（文）

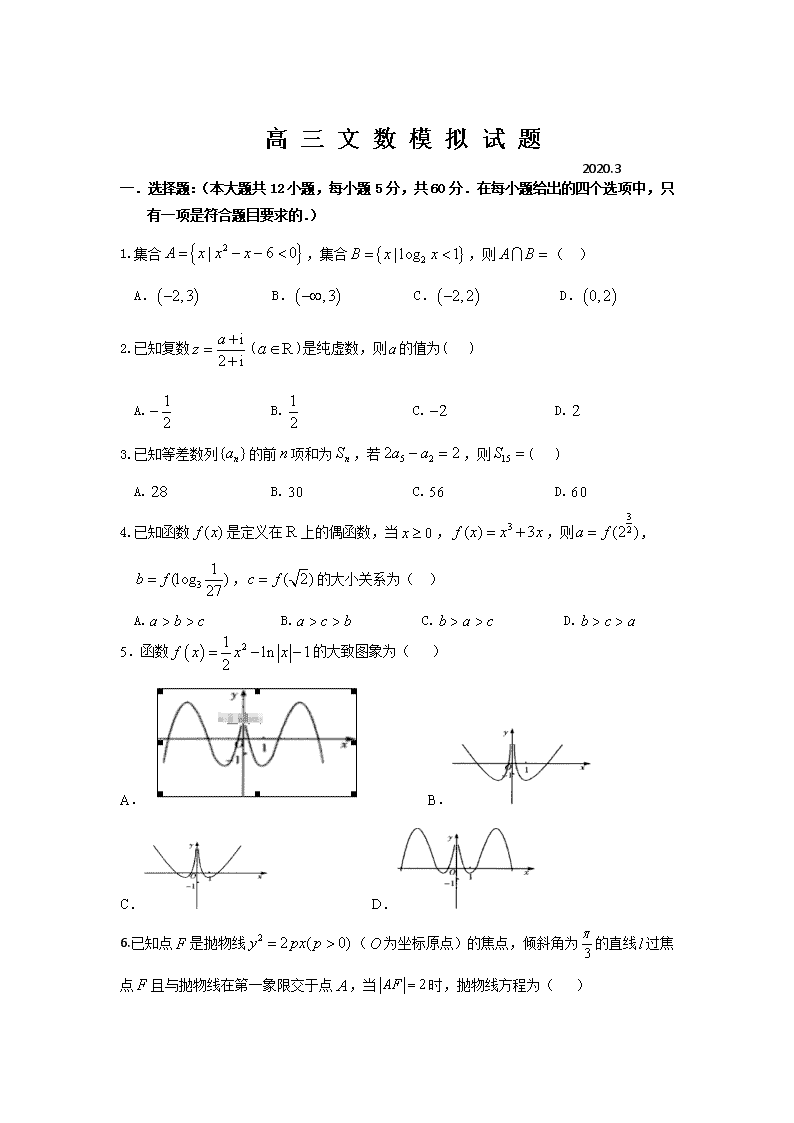
高 三 文 数 模 拟 试 题 ‎ 2020.3‎ 一．选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1.集合，集合，则（ ）‎ A． B． C． D．‎ ‎2.已知复数()是纯虚数，则的值为( )‎ A. B. C. D.‎ ‎3.已知等差数列的前项和为，若，则( )‎ A. B. C. D.‎ ‎4.已知函数是定义在上的偶函数，当，，则,，的大小关系为（ ）‎ A. B. C. D.‎ ‎5．函数的大致图象为（ ）‎ A． B．‎ C． D．‎ ‎6.已知点是抛物线（为坐标原点）的焦点，倾斜角为的直线过焦点且与抛物线在第一象限交于点，当时，抛物线方程为（ ）‎ A. B. C. D. ‎ ‎7.剪纸艺术是中国最古老的民间艺术之一，作为一种镂空艺术，它能给人以视觉上的艺术享受．在如图所示的圆形图案中有12个树叶状图形（即图中阴影部分），构成树叶状图形的圆弧均相同．若在圆内随机取一点，则此点取自阴影部分的概率是（　　）‎ A. B. C. D. ‎ y x ‎2‎ O ‎-2‎ ‎8.已知函数的部分图象如图所示，且，则的最小值为（　　）‎ A. B. ‎ C. D.‎ ‎9.我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升(注:一斗为十升).问,米几何?”下图是解决该问题的程序框图,执行该程序框图,若输出的S=15(单位:升),则输入的k的值为 (　　)‎ ‎ ‎ ‎ ‎ A. 45 B. 60 C. 75 D. 100‎ ‎10．在△ABC中，角A，B，C的对边分别为a，b，c，若＝，b＝4，则△ABC的面积的最大值为(　　)‎ A．4　　　 B．2　　 C．3　　 　 D． ‎11.已知、是双曲线： 的左、右焦点，若直线与双曲线在第一象限交于点，过向轴作垂线，垂足为，且为（为坐标原点）的中点，则该双曲线离心率为（ ）‎ A. B. C. D. ‎ ‎12.已知函数，若()，则的最大值为（ ） ‎ A. B. C. D.‎ 二．填空题：（本大题共4小题，每小题5分，共20分，请将答案填在答题卡上.）‎ ‎13.已知向量的夹角为，且，，则__________．‎ ‎14．某中学教学处采用系统抽样方法，从学校高三年级全体800名学生中抽50名学生做学习状况问卷调查．现将800名学生从1到800进行编号，在1至16号 中随机抽取一个数，如果抽到的是6，则从41至56号中应取的数是__________．‎ ‎15．已知，，则的值为__________．‎ ‎16.已知三棱锥中，底面，，，，，则该三棱锥的内切球的体积为__________．‎ 三、解答题：（本大题共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17.(本小题满分12分)‎ 某中学为了解中学生的课外阅读时间，决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生，对他们的课外阅读时间进行问卷调查．现在按课外阅读时间的情况将学生分成三类：类（不参加课外阅读），类（参加课外阅读，但平均每周参加课外阅读的时间不超过3小时），类（参加课外阅读，且平均每周参加课外阅读的时间超过3小时）．调查结果如下表：‎ 类 类 类 男生 ‎5‎ ‎3‎ 女生 ‎3‎ ‎3‎ ‎（1）求出表中，的值；‎ ‎（2）根据表中的统计数据，完成下面的列联表，并判断是否有90%的把握认为“参加课外阅读与否”与性别有关；‎ 男生 女生 总计 不参加课外阅读 参加课外阅读 总计 x0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎18.(本小题满分12分)‎ 已知等差数列的前项和为，公差，，且成等比数列.‎ ‎(1)求数列的通项公式及前项和；‎ P A B C E F G ‎(2)记，求数列的前项和.‎ ‎19.(本小题满分12分）‎ 如图，在三棱锥中，，，‎ ‎，，.‎ ‎(1)求证：平面平面； ‎ ‎(2)分别是棱的中点，为棱上的点，求三棱锥的体积.‎ ‎20.(本小题满分12分)‎ 已知函数.‎ ‎（1）若函数在点处的切线方程为，求实数的值；‎ ‎（2）当时，证明函数恰有一个零点.‎ ‎21.(本小题满分12分)‎ 已知动点P是△PMN的顶点，M（﹣2，0），N（2，0），直线PM，PN的斜率之积为﹣．‎ ‎（1）求点P的轨迹E的方程；‎ ‎（2）设四边形ABCD的顶点都在曲线E上，且AB∥CD，直线AB，CD分别过点 ‎（﹣1，0），（1，0），求四边形ABCD的面积为时，直线AB的方程．‎ 选考题：共10分.请考生在第22，23题中任选一题作答.如果多做，则按所做的第一题计分.选修4-4：坐标系与参数方程 ‎22．在直角坐标系中，直线，圆，以坐标原点为极点，轴正半轴为极轴建立极坐标系．‎ ‎（1）求、的极坐标方程；‎ ‎（2）若直线的极坐标方程为，设，的交点为，，求的面积．‎ 选修4-5：不等式选讲 ‎23.已知函数（其中）.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若关于的不等式恒成立，求的取值范围.‎ 高三文数模拟试题答案 一．1—6 DABCCB 7—12 BABADC 二．13. 14.54 15. 16 .‎ 三、解答题：（本大题共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17、【解答】：（1）设抽取的20人中，男，女生人数分别为，，则，，‎ 所以，；………6分 ‎（2）列联表如下：‎ 男生 女生 总计 不参加课外阅读 ‎4‎ ‎2‎ ‎6‎ 参加课外阅读 ‎8‎ ‎6‎ ‎14‎ 总计 ‎12‎ ‎8‎ ‎20‎ 的观测值，‎ 所以没有90%的把握认为“参加阅读与否”与性别有关；………12分 ‎18.解:(1)成等比数列，，，，解得或(舍去)………2分 ‎………4分 ‎………6分 ‎(2)由(Ⅰ)得，，………8分 ‎………10分 ‎………12分 ‎19.解:(1)证明：在中，由余弦定理得 ‎，即………2分 又，，，………3分 又，，，平面………4分 平面，平面平面………6分 ‎(2)， ………8分 分别是棱的中点，，………10分 ‎………12分 ‎20.（1）.‎ 由切线的斜率为得. ∴.………4分 ‎（2） ，，‎ ‎∴ .‎ ‎1.当时，‎ 由得或，得，‎ ‎∴在上递增，在上递减，在上递增.‎ 又 ，‎ ‎，‎ ‎∴当时函数恰有一个零点.………7分 ‎2.当时，‎ 恒成立，在上递增.‎ 又，，‎ 所以当时函数恰有一个零点.………9分 ‎3.当时，‎ 由得或，得，‎ ‎∴在上递增，在上递减，在上递增.‎ 又，‎ ‎，‎ ‎∴当时函数恰有一个零点.‎ 综上，当时，函数恰有一个零点.………12分 ‎21．解：（1）设点P（x，y），‎ ‎∵直线PM与PN的斜率之积为﹣，‎ 即＝＝﹣，‎ 化简得（x≠±2），‎ ‎∴动点P的轨迹E的方程为（x≠±2）；………4分 ‎（2）设直线AB的方程为x＝my﹣1，A（x1，y1），B（x2，y2），‎ 由 得（3m2+4）y2﹣6my﹣9＝0，‎ 则 , y1+y2＝，，………6分 ‎|y1﹣y2|＝＝，‎ ‎∴|AB|＝＝，‎ 又原点O到直线AB的距离d＝，‎ ‎∴S△ABO＝×＝，………8分 由图形的对称性可知，SABCD＝4S△ABO，‎ ‎∴SABCD＝＝，‎ 化简得18m4﹣m2﹣17＝0，………10分 解得m2＝1，即m＝±1，‎ ‎∴直线AB的方程为x＝±y﹣1，即x±y+1＝0．………12分 ‎22．解：（1）因为，‎ ‎∴的极坐标方程为………2分 的极坐标方程为．………5分 ‎（2）将代入，‎ 得，解得，，‎ ‎，………8分 因为的半径为1，则的面积．………10分 ‎23.解：（1）方法一：当时，函数，‎ 则不等式为，‎ ‎①当时，原不等式为，解得：；‎ ‎②当时，原不等式为，解得：.此时不等式无解；‎ ‎③当时，原不等式为，解得：，‎ 原不等式的解集为.………5分 方法二：当时，函数 ，画出函数的图象，如图：‎ 结合图象可得原不等式的解集为.………5分 ‎（2）不等式即为 ，‎ 即关于的不等式恒成立.‎ 而 ，‎ 所以，‎ 解得或，‎ 解得或.‎ 所以的取值范围是.………10分