- 2021-07-01 发布 |
- 37.5 KB |
- 16页


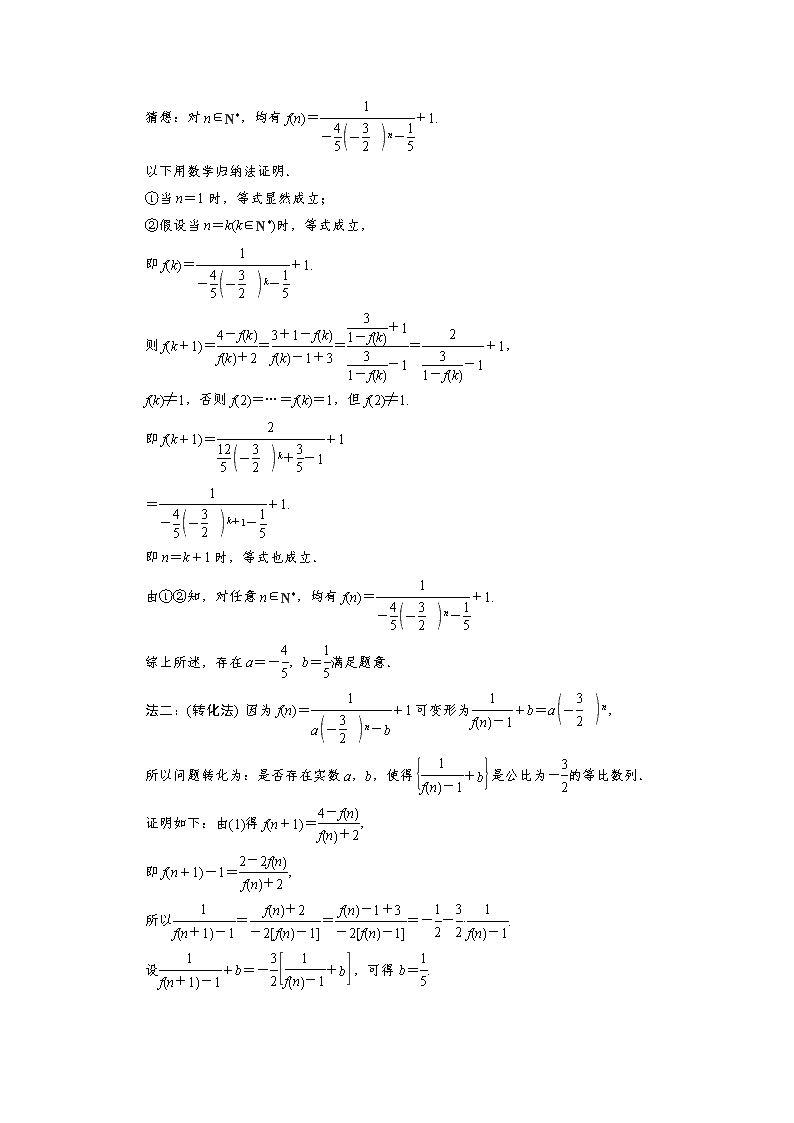
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习苏教版专题八第二讲数学归纳法学案
第二讲 数学归纳法 题型(一) 用数学归纳法证明等式 主要考查利用数学归纳法证明与正整数有关的代数等式. [典例感悟] [例1] 设|θ|<,n为正整数,数列{an}的通项公式an=sintannθ,其前n项和为Sn. (1)求证:当n为偶数时,an=0;当n为奇数时,an=(-1)tannθ; (2)求证:对任何正整数n,S2n=sin 2θ·[1+(-1)n+1tan2nθ]. [证明] (1)因为an=sintannθ. 当n为偶数时,设n=2k,k∈N*,an=a2k=sintan2kθ=sin kπ·tan2kθ=0,an=0. 当n为奇数时,设n=2k-1,k∈N*,an=a2k-1=sintannθ=sin·tannθ. 当k=2m,m∈N*时,an=a2k-1=sin·tannθ=sin·tannθ=-tannθ, 此时=2m-1,an=a2k-1=-tannθ=(-1)2m-1·tannθ=(-1)tannθ. 当k=2m-1,m∈N*时,an=a2k-1=sin·tannθ=sin·tannθ=tannθ, 此时=2m-2,an=a2k-1=tannθ=(-1)2m-2·tannθ=(-1)tannθ. 综上,当n为偶数时,an=0;当n为奇数时,an=(-1)tannθ. (2)当n=1时,由(1)得,S2=a1+a2=tan θ, 等式右边=sin 2θ(1+tan2θ)=sin θ·cos θ·=tan θ. 故n=1时,命题成立, 假设n=k(k∈N*,k≥1)时命题成立, 即S2k=sin 2θ·[1+(-1)k+1tan2kθ]. 当n=k+1时,由(1)得: S2(k+1)=S2k+a2k+1+a2k+2=S2k+a2k+1=sin 2θ·+(-1)ktan2k+1θ=sin 2θ·= sin 2θ·= sin 2θ·=sin 2θ·[1+(-1)k+2·tan2k+2θ ]. 即当n=k+1时命题成立. 综上所述,对任何正整数n,S2n=sin 2θ·[1+(-1)n+1tan2nθ]. [方法技巧] (1)用数学归纳法证明等式问题是常见题型,其关键点在于弄清等式两边的构成规律,等式两边各有多少项,以及初始值n0的值. (2)由n=k到n=k+1时,除考虑等式两边变化的项外还要充分利用n=k时的式子,即充分利用假设,正确写出归纳证明的步骤,从而使问题得以证明. [演练冲关] (2018·苏州期末)在正整数集N*上定义函数y=f(n),满足f(n)[f(n+1)+1]=2[2-f(n+1)],且f(1)=2. (1)求证:f(3)-f(2)=; (2)是否存在实数a,b,使得f(n)=+1对任意正整数n恒成立,并证明你的结论. 解:(1)证明:由f(n)[f(n+1)+1]=2[2-f(n+1)],变形得f(n+1)=. 由f(1)=2,得f(2)=,再得f(3)=. 所以f(3)-f(2)=-=. (2)法一:(数学归纳法)由f(2)=,f(3)=,可得a=-,b=. 猜想:对n∈N*,均有f(n)=+1. 以下用数学归纳法证明. ①当n=1时,等式显然成立; ②假设当n=k(k∈N*)时,等式成立, 即f(k)=+1. 则f(k+1)====+1, f(k)≠1,否则f(2)=…=f(k)=1,但f(2)≠1. 即f(k+1)=+1 =+1. 即n=k+1时,等式也成立. 由①②知,对任意n∈N*,均有f(n)=+1. 综上所述,存在a=-,b=满足题意. 法二:(转化法) 因为f(n)=+1可变形为+b=an, 所以问题转化为:是否存在实数a,b,使得是公比为-的等比数列. 证明如下:由(1)得f(n+1)=, 即f(n+1)-1=, 所以===--·. 设+b=-,可得b=. 所以是首项为+=,公比为-的等比数列. 通项公式为+=n-1, 所以f(n)=+1. 综上所述,存在a=-,b=满足题意. 题型(二) 用数学归纳法证明不等式 主要考查用数学归纳法证明与正整数有关的不等式. [典例感悟] [例2] (2018·南京模拟)已知数列{an}满足an=3n-2,函数f(n)=++…+,g(n)=f(n2)-f(n-1),n∈N*. (1)求证:g(2)>; (2)求证:当n≥3时,g(n)> . [证明] (1)由题意知,an=3n-2, g(n)=+++…+, 当n=2时,g(2)=++=++=>.故结论成立. (2)用数学归纳法证明: ①当n=3时,g(3)=+++…+=++++++=++>++ =++>++>, 所以当n=3时,结论成立. ②假设当n=k(k≥3,k∈N*)时,结论成立, 即g(k)>, 则当n=k+1时,g(k+1)=g(k)+++…+->+++…+->+- =+ =+, 由k≥3可知,3k2-7k-3>0,即g(k+1)>. 所以当n=k+1时,结论也成立. 综合①②可得,当n≥3时,g(n)>. [方法技巧] (1)当遇到与正整数n有关的不等式证明时,应用其他办法不容易证,则可考虑应用数学归纳法. (2)用数学归纳法证明不等式的关键是由n=k(k∈N*)成立,推证n=k+1时也成立,证明时用上归纳假设后,可采用分析法、综合法、作差(作商)比较法、放缩法等证明. [演练冲关] 设fn(x)是等比数列1,x,x2,…,xn的和,其中x>0,n∈N,n≥2. (1)证明:函数Fn(x)=fn(x)-2在内有且仅有一个零点(记为xn),且xn=+x; (2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)和 gn(x)的大小,并加以证明. 解:(1)证明:Fn(x)=fn(x)-2=1+x+x2+…+xn-2, 则Fn(1)=n-1>0, Fn=1++2+…+n-2 =-2=-<0, 所以Fn(x)在内至少存在一个零点. 又Fn′(x)=1+2x+…+nxn-1>0, 故Fn(x)在内单调递增, 所以Fn(x)在内有且仅有一个零点xn. 因为xn是Fn(x)的零点,所以Fn(xn)=0, 即-2=0,故xn=+x. (2)由题设,fn(x)=1+x+x2+…+xn, gn(x)=,x>0. 当x=1时,fn(x)=gn(x). 当x≠1时,用数学归纳法可以证明fn(x)<gn(x). ①当n=2时,f2(x)-g2(x)=-(1-x)2<0, 所以f2(x)<g2(x)成立. ②假设n=k(k≥2,k∈N*)时,不等式成立, 即fk(x)<gk(x). 那么,当n=k+1时, fk+1(x)=fk(x)+xk+1<gk(x)+xk+1 =+xk+1=. 又gk+1(x)- =, 令hk(x)=kxk+1-(k+1)xk+1(x>0), 则h′k(x)=k(k+1)xk-k(k+1)xk-1 =k(k+1)xk-1·(x-1). 所以当0<x<1时,h′k(x)<0,hk(x)在(0,1)上递减; 当x>1时,h′k(x)>0,hk(x)在(1,+∞)上递增. 所以hk(x)>hk(1)=0, 从而gk+1(x)>. 故fk+1(x)<gk+1(x),即n=k+1时不等式也成立. 由①和②知,对一切n≥2的整数,都有fn(x)<gn(x). 综上可知,当x=1时,fn(x)=gn(x); 当x≠1时,对一切n≥2的整数,fn(x)查看更多
相关文章
- 当前文档收益归属上传用户