2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数（练）（解析版）

2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数（练）（解析版）

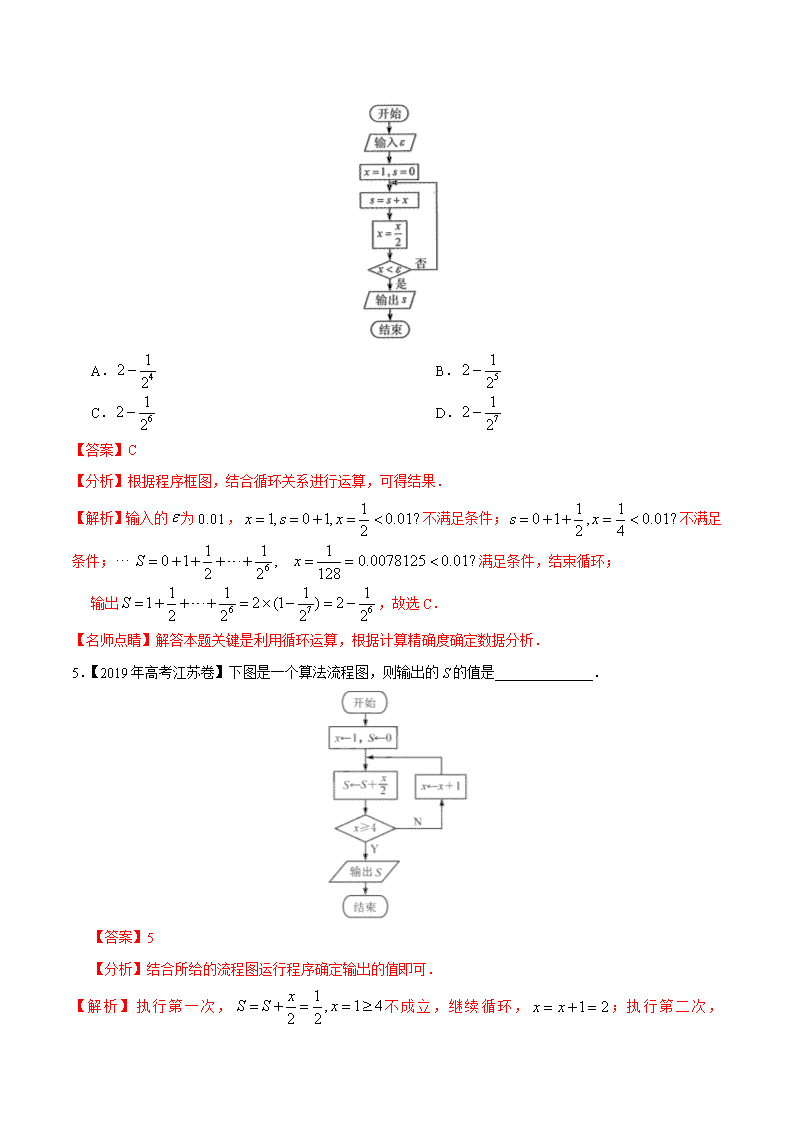
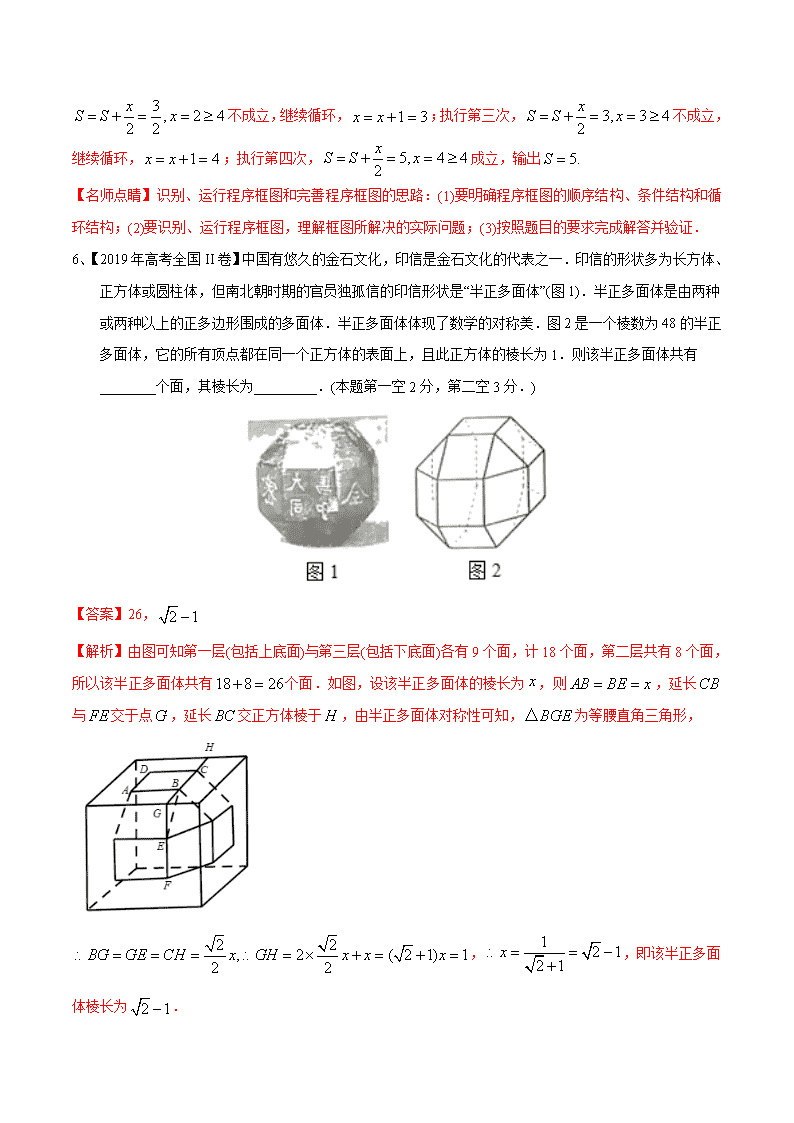
专题13 算法、推理与证明、复数 ‎1．【2019年高考天津卷】是虚数单位，则的值为______________．‎ ‎【答案】‎ ‎【分析】先化简复数，再利用复数模的定义求所给复数的模．‎ ‎【解析】由题可得．‎ ‎2．【2019年高考浙江卷】复数(为虚数单位)，则=______________．‎ ‎【答案】‎ ‎【分析】本题先计算，而后求其模.或直接利用模的性质计算. 容易题，注重基础知识、运算求解能力的考查．‎ ‎【解析】由题可得．‎ ‎3．【2019年高考江苏卷】已知复数的实部为0，其中为虚数单位，则实数a的值是______________．‎ ‎【答案】‎ ‎【分析】本题根据复数的乘法运算法则先求得，然后根据复数的概念，令实部为0即得a的值．‎ ‎【解析】由题可得，令，解得．‎ ‎【名师点睛】本题主要考查复数的运算法则，虚部的定义等知识，意在考查学生的转化能力和计算求解能力．‎ ‎4、【2019年高考全国Ⅲ卷】执行下边的程序框图，如果输入的为0．01，则输出的值等于 A． B．‎ C． D．‎ ‎【答案】C ‎【分析】根据程序框图，结合循环关系进行运算，可得结果．‎ ‎【解析】输入的为，不满足条件；不满足条件；满足条件，结束循环；‎ 输出，故选C．‎ ‎【名师点睛】解答本题关键是利用循环运算，根据计算精确度确定数据分析．‎ ‎5．【2019年高考江苏卷】下图是一个算法流程图，则输出的S的值是______________．‎ ‎【答案】5‎ ‎【分析】结合所给的流程图运行程序确定输出的值即可．‎ ‎【解析】执行第一次，不成立，继续循环，；执行第二次，‎ 不成立，继续循环，；执行第三次，不成立，继续循环，；执行第四次，成立，输出 ‎【名师点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构；(2)要识别、运行程序框图，理解框图所解决的实际问题；(3)按照题目的要求完成解答并验证．‎ ‎6、【2019年高考全国II卷】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1)．半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．(本题第一空2分，第二空3分．)‎ ‎【答案】26，‎ ‎【解析】由图可知第一层(包括上底面)与第三层(包括下底面)各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有个面．如图，设该半正多面体的棱长为，则，延长与交于点，延长交正方体棱于，由半正多面体对称性可知，为等腰直角三角形，‎ ‎，，即该半正多面体棱长为．‎ ‎【名师点睛】本题立意新颖，空间想象能力要求高，物体位置还原是关键，遇到新题别慌乱，题目其实很简单，稳中求胜是关键．立体几何平面化，无论多难都不怕，强大空间想象能力，快速还原图形．‎ 例、某同学准备用反证法证明如下一个问题：函数f(x)在[0,1]上有意义，且f(0)＝f(1)，如果对于不同的 x1，x2∈[0,1]，都有|f(x1)－f(x2)|<|x1－x2|，求证：|f(x1)－f(x2)|<.那么他的反设应该是________．‎ 答案：“存在x1，x2∈[0,1]，使得|f(x1)－f(x2)|<|x1－x2|，则|f(x1)－f(x2)|≥”‎ 例、已知a1＋a2＋a3＋a4>100，求证：a1，a2，a3，a4中至少有一个数大于25.‎ 证明：假设a1，a2，a3，a4均不大于25，即a1≤25，a2≤25，a3≤25，a4≤25，‎ 则a1＋a2＋a3＋a4≤25＋25＋25＋25＝100，‎ 这与已知a1＋a2＋a3＋a4>100矛盾，故假设错误．‎ 所以a1，a2，a3，a4中至少有一个数大于25.‎ 例、已知f(x)＝ax2＋bx＋c，若a＋c＝0，f(x)在[－1,1]上的最大值为2，最小值为－.求证：a≠0且<2.‎ 证明：假设a＝0或≥2.‎ ‎(1)当a＝0时，由a＋c＝0，得f(x)＝bx，显然b≠0.由题意得f(x)＝bx在[－1,1]上是单调函数，‎ 所以f(x)的最大值为|b|，最小值为－|b|.由已知条件，得|b|＋(－|b|)＝2－＝－，‎ 这与|b|＋(－|b|)＝0相矛盾，所以a≠0.‎ ‎(2)当≥2时，由二次函数的对称轴为x＝－，知f(x)在[－1,1]上是单调函数，故其最值在区间的端点处取得．所以或 又a＋c＝0，则此时b无解，所以<2. 由(1)(2)，得a≠0且<2.‎ ‎1、【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2020届高三调研】下图是一个算法流程图．若输出的值为4，则输入的值为______________．‎ ‎【答案】‎ ‎【解析】当时，由流程图得，令，解得，满足题意．当时，由流程图得，令，解得，不满足题意．故输入的值为．‎ ‎2．【北京市人大附中2020届高三高考信息卷(三)】执行如图所示的程序框图，若输入值满足，则输出值的取值范围是______________．‎ ‎【答案】‎ ‎【解析】根据输入值满足，利用函数的定义域，分成两部分：即和，当时，执行 的关系式，故，当时，执行的关系式，故．综上所述：，故输出值的取值范围是．‎ ‎3．【江西省新八校2020届高三第二次联考】如图所示的程序框图所实现的功能是 A．输入的值，计算的值 B．输入的值，计算的值 C．输入的值，计算的值 D．输入的值，计算的值 ‎【答案】B ‎【解析】由程序框图，可知，，由的初值为，末值为，可知，此递推公式共执行了次，又由，得，得 即，故，故选B．‎ ‎4．【河南省郑州市2020届高三第三次质量检测】已知，则 A． B．‎ C． D．‎ ‎【答案】D ‎【分析】先根据复数的运算，求得复数z，再求其模长的平方即可．‎ ‎【解析】因为，所以，故选D．‎ ‎【名师点睛】本题考查了复数的知识点，懂的运算求得模长是解题的关键，属于基础题．‎ ‎5．【山东省烟台市2020届高三5月考)】复数在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【答案】D ‎【解析】由题可得，则在复平面内对应的点为，位于第四象限．故选D．‎ ‎6．【福建省厦门第一中学2020届高三模拟】已知为虚数单位，若，则 A．1 B．‎ C． D．2‎ ‎【答案】C ‎【解析】因为为虚数单位，，所以，根据复数相等可得，所以．故选C．‎ ‎【名师点睛】本题考查了复数除法运算，以及复数相等的概念，复数与相等的充要条件是且．复数相等的充要条件是化复为实的主要依据，多用来求解参数的值或取值范围．步骤是：分别分离出两个复数的实部和虚部，利用实部与实部相等、虚部与虚部相等列方程(组)求解．‎ ‎7．【四川省宜宾市2020届高三诊断】欧拉公式：为虚数单位)，由瑞士数学家欧拉发明，它建立了三角函数与指数函数的关系，根据欧拉公式，‎ A．1 B．‎ C． D．‎ ‎【答案】B ‎【分析】由题意将复数的指数形式化为三角函数式，再由复数的运算化简即可得答案。‎ ‎【解析】由，得，故选B．‎ ‎【名师点睛】本题考查欧拉公式的应用，考查三角函数值的求法与复数的化简求值，是基础题．‎ ‎8．(2020·宁波模拟)分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证0　　　　　 　　　 B．a－c>0‎ C．(a－b)(a－c)>0 D．(a－b)(a－c)<0‎ ‎【答案】C ‎【解析】0⇔(a－c)(2a＋c)>0⇔(a－c)(a－b)>0.‎ ‎9．【陕西省延安市2020届高考模拟试题数学】甲、乙、丙三位教师分别在延安、咸阳、宝鸡的三所中学里教不同的学科，已知：‎ ‎①甲不在延安工作，乙不在咸阳工作；‎ ‎②在延安工作的教师不教学科；‎ ‎③在咸阳工作的教师教学科；‎ ‎④乙不教学科.‎ 可以判断乙工作的地方和教的学科分别是______、_____．‎ ‎【答案】宝鸡， ‎ ‎【解析】由③得在咸阳工作的教师教A学科；又由①得乙不在咸阳工作，所以乙不教A学科；‎ 由④得乙不教B学科，结合③乙不教A学科，可得乙必教C学科，‎ 所以由②得乙不在延安工作，由①得乙不在咸阳工作；所以乙在宝鸡工作，‎ 综上，乙工作地方和教的学科分别是宝鸡和C学科．‎ 故答案为：宝鸡，C．‎ ‎【名师点睛】本题考查简单的合理推理，考查逻辑推理能力，是基础题．‎ ‎10．观察下列式子：1,1＋2＋1,1＋2＋3＋2＋1,1＋2＋3＋4＋3＋2＋1，…，由以上可推测出一个一般性结论：对于n∈N*,1＋2＋…＋n＋…＋2＋1＝________.‎ ‎【答案】n2‎ ‎【解析】∵1＝12,1＋2＋1＝22,1＋2＋3＋2＋1＝32,1＋2＋3＋4＋3＋2＋1＝42，…，‎ ‎∴归纳可得1＋2＋…＋n＋…＋2＋1＝n2.‎