2018届二轮复习（文）专题五立体几何3

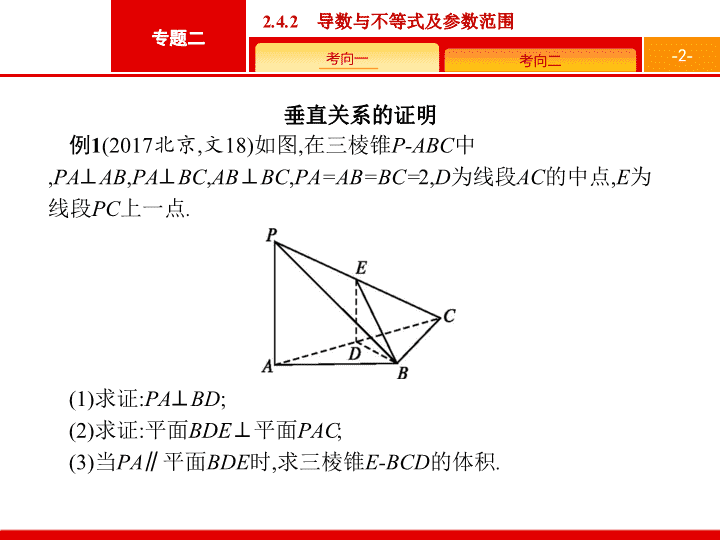
2018届二轮复习（文）专题五立体几何3

5 . 3 . 2 　 空间中的垂直、夹角 及 几何体 的体积 - 2 - 垂直关系的证明 例 1 (2017 北京 , 文 18) 如图 , 在三棱锥 P-ABC 中 , PA ⊥ AB , PA ⊥ BC , AB ⊥ BC , PA=AB=BC= 2, D 为线段 AC 的中点 , E 为线段 PC 上一点 . (1) 求证 : PA ⊥ BD ; (2) 求证 : 平面 BDE ⊥ 平面 PAC ; (3) 当 PA ∥ 平面 BDE 时 , 求三棱锥 E-BCD 的体积 . - 3 - (1) 证明 因为 PA ⊥ AB , PA ⊥ BC , 所以 PA ⊥ 平面 ABC. 又因为 BD ⊂ 平面 ABC , 所以 PA ⊥ BD. (2) 证明 因为 AB=BC , D 为 AC 中点 , 所以 BD ⊥ AC. 由 (1) 知 , PA ⊥ BD , 所以 BD ⊥ 平面 PAC. 所以平面 BDE ⊥ 平面 PAC. (3) 解 因为 PA ∥ 平面 BDE , 平面 PAC ∩ 平面 BDE=DE , 所以 PA ∥ DE. 因为 D 为 AC 的中点 , 解题心得 从解题方法上讲 , 由于线线垂直、线面垂直、面面垂直之间可以相互转化 , 因此整个解题过程始终沿着线线垂直、线面垂直、面面垂直的转化途径进行 . - 4 - 对点训练 1 (2017 全国 Ⅲ , 文 19) 如图 , 四面体 ABCD 中 , △ ABC 是正三角形 , AD=CD . (1) 证明 : AC ⊥ BD ; (2) 已知 △ ACD 是直角三角形 , AB=BD , 若 E 为棱 BD 上与 D 不重合的点 , 且 AE ⊥ EC , 求四面体 ABCE 与四面体 ACDE 的体积比 . - 5 - 解 (1) 取 AC 的中点 O , 连接 DO , BO . 因为 AD=CD , 所以 AC ⊥ DO. 又由于 △ ABC 是正三角形 , 所以 AC ⊥ BO. 从而 AC ⊥ 平面 DOB , 故 AC ⊥ BD. - 6 - (2) 连接 EO. 由 (1) 及题设知 ∠ ADC= 90°, 所以 DO=AO. 在 Rt △ AOB 中 , BO 2 +AO 2 =AB 2 . 又 AB=BD , 所以 BO 2 +DO 2 =BO 2 +AO 2 =AB 2 =BD 2 , 故 ∠ DOB= 90° . 故 E 为 BD 的中点 , 从而 E 到平面 ABC 的距离为 D 到平面 ABC 的距离 的 , 四面体 ABCE 的体积为四面体 ABCD 的体积 的 , 即四面体 ABCE 与四面体 ACDE 的体积之比为 1 ∶ 1 . - 7 - 平面图形的折叠问题 例 2 如图 , 菱形 ABCD 的对角线 AC 与 BD 交于点 O , 点 E , F 分别在 AD , CD 上 , AE=CF , EF 交 BD 于点 H. 将 △ DEF 沿 EF 折到 △ D'EF 的位置 . (1) 证明 : AC ⊥ HD' ; - 8 - (1) 证明 由已知得 AC ⊥ BD , AD=CD . 由此得 EF ⊥ HD , EF ⊥ HD' , 所以 AC ⊥ HD '. 故 OD' ⊥ OH. 由 (1) 知 AC ⊥ HD' , 又 AC ⊥ BD , BD ∩ HD'=H , 所以 AC ⊥ 平面 BHD' , 于是 AC ⊥ OD'. 又由 OD' ⊥ OH , AC ∩ OH=O , 所以 , OD' ⊥ 平面 ABC. - 9 - 解题心得 平面图形经过翻折成为空间图形后 , 原有的性质有的发生变化 , 有的没变 . 一般地 , 在翻折后还在一个平面上的性质不发生变化 , 不在同一个平面上的性质可能发生变化 . 解决这类问题就是要根据这些变与不变 , 去研究翻折以后的空间图形中的线面关系和各类几何量的度量值 , 这是化解翻折问题的主要方法 . - 10 - 对点训练 2 (2017 宁夏银川二模 , 文 19) 如图 1, 菱形 ABCD 的边长为 12, ∠ BAD= 60°, AC 交 BD 于点 O. 将菱形 ABCD 沿对角线 AC 折起 , 得到三棱锥 B-ACD , 点 M , N 分别是棱 BC , AD 的中点 , 且 DM= 6 . ( 1) 求证 : OD ⊥ 平面 ABC ; (2) 求三棱锥 M-ABN 的体积 . - 11 - (1) 证明 ∵ 四边形 ABCD 是菱形 , ∴ AD=DC , OD ⊥ AC. 在 △ ADC 中 , AD=DC= 12, ∠ ADC= 120°, 则 OD= 6 . ∵ OD 2 +OM 2 =MD 2 , ∴ DO ⊥ OM. ∵ OM , AC ⊂ 平面 ABC , OM ∩ AC=O , ∴ OD ⊥ 平面 ABC. - 12 - (2) 解 取 线段 AO 的中点 E , 连接 NE. ∵ N 是棱 AD 的中点 , 由 (1) 得 OD ⊥ 平面 ABC , ∴ NE ⊥ 平面 ABC. 在 △ ABM 中 , AB= 12, BM= 6, ∠ ABM= 120°, - 13 - 几何体中的作图问题 例 3 如 图 , 已知正三棱锥 P-ABC 的侧面是直角三角形 , PA= 6 . 顶点 P 在平面 ABC 内的正投影为点 D , D 在平面 PAB 内的正投影为点 E , 连接 PE 并延长交 AB 于点 G . (1) 证明 : G 是 AB 的中点 ; (2) 在图中作出点 E 在平面 PAC 内的正投影 F ( 说明作法及理由 ), 并求四面体 PDEF 的体积 . - 14 - (1) 证明 因为 P 在平面 ABC 内的正投影为 D , 所以 AB ⊥ PD. 因为 D 在平面 PAB 内的正投影为 E , 所以 AB ⊥ DE. 所以 AB ⊥ 平面 PED , 故 AB ⊥ PG. 又由已知可得 , PA=PB , 从而 G 是 AB 的中点 . (2) 解 在 平面 PAB 内 , 过点 E 作 PB 的平行线交 PA 于点 F , F 即为 E 在平面 PAC 内的正投影 . 理由 如下 : 由已知可得 PB ⊥ PA , PB ⊥ PC , 又 EF ∥ PB , 所以 EF ⊥ PA , EF ⊥ PC. - 15 - 因此 EF ⊥ 平面 PAC , 即点 F 为 E 在平面 PAC 内的正投影 . 连接 CG , 因为 P 在平面 ABC 内的正投影为 D , 所以 D 是正三角形 ABC 的中心 . 由 (1) 知 , G 是 AB 的中点 , 所以 D 在 CG 上 , 由已知 , 正三棱锥的侧面是直角三角形且 PA= 6, 可得 DE= 2, PE= 2 . 在等腰直角三角形 EFP 中 , 可得 EF=PF= 2 . - 16 - 解题心得 解立体几何题 , 总是离不开作辅助直线、辅助平面 . 而作好图形的基础在于基本作图 : 基本作图如 : (1) 过不在同一条直线上的三点作一个平面 ; (2) 作已知两个相交平面的交线等 . - 17 - 对点训练 3 如 图 , 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , AB= 16, BC= 10, AA 1 = 8, 点 E , F 分别在 A 1 B 1 , D 1 C 1 上 , A 1 E=D 1 F= 4, 过点 E , F 的平面 α 与此长方体的面相交 , 交线围成一个正方形 . ( 1) 在图中画出这个正方形 ( 不必说明画法和理由 ); (2) 求平面 α 把该长方体分成的两部分体积的比值 . - 18 - 解 (1) 交线围成的正方形 EHGF 如图 : (2) 作 EM ⊥ AB , 垂足为 M , 则 AM=A 1 E= 4, EB 1 = 12, EM=AA 1 = 8 . 因为四边形 EHGF 为正方形 , 所以 EH=EF=BC= 10 . - 19 - 空间中的角 例 4 (2017 天津 , 文 17 ) 如 图 , 在四棱锥 P-ABCD 中 , AD ⊥ 平面 PDC , AD ∥ BC , PD ⊥ PB , AD= 1, BC= 3, CD= 4, PD= 2 . ( 1) 求异面直线 AP 与 BC 所成角的余弦值 ; (2) 求证 : PD ⊥ 平面 PBC ; (3) 求直线 AB 与平面 PBC 所成角的正弦值 . - 20 - (1) 解 如图 , 由已知 AD ∥ BC , 故 ∠ DAP 或其补角即为异面直线 AP 与 BC 所成的角 . 因为 AD ⊥ 平面 PDC , 所以 AD ⊥ PD. (2) 证明 因为 AD ⊥ 平面 PDC , 直线 PD ⊂ 平面 PDC , 所以 AD ⊥ PD. 又因为 BC ∥ AD , 所以 PD ⊥ BC. 又 PD ⊥ PB , 所以 PD ⊥ 平面 PBC. - 21 - (3) 解 过点 D 作 AB 的平行线交 BC 于点 F , 连接 PF , 则 DF 与平面 PBC 所成的角等于 AB 与平面 PBC 所成的角 . 因为 PD ⊥ 平面 PBC , 故 PF 为 DF 在平面 PBC 上的射影 , 所以 ∠ DFP 为直线 DF 和平面 PBC 所成的角 . 由于 AD ∥ BC , DF ∥ AB , 故 BF=AD= 1, 由已知 , 得 CF=BC-BF= 2 . 又 AD ⊥ DC , 故 BC ⊥ DC , - 22 - 解题心得 空间中的角包括异面直线所成的角、线与面所成的角及二面角 . 求空间中的角的步骤是一作 , 二证 , 三求 . 如何作出所求角是关键 , 异面直线所成的角一般利用平行线转化为同一平面内的两条直线所成的角 ; 线与面所成的角一般找到直线在平面内的射影 , 转化为直线与直线在平面内的射影所成的角 ; 求二面角转化为求二面角的平面角 . - 23 - 对点训练 4 (2017 河北武邑中学三模 , 文 18 ) 如 图 , DC ⊥ 平面 ABC , EB ∥ DC , AC=BC=EB= 2 DC= 2, ∠ ACB= 120°, P , Q 分别为 AE , AB 的中点 . (1) 证明 : P Q ∥ 平面 ACD ; (2) 求 AD 与平面 ABE 所成角的正弦值 . - 24 - (1) 证明 连接 DP , CQ , 在 △ ABE 中 , ∵ P , Q 分别是 AE , AB 的中点 , ∴ PQ