【数学】2019届一轮复习北师大版客观题的解题方法与技巧学案

【数学】2019届一轮复习北师大版客观题的解题方法与技巧学案

客观题包括选择题与填空题，全国卷中共设置12道选择题，4道填空题，每题均为5分，共80分，占总分的53，3 ，在解题方法上与一般的解答题没有本质的区别，其不同之处在于选择题、填空题只看最后结果，不要解答过程，不管使用什么样的方法只要把结果做对，就算成功地解答了一个选择题、填空题，特别是选择题还有选项可以参照，其解法更具有一定的技巧性，快速准确地解决客观题，可使自己有比较足够的时间解决解答题，提高自己的总成绩，客观题解法多样，从大的方面看，解答客观题的主要策略是直接求解和间接求解。‎ 解题策略一　直接求解 直接求解是根据试题的已知条件，通过计算、推理等得出结果的方法，常用的有 综合法、数形结合法和等价转化法等，‎ 方法1　综合法 ‎【例1】 (2017·全国Ⅰ卷)设x，y， 为正数，且2x=3y=5 ，则(　　)‎ ‎(A)2x<3y<5 (B)5 <2x<3y ‎(C)3y<5 <2x (D)3y<2x<5 ‎ ‎【思维建模】 综合法关键是根据已知条件进行正确的运算和推理，直至得出结果，但选择题有选项作参照，可以校验解题过程的正误， ‎ ‎【变式探究】(2017·全国Ⅱ卷)若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点，则f(x)的极小值为(　　)‎ ‎(A)-1 (B)-2e-3 (C)5e-3 (D)1‎ ‎【解析】f′(x)=[x2+(a+2)x+a-1]·ex-1，‎ 则f′(-2)=[4-2(a+2)+a-1]·e-3=0，解得a=-1，‎ 则f(x)=(x2-x-1)·ex-1， ‎ f′(x)=(x2+x-2)·ex-1，‎ 令f′(x)=0，得x=-2或x=1，‎ 当x<-2或x>1时，f′(x) >0，‎ 当-2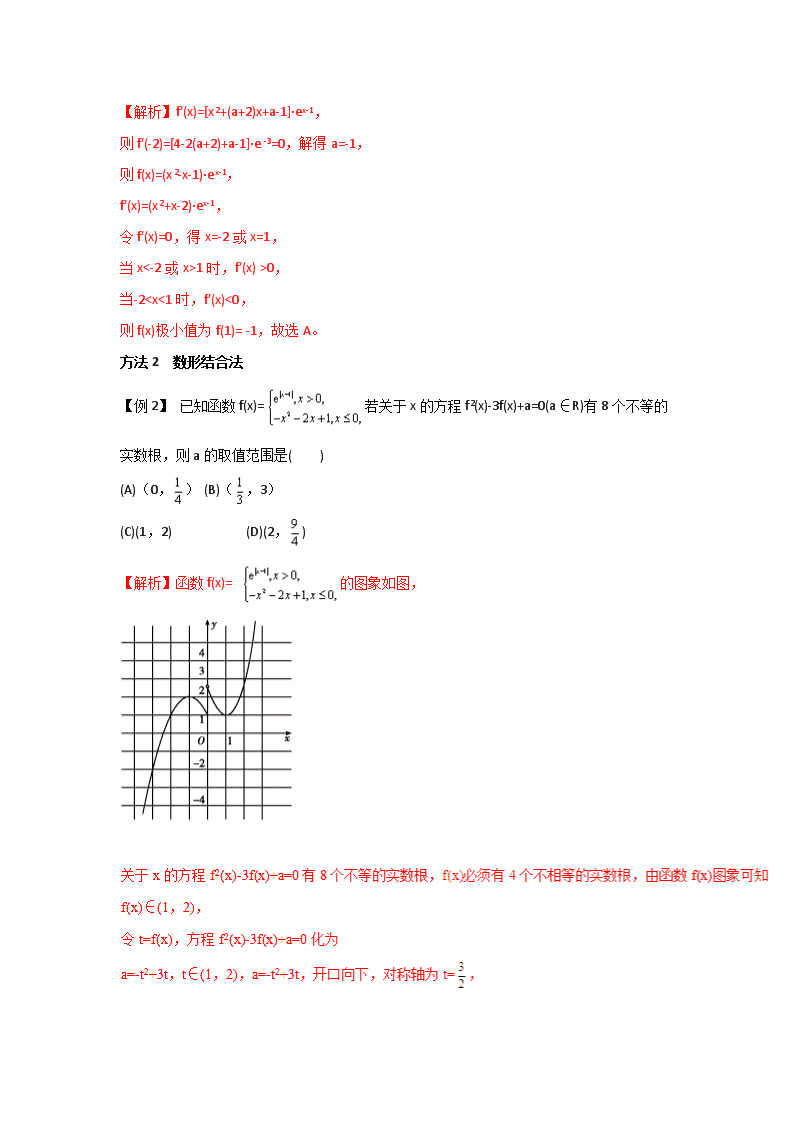g(x2)恒成立，则mg(x2)成立，则mg(x2)恒成立，则mg(x2)成立，则mg(x2)恒成立，则mg(x2)max，即f(1)>g(2)，即e>ln 2+m>m，故①正确；‎ ‎②等价于在[1，2]上，f(x)min>g(x)min，即e>m，所以mg(x)max，即f(1)>g(2)，即e>ln 2+m，所以mg(x)min，即f(1)>g(1)，得e>m，④正确； ‎ ‎⑤等价于在[1，2]上，f(x)max>g(x)max，即f(2)>g(2)，得e2>ln 2+m>m，⑤正确， ‎ ‎【思维建模】 等价转化是数学解题中应用最为广泛的一种数学解题思想，也是一种解题方法，其核心内涵是把待解决的问题化为另外一个更为容易解决、或者我们更为熟悉的问题，等价转化后的问题可以使用综合法、数形结合法等方法加以解决，‎ ‎【变式探究】已知函数f(x)=(2-a)(x-1)-2ln ，g(x)=xe1-x(a∈R，e为自然对数的底数)，若对任意给定的x0∈(0，e]在(0，e]上总存在两个不同的xi(i=1，2)，使得f(xi)=g(x0)成立，则a的取值范围是(　　) ‎ ‎ (A)(-∞，] (B)(-∞，]‎ ‎(C)(，2) (D)[，)‎ 解题策略二　间接求解 根据客观题不要求过程、只要结果的特点，客观题也可以采用“非常规”的方法解决，主要有 特殊值法、逐项排除法、定性分析法等，‎ 方法1　特殊值验证法 ‎【例1】 已知y=f(x)与y=g(x)的图象如图中(1)(2)所示，则函数F(x)=f(x)·g(x)的图象可能是(　　) ‎ ‎ ‎ ‎【思维建模】 特殊点判断法 图象中的特殊点(如零点、极值点、与坐标轴交点等)常常有某种特定的含义，往往能为解题提供重要的信息， ‎ ‎【变式探究】(2017·全国Ⅲ卷)函数y=1+x+ 的部分图象大致为(　　)‎ ‎【解析】当x→+∞时，y=1+x+→+∞，排除B；当01，排除A，C，故选D。学* ‎ 方法2　逐项排除法 ‎ ‎【例2】(2017·全国Ⅰ卷)几位大学生响应国家的创业号召，开发了一款应用软件，为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动，这款软件的激活码为下面数学问题的【答案】已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下 的两项是20，21，再接下 的三项是20，21，22，依此类推，求满足如下条件的最小整数N N>100且该数列的前N项和为2的整数幂，那么该款软件的激活码是(　　)‎ ‎(A)440 (B)330 (C)220 (D)110‎ ‎【变式探究】如图，直三棱柱ABC-A1B1C1中，AA1=2，AB=BC=1，∠ABC=90°，外接球的球心为O，点E是侧棱BB1上的一个动点，有下列判断 ‎ ‎①直线AC与直线C1E是异面直线；②A1E一定不垂直AC1；③三棱锥E-AA1O的体积为定值；④AE+EC1的最小值为2 ，其中正确的个数是(　　)‎ ‎ ‎ ‎(A)1 (B)2 (C)3 (D)4‎ ‎【解析】①因为点A∉平面BB1C1C，所以直线AC与直线C1E是异面直线；②A1E⊥AB1时，直线A1E⊥平面AB1C1，此时A1E⊥AC1；③球心O是直线AC1，A1C的交点，底面OAA1面积不变，直线BB1∥平面AA1O，所以点E到底面距离不变，体积为定值；④将矩形AA1B1B和矩形BB1C1C展开到一个平面内，当点E为AC1与BB1交点时，AE+EC1取得最小值2 ，综上可知，正确的判断是①③④，故选C。 ‎ 方法3　定性分析法 ‎【例6】 (2016·全国Ⅰ卷)已知函数f(x)=sin(ωx+)(ω>0，||≤)，x=-为f(x)的零点，x=为y=f(x)图象的对称轴，且f(x)在（，）上单调，则ω的最大值为(　　)‎ ‎(A)11 (B)9 (C)7 (D)5 ‎ ‎【变式探究】已知函数f(x)=sin(2x+)(0<<)的图象的一个对称中心为（，0），则函数f(x)的单调递减区间是(　　)‎ ‎(A)[2 π-，2 π+]( ∈ )‎ ‎(B)[2 π+，2 π+]( ∈ )‎ ‎(C)[ π-， π+]( ∈ )‎ ‎(D)[ π+， π+] ( ∈ )‎ ‎【解析】函数f(x)的最小正周期为π，函数图象关于点(，0)中心对称，其单调区间(增或者减)的端点只能在左右各个单位，即单调增区间或者单调减区间有一个区间一定是[，]，结合正周期和选项，只能是选项D中的结论，故选D。 ‎