高考数学【理科】真题分类详细解析版专题16 直线和圆(原卷版)
专题16 直线和圆
【2013高考真题】
(2013·新课标Ⅱ理)(12)已知点A(-1,0);B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是
(A)(0,1) (B)(1-,) ( C)(1-, (D)[,)
(2013·新课标Ⅱ理)(9)已知a>0,x,y满足约束条件,若z=2x+y的最小值为1,则a=
(A) (B) (C)1 (D)2
(2013·新课标Ⅱ理)(4)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l ⊥m,l ⊥n,l则( )
(A)α∥β且∥α (B)α⊥β且⊥β
(C)α与β相交,且交线垂直于 (D)α与β相交,且交线平行于
(2013·浙江理)13、设,其中实数满足,若的最大值为12,则实数________。
(2013·天津理)11. 已知圆的极坐标方程为, 圆心为C, 点P的极坐标为, 则|CP| = .
(2013·天津理)4. 已知下列三个命题:
①若一个球的半径缩小到原来的, 则其体积缩小到原来的;
②若两组数据的平均数相等, 则它们的标准差也相等;
③直线x + y + 1 = 0与圆相切.
其中真命题的序号是: ( )
(A) ①②③ (B) ①②
(C) ①③ (D) ②③
(2013·天津理)2. 设变量x, y满足约束条件则目标函数z = y-2x的最小值为( )
(A) -7 (B) -4
(C) 1 (D) 2
(2013·陕西理)13. 若点(x, y)位于曲线与y=2所围成的封闭区域, 则2x-y的最小值为 .
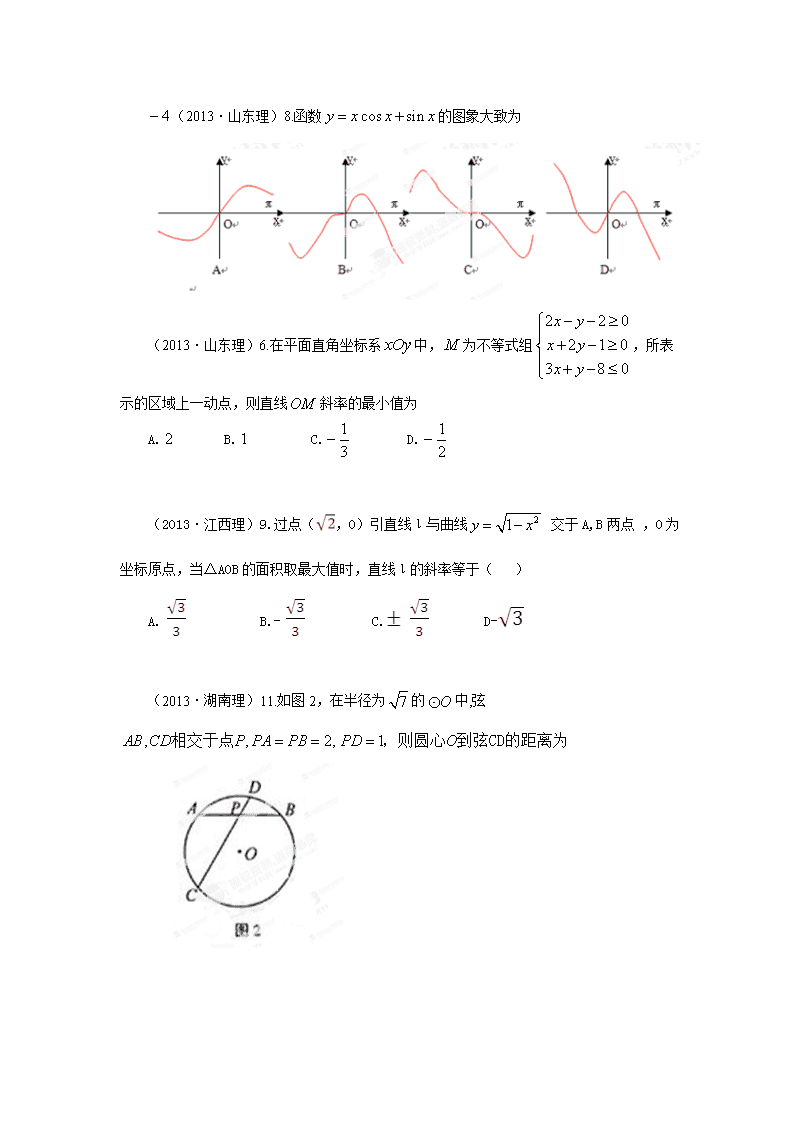
(2013·山东理)8.函数的图象大致为
(2013·山东理)6.在平面直角坐标系中,为不等式组,所表示的区域上一动点,则直线斜率的最小值为
A. B. C. D.
(2013·江西理)9.过点(,0)引直线ι与曲线 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
A. B.- C. D-
(2013·湖南理)11.如图2,在半径为的中,弦
(2013·湖南理)4.若变量满足约束条件,
A. B. C. D.
(2013·大纲理)15.记不等式组,所表示的平面区域为D.若直线与D有公共点,则a的取值范围是
(2013·广东理)13. 给定区域:,令点集
是在上取得最大值或最小值的点,则中的点共确定______
条不同的直线.
(2013·湖南理)9.在平面直角坐标系中,若
右顶点,则常数 .
(2013·大纲理)16.已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,,且圆O与圆K所在的平面所成的一个二面角为,则球O的表面积等于
(2013·北京理)11.如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D,PA=3,,则PD= ,AB= .
9.在极坐标系中,点(2,)到直线ρsinθ=2的距离等于
(2013·北京理)8.设关于x,y的不等式组表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,求得m的取值范围是
A. B. C. D.
(2013·安徽理)(7)在极坐标系中,圆的垂直于极轴的两条切线方程分别为
(A) (B)
(C) (D)
(2013·安徽理)(3)在下列命题中,不是公理的是( )
(A)平行于同一个平面的两个平面相互平行
(B)过不在同一条直线上的三点,有且只有一个平面
(C)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
(D)如果两个不重合的平面有一个公共点,
那么他们有且只有一条过该点的公共直线
(2013·安徽理)(18)(本小题满分12分)
设椭圆的焦点在轴上
(Ⅰ)若椭圆的焦距为1,求椭圆的方程;
(Ⅱ)设分别是椭圆的左、右焦点,为椭圆上第一象限内的点,直线交轴与点,并且,证明:当变化时,点在某定直线上。
(2013·安徽理)(19)(本小题满分13分)
如图,圆锥顶点为。底面圆心为,其母线与底面所成的角为。和
是底面圆上的两条平行的弦,轴与平面所成的角为,
(Ⅰ)证明:平面与平面的交线平行于底面;
(Ⅱ)求。
(2013·陕西理)20. (本小题满分13分)
已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(Ⅰ) 求动圆圆心的轨迹C的方程;
(Ⅱ) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P, Q, 若x轴是的角平分线, 证明直线l过定点.
(2013·上海理)22.(3分+5分+8分)如图,已知曲线,曲线,P是平面上一点,若存在过点P的直线与都有公共点,则称P为“C1—C2型点”.
(1)在正确证明的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线与有公共点,求证,进而证明原点不是“C1—C2型点”;
(3)求证:圆内的点都不是“C1—C2型点”.
(2013·天津理)13. 如图, △ABC为圆的内接三角形, BD为圆的弦, 且BD//AC. 过点
A 做圆的切线与DB的延长线交于点E, AD与BC交于点F. 若AB = AC, AE = 6, BD = 5, 则线段CF的长为 .
(2013·新课标Ⅱ理)(22)(本小题满分10分)选修4-1几何证明选讲
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,
且BCAE=DCAF,B、E、F、C四点共圆。
(Ⅰ)证明:CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值。
(2013·新课标Ⅱ理)(22)(本小题满分10分)选修4-1几何证明选讲
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,
且BCAE=DCAF,B、E、F、C四点共圆。
(Ⅰ)证明:CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值。
1.(2012·北京卷) 在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F,且与该抛物线相交于A,B两点,其中点A在x轴上方,若直线l的倾斜角为60°,则△OAF的面积为________.
2.(2012·浙江卷) 定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=________.
3.(2012·北京卷) 已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).
(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
4.(2012·陕西卷) 已知椭圆C1:+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,=2,求直线AB的方程.
5.(2012·上海卷) 若n=(-2,1)是直线l的一个法向量,则l的倾斜角的大小为________(结果用反三角函数值表示).
6.(2012·浙江卷) 设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
7.(2012·湖北卷) 设A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0,且m≠1).当点A在圆上运动时,记点M的轨迹为曲线C.
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标;
(2)过原点且斜率为k的直线交曲线C于P,Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H.是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
8.(2012·课标全国卷) 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若∠BFD=90°,△ABD的面积为4,求p的值及圆F的方程;
(2)若A、B、F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
9.(2012·广东卷) 在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的离心率e=,且椭圆C上的点到点Q(0,2)的距离的最大值为3.
(1)求椭圆C的方程;
(2)在椭圆C上,是否存在点M(m,n),使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A、B,且△OAB的面积最大?若存在,求出点M的坐标及对应的△OAB
的面积;若不存在,请说明理由.
10.(2012·江苏卷) 在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
11.(2012·陕西卷) 已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则( )
A.l与C相交
B.l与C相切
C.l与C相离
D.以上三个选项均有可能
12.(2012·重庆卷) 对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系一定是( )
A.相离 B.相切
C.相交但直线不过圆心 D.相交且直线过圆心
13.(2012·天津卷) 设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A.[1-,1+]
B.(-∞,1-]∪[1+,+∞)
C.[2-2,2+2]
D.(-∞,2-2]∪[2+2,+∞)
14.(2012·重庆卷) 设平面点集A=(x,y)(y-x)·y-≥0,B=,则A∩B所表示的平面图形的面积为( )
A.π B.π
C.π D.
【答案】D 【解析】平面点集A表示的平面区域就是不等式组与
15.(2012·课标全国卷)设F1,F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
A. B. C. D.
【答案】C 【解析】根据题意,一定有∠PF1F2=30°,且∠PF2x=60°,故直线PF2的倾斜角是,设直线x=a与x轴的交点为M,则|PF2|=2|F2M|,又|PF2|=|F1F2|,所以|F1F2|=2|F2M|.所以2c=2,即4c=3a,故e==.故选C.
16.(2012·天津卷)设椭圆+=1(a>b>0)的左、右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为-,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|>.
【答案】解:(1)设点P的坐标为(x0,y0).
由题意,有+=1. ①
由A(-a,0),B(a,0),得kAP=,kBP=.
由kAP·kBP=-,可得x=a2-2y,代入①并整理得(a2-2b2)y=0.由于y0≠0,故a2=2b2.于是e2==,所以椭圆的离心率e=.
(2)证明:(方法一)
依题意,直线OP的方程为y=kx,
设点P的坐标为(x0,y0).
由条件得消去y0并整理得
17.(2012·陕西卷)已知椭圆C1:+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,=2,求直线AB的方程.
【答案】解:(1)由已知可设椭圆C2的方程为+=1(a>2),
其离心率为,故=,则a=4,故椭圆C2的方程为+=1.
(2)解法一:A,B两点的坐标分别记为(xA,yA),(xB,yB),
由=2及(1)知,O,A,B三点共线且点A,B不在y轴上,
因此可设直线AB的方程为y=kx.
将y=kx代入+y2=1中,得(1+4k2)x2=4,
所以x=,
18.(2012·重庆卷)如图1-3,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.
图1-3
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线l交椭圆于P,Q两点,使PB2⊥QB2,求直线l的方程.
【答案】解:(1)设所求椭圆的标准方程为+=1(a>b>0),右焦点为F2(c,0).
因△AB1B2是直角三角形,又|AB1|=|AB2|,故∠B1AB2为直角,因此|OA|=|OB2|,得b=.结合c2=a2-b2得4b2=a2-b2,故a2=5b2,c2=4b2,所以离心率e==.
在Rt△AB1B2中,OA⊥B1B2,故
S△AB1B2=·|B1B2|·|OA|=|OB2|·|OA|=·b=b2.
由题设条件S△AB1B2=4,得b2=4,从而a2=5b2=20.
因此所求椭圆的标准方程为:
+=1.
(2)由(1)知B1(-2,0),B2(2,0).由题意知直线l的倾斜角不为0,故可设直线l的方程为:
x=my-2.代入椭圆方程得(m2+5)y2-4my-16=0.
设P(x1,y1)、Q(x2,y2),则y1,y2是上面方程的两根,因此
y1+y2=,y1·y2=-,
又=(x1-2,y1),=(x2-2,y2),所以
·=(x1-2)(x2-2)+y1y2
=(my1-4)(my2-4)+y1y2
=(m2+1)y1y2-4m(y1+y2)+16
=--+16
=-,
由PB2⊥QB2,得·=0,即16m2-64=0,解得m=±2.
所以满足条件的直线有两条,其方程分别为x+2y+2=0和x-2y+2=0.
19.(2012·辽宁卷)如图1-7,椭圆C0:+=1(a>b>0,a,b为常数),动圆C1:x2+y2=t,b<t1<a.点A1,A2分别为C0的左,右顶点.C1与C0相交于A,B,C,D四点.
图1-7
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=t与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等.证明:t+t为定值.
【答案】解:(1)设A(x1,y1),B(x1,-y1),又知A1(-a,0),A2(a,0),则
直线A1A的方程为y=(x+a),①
直线A2B的方程为y=(x-a),②
19.(2012·北京卷) 已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).
(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
【答案】解:(1)曲线C是焦点在x轴上的椭圆,当且仅当
解得
0,
即k2>.
设点M,N的坐标分别为(x1,y1),(x2,y2),则
y1=kx1+4,y2=kx2+4,
x1+x2=,x1x2=.
直线BM的方程为y+2=x,点G的坐标为.
因为直线AN和直线AG的斜率分别为kAN=,kAG=-,
所以kAN-kAG=+
=+
=k+
=k+=0,
即kAN=kAG.故A,G,N三点共线.
20.(2012·广东卷)在平面直角坐标系xOy中,已知椭圆C:+=1(a>b>0)的离心率e=,且椭圆C上的点到点Q(0,2)的距离的最大值为3.
(1)求椭圆C的方程;
(2)在椭圆C上,是否存在点M(m,n),使得直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A、B,且△OAB的面积最大?若存在,求出点M的坐标及对应的△OAB的面积;若不存在,请说明理由.
【答案】解:(1)∵e===,
假设直线l:mx+ny=1与圆O:x2+y2=1相交于不同的两点A、B,则圆心O到l的距离
d=<1.
因为点M(m,n)∈C,所以+n2=1b>0)的左、右焦点,过点F1作x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2的垂线交直线x=于点Q.
(1)如果点Q的坐标是(4,4),求此时椭圆C的方程;
(2)证明:直线PQ与椭圆C只有一个交点.
【答案】解:(1)(方法一)由条件知,P,
故直线PF2的斜率为kPF2==-.
因为PF2⊥F2Q,所以直线F2Q的方程为y=x-,故Q.
由题设知,=4,2a=4,解得a=2,c=1.
故椭圆方程为+=1.
(方法二)设直线x=与x轴交于点M,
由条件知,P.
因为△PF1F2∽△F2MQ,所以=.
即=,解得=2a.
所以a=2,c=1,
故椭圆方程为+=1.
(2)证明:直线PQ的方程为=,
即y=x+a.
将上式代入椭圆方程得,x2+2cx+c2=0.
解得x=-c,y=,
所以直线PQ与椭圆C只有一个交点.
22.(2012·福建卷)如图1-4,椭圆E:+=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=,过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
图1-4
(2)由得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)
此时x0=-=-,y0=kx0+m=,所以P.
由得Q(4,4k+m).
解法二:(1)同解法一.
(2)由得(4k2+3)x2+8kmx+4m2-12=0.
因为动直线l与椭圆E有且只有一个公共点P(x0,y0),所以m≠0且Δ=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0.(*)
此时x0=-=-,y0=kx0+m=,所以P.
由得Q(4,4k+m).
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.
取k=0,m=,此时P(0,),Q(4,),以PQ为直径的圆为(x-2)2+(y-)2=4,交x轴于点M1(1,0),M2(3,0);取k=-,m=2,此时P,Q(4,0),以PQ为直23.(2012·湖北卷)设A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0,且m≠1).当点A在圆上运动时,记点M的轨迹为曲线C.
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标;
(2)过原点且斜率为k的直线交曲线C于P,Q两点,其中P在第一象限,它在y
轴上的射影为点N,直线QN交曲线C于另一点H.是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
N(0,kx1),直线QN的方程为y=2kx+kx1,将其代入椭圆C的方程并整理可得(m2+4k2)x2+4k2x1x+k2x-m2=0.
依题意可知此方程的两根为-x1,x2,于是由韦达定理可得
-x1+x2=-,即x2=.
因为点H在直线QN上,
所以y2-kx1=2kx2=.
于是=(-2x1,-2kx1),
=(x2-x1,y2-kx1)=.
而PQ⊥PH等价于·==0,
即2-m2=0,又m>0,得m=,
故存在m=,使得在其对应的椭圆x2+=1上,对任意的k>0,都有PQ⊥PH.
方法2:如图(2)、(3),对任意x1∈(0,1),设P(x1,y1),H(x2,y2),则Q(-x1,-y1),N(0,y1).
因为P,H两点在椭圆C上,所以
两式相减可得
m2(x-x)+(y-y)=0.③
依题意,由点P在第一象限可知,点H也在第一象限,且P,H不重合,
故(x1-x2)(x1+x2)≠0.于是由③式可得
=-m2.④
又Q,N,H三点共线,所以kQN=kQH,即=.
于是由④式可得kPQ·kPH=·=·=-.
而PQ⊥PH等价于kPQ·kPH=-1,即-=-1,又m>0,得m=,
故存在m=,使得在其对应的椭圆x2+=1上,对任意的k>0,都有PQ⊥PH.
24.(2012·江西卷)椭圆+=1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2,若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.
25.(2012·山东卷)已知椭圆C:+=1(a>b>0)的离心率为.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
A.+=1 B.+=1
C.+=1 D.+=1
【答案】D 【解析】本题考查椭圆的方程及直线与椭圆的位置关系,考查运算求解能力,中档题.
由离心率为得,a2=4b2,排除选项B,双曲线的渐近线方程为y=±x,与椭圆的四交点组成的四边形的面积为16可得在第一象限的交点坐标为,代入选项A、C、D,知选项D正确.
26.(2012·上海卷)在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值.
【答案】解:(1)双曲线C1:-y2=1,左顶点A,渐近线方程:y=±x.
过点A与渐近线y=x平行的直线方程为y=,即y=x+1.
解方程组得
所以所求三角形的面积为S=|OA||y|=.
(2)设直线PQ的方程是y=x+b,因直线PQ与已知圆相切,
故=1,即b2=2.
由得x2-2bx-b2-1=0.
设P(x1,y1)、Q(x2,y2),则
又y1y2=(x1+b)(x2+b),所以
·=x1x2+y1y2=2x1x2+b(x1+x2)+b2
=2(-1-b2)+2b2+b2=b2-2=0.
故OP⊥OQ.
(3)当直线ON垂直于x轴时,
|ON|=1,|OM|=,则O到直线MN的距离为.
当直线ON不垂直于x轴时,
设直线ON的方程为y=kx,
则直线OM的方程为y=-x.
由得所以|ON|2=.
27.(2012·四川卷)椭圆+=1的左焦点为F,直线x=m与椭圆相交于点A、B.当△FAB的周长最大时,△FAB的面积是________.
【答案】3 【解析】如图,设椭圆右焦点为F′,直线x=m与x轴相交于C,
由椭圆第一定义,|AF|+|AF′|=|BF|+|BF′|=2a=4,
而|AB|=|AC|+|BC|≤|AF′|+|BF′|,
∴当且仅当AB过F′时,△ABF周长最大.
此时,由c=1,得A,B,即|AB|=3,
∴S△ABF=|AB||FF′|=3.
【2011高考真题】
(2011·安徽卷)在平面直角坐标系中,如果x与y都是整数,就称点(x,y)为整点,下列命题中正确的是________(写出所有正确命题的编号).
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果k与b都是无理数,则直线y=kx+b不经过任何整点;
③直线l经过无穷多个整点,当且仅当l经过两个不同的整点;
④直线y=kx+b经过无穷多个整点的充分必要条件是:k与b都是有理数;
⑤存在恰经过一个整点的直线.
【答案】①③⑤
【解析】 ①正确,比如直线y=x+,不与坐标轴平行,且当x取整数时,y始终是一个无理数,即不经过任何整点;②错,直线y=x-中k与b都是无理数,但直线经过整点(1,0);③正确,当直线经过两个整点时,它经过无数多个整点;④错误,当k=0,b=时,直线y=不通过任何整点;⑤正确,比如直线y=x-只经过一个整点(1,0).
(2011·福建卷)已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,求该圆的方程;
(2)若直线l关于x轴对称的直线为l′,问直线l′与抛物线C:x2=4y是否相切?说明理由.
【解答】 解法一:
图1-6
(1)依题意,点P的坐标为(0,m).
因为MP⊥l,所以×1=-1,
解得m=2,即点P的坐标为(0,2).
从而圆的半径
r=|MP|==2,
故所求圆的方程为(x-2)2+y2=8.
(2)因为直线l的方程为y=x+m,
所以直线l′的方程为y=-x-m.
由得x2+4x+4m=0.
Δ=42-4×4m=16(1-m).
①当m=1,即Δ=0时,直线l′与抛物线C相切;
②当m≠1,即Δ≠0时,直线l′与抛物线C不相切.
综上,当m=1时,直线l′与抛物线C相切;当m≠1时,直线l′与抛物线C不相切.
解法二:
(1)设所求圆的半径为r,则圆的方程可设为(x-2)2+y2=r2.
依题意,所求圆与直线l:x-y+m=0相切于点P(0,m),则
解得
所以所求圆的方程为(x-2)2+y2=8.
(2)同解法一.
图1-2
(2011·湖北卷)如图1-2,直角坐标系xOy所在的平面为α,直角坐标系x′Oy′(其中y′轴与y轴重合)所在的平面为β,∠xOx′=45°.
(1)已知平面β内有一点P′(2,2),则点P′在平面α内的射影P的坐标为________;
(2)已知平面β内的曲线C′的方程是(x′-)2+2y′2-2=0,则曲线C′在平面α内的射影C的方程是______________.
2+y2=1.
(2011·福建卷)设圆锥曲线Γ的两个焦点分别为F1,F2.若曲线Γ上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线Γ的离心率等于( )
A.或 B.或2
C.或2 D.或
【答案】A
【解析】 设|F1F2|=2c(c>0),由已知|PF1|∶|F1F2|∶|PF2|=4∶3∶2,得|PF1|=c,|PF2|=c,且|PF1|>|PF2|,
若圆锥曲线Γ为椭圆,则2a=|PF1|+|PF2|=4c,离心率e==;
若圆锥曲线Γ为双曲线,则2a=|PF1|-|PF2|=c,离心率e==,故选A.
(2011·湖南卷)如图1-9,椭圆C1:+=1(a>b>0)的离心率为,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
(1)求C1,C2的方程;
(2)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
①证明:MD⊥ME;
②记△MAB,△MDE的面积分别为S1,S2.问:是否存在直线l,使得=?请说明理由.
图1-10
【解答】 (1)由题意知,e==,从而a=2b.又2=a,解得a=2,b=1.
故C1,C2的方程分别为+y2=1,y=x2-1.
(2)①由题意知,直线l的斜率存在,设为k,则直线l的方程为y=kx.
由得x2-kx-1=0.
设A(x1,y1),B(x2,y2),
则x1,x2是上述方程的两个实根,
于是x1+x2=k,x1x2=-1.
又点M的坐标为(0,-1),所以
y=k1x-1,由解得
或
则点A的坐标为(k1,k-1).
又直线MB的斜率为-,同理可得点B的坐标为.
于是S1=|MA|·|MB|=·|k1|··=.
由得(1+4k)x2-8k1x=0.
解得或
则点D的坐标为.
又直线ME的斜率为-,同理可得点E的坐标为.
于是S2=|MD|·|ME|=.
(2011·江西卷)若椭圆+=1的焦点在x轴上,过点作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.
【答案】 +=1
【解析】 由题可知过点与圆x2+y2=1的圆心的直线方程为y=x,由垂径定理可得kAB=-2.
显然过点的一条切线为直线x=1,此时切点记为A(1,0),即为椭圆的右焦点,故c=1.
由点斜式可得,直线AB的方程为y=-2(x-1),
即AB:2x+y-2=0.
令x=0得上顶点为(0,2),∴b=2,∴a2=b2+c2=5,故得所求椭圆方程为+=1.
(2011·课标全国卷)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2
在x轴上,离心率为.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________________.
【答案】 +=1
【解析】 设椭圆方程为+=1(a>b>0).
因为离心率为,所以=,
解得=,即a2=2b2.
图1-7
又△ABF2的周长为++=+++=(+)+(+)=2a+2a=4a,,所以4a=16,a=4,所以b=2,
所以椭圆方程为+=1.
(2011·陕西卷)
图1-8
如图1-8,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=|PD|.
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为的直线被C所截线段的长度.
将直线方程y=(x-3)代入C的方程,得
+=1,即x2-3x-8=0.
∴x1=,x2=.
∴线段AB的长度为
|AB|====.
(2011·浙江卷)设F1,F2分别为椭圆+y2=1的左,右焦点,点A,B在椭圆上.若=5,则点A的坐标是________.
【答案】(0,±1)
【解析】 设直线F1A的反向延长线与椭圆交于点B′,又∵=5,由椭圆的对称性可得=5,设A,B′,
又∵|F1A|=,|F1B′|=,
∴ 解之得x1=0,
∴点A的坐标为.
(2011·安徽卷)双曲线2x2-y2=8的实轴长是( )
A.2 B.2 C.4 D.4
【答案】C
【解析】 双曲线方程可化为-=1,所以a2=4,得a=2,所以2a=4.故实轴长为4.
(2011·全国卷)已知F1、F2分别为双曲线C:-=1的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2的平分线,则|AF2|=________.
【答案】6
【解析】 根据角平分线的性质,==.又-=6,故=6.
【2010高考真题】
1.(2010江西理)8.直线与圆相交于M,N两点,若,则k的取值范围是
A. B. C. D.
2.(2010重庆理)(8) 直线y=与圆心为D的圆交与A、B两点,则直线AD与BD的倾斜角之和为
A. B. C. D.
【答案】C
【解析】数形结合
由圆的性质可知
故
3.(2010安徽理)9、动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间时,点的坐标是,则当时,动点的纵坐标关于(单位:秒)的函数的单调递增区间是
A、 B、 C、 D、和
【答案】 D
【解析】画出图形,设动点A与轴正方向夹角为,则时,每秒钟旋转,在上,在上,动点的纵坐标关于都是单调递增的。
4.(2010四川理)(14)直线与圆相交于A、B两点,则 .
解析:方法一、圆心为(0,0),半径为2
圆心到直线的距离为d=
故
得|AB|=2
答案:2
5.(2010广东理)12.已知圆心在x轴上,半径为的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
答案:.
解析:设圆心为,则,解得
【2009高考真题】
1.(辽宁理,4)已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为
A. B.
C. D.
【解析】圆心在x+y=0上,排除C、D,再结合图象,或者验证A、B中圆心到两直线的距离等于半径即可.
【答案】B
2.(重庆理,1)直线与圆的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
【解析】圆心为到直线,即的距离,而,选B。
【答案】B
3.(天津理,13)设直线的参数方程为(t为参数),直线的方程为
y=3x+4则与的距离为_______
【解析】由题直线的普通方程为,故它与与的距离为。
【答案】
4.(全国Ⅱ理16)已知为圆:的两条相互垂直的弦,垂足为,则四边形的面积的最大值为 。
【解析】设圆心到的距离分别为,则.
四边形的面积
【答案】5
6.(2009江苏卷18)(本小题满分16分)
在平面直角坐标系中,已知圆和圆.
(1)若直线过点,且被圆截得的弦长为,求直线的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线和,它们分别与圆和圆相交,且直线被圆截得的弦长与直线被圆截得的弦长相等,试求所有满足条件的点P的坐标。
【解析】
解:(1)设直线的方程为:,即
由垂径定理,得:圆心到直线的距离,
结合点到直线距离公式,得:
化简得:
求直线的方程为:或,即或
(2) 设点P坐标为,直线、的方程分别为:
,即:
因为直线被圆截得的弦长与直线被圆截得的弦长相等,两圆半径相等。
由垂径定理,得::圆心到直线与直线的距离相等。
故有:,
化简得:
关于的方程有无穷多解,有:
解之得:点P坐标为或。
【2008年高考真题】
1.(2008年全国Ⅱ理11)等腰三角形两腰所在直线的方程分别为与x-7y-4=0,
原点在等腰三角形的底边上,则底边所在直线的斜率为 ( ).
A.3 B.2 C. D.
答案 A
解析 ,,设底边为
由题意,到所成的角等于到所成的角于是有
再将A、B、C、D代入验证得正确答案 是A。
2.(2008·江苏18)在平面直角坐标系中,二次函数()与两坐标轴有三个交点.记过三个交点的圆为圆.
(Ⅰ)求实数b的取值范围;
(Ⅱ)求圆的方程;
(Ⅲ)圆是否经过定点(与的取值无关)?证明你的结论.