- 2021-07-01 发布 |
- 37.5 KB |
- 17页

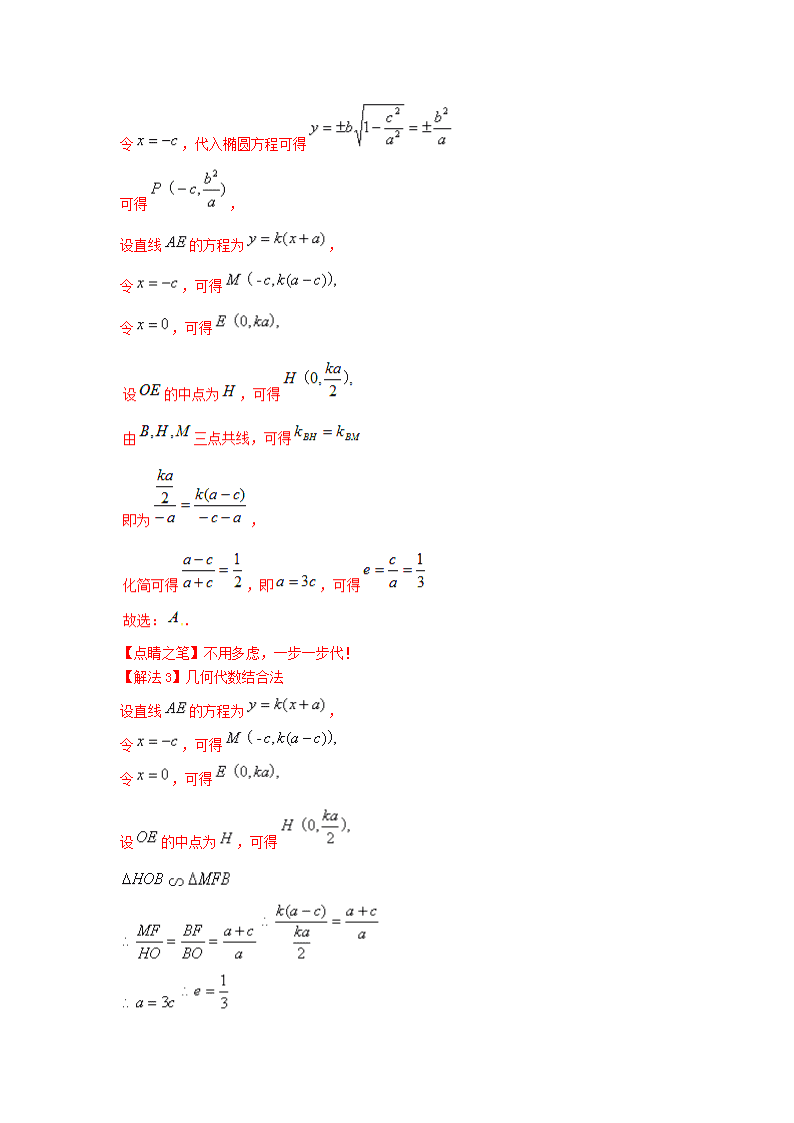

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习北师大版一题多解,玩透椭圆离心率学案
一、典例分析,融合贯通 典例 1 【2016 年高考数 新课标Ⅲ卷文 12 题】已知O 为坐标原点, F 是椭圆C )0(12 2 2 2 ba b y a x 的左焦点, BA, 分别为C 的左,右顶点.P 为上C 一点,且 xPF 轴,过点 A 的直线l 与线段 PF 交于点 M 与 y 轴交于点 E .若直线 BM 经过 OE 的中点, 则C 的离心率为( ) A . 3 1 B . 2 1 C . 3 2 D. 4 3 【点睛之笔】相似用完即相识! 【解法 2】代数法 由题意可设 )0,( cF , )0,( aA , )0,(aB 令 cx ,代入椭圆方程可得 a b a cby 2 2 2 1 可得 ), 2 a bcP ( , 设直线 AE 的方程为 )( axky , 令 cx ,可得 ,)(,- )( cakcM ] 令 0x ,可得 ,,0 )( kaE 【点睛之笔】不用多虑,一步一步代! 【解法 3】几何代数结合法 设直线 AE 的方程为 )( axky , 令 cx ,可得 ,)(,- )( cakcM [ 令 0x ,可得 ,,0 )( kaE 设OE 的中点为 H ,可得 ,2,0 )( kaH HOB ∽ MFB a ca BO BF HO MF a ca ka cak 2 )( ca 3 3 1e 【点睛之笔】几何代数,数与形的完美融合! 【解后反思】 解法 1 利用相似比构造方程,恒等变形求得离心率![ ] 解法 2 利用条件一步一步用数据转化,无须烧脑! 解法 3 几何代数,相辅相生,相得益彰! 典例 2 设 P 是 2 2 1 02 2 x y a b a b 上的一点, 1F 、 2F 是其左、右焦点 .已知 1 2F PF =60 ,求椭圆离心率的取值范围. 【解法 1】基本不等式 在 1 2F PF 中, 2 2 2 1 2 1 2 1 2PF + PF -2 PF PF cos60 FF , 22 1 2 1 2 1 2( PF + PF ) -3 PF PF FF 2 2 1 22 1 2 1 2 1 2 3( PF + PF )3 PF PF ( PF + PF ) - FF 4 2 2 2 23 44 4 34 aa c a 2 24a c 2 1 4e 0 1e 又 1 12 e 【点睛之笔】基本不等式,让数 习更有激情! 【解法 2】有界性 设 0 0P x ,y , 1 0 2 0PF , PFa ex a ex ,又 1 2FF 2c 在 1 2F PF 中, 2 2 2 1 2 1 2 1 2PF + PF -2 PF PF cos60 FF , 2 2 2 0 0 0 0+ -2 cos60 4a ex a ex a ex a ex c , 【点睛之笔】坐标有界,思想无界! 【解法 3】极端情况 当点 P 位于短轴端点 1B 或 2B 处时,点 P 对两焦点的张角最大 故 1 2 2 1 2FB F FPF =60 , 2 2OB F 30 (O 为坐标原点) 在 2 2OB F 中, 2 2 1sin OB F sin30 2 ce a , 0 1e 又 1 12 e 【点睛之笔】极端解法,剑走偏锋! 【解后反思】 解法 1 套用公式省时又省力![ X X ] 解法 2 利用坐标的有界性巧妙构造不等式! 解法 3 极端解法,投“极”取巧,尽显思维的灵气! 典例 3【2016 浙江理第 19 题】如图,设椭圆 2 2 2 1( 1)x y aa (Ⅰ)求直线 1 kxy 被椭圆截得的线段长(用 ka, 表示); (Ⅱ)若任意以 )1,0(A 为圆心的圆与椭圆至多有三个公共点,求椭圆离心率的取值范围。 第(1)小题 第(2)小题 【解法 1】 零点存在定理 设圆方程为 222 1 ryx ,与椭圆联立方程 2222 222 )1( ayax ryx 消去 x 得 012)1( 2222 aryya 由题设知方程在 1,1 上最多一解, 记 2 2 2 2( ) ( 1) 2 1f y a y y r a ① 当 42 r 时, 0)1( 2 rf , 2( 1) 4 0f r (1)f ( 1) 0f ,所以方程在 1,1 上只有一解, 1a 均可 ② 那么当 42 r 时, 第一种情况 只需 0)1)(1(44 222 ara ,得 02224 rraa 解得 2 4 2 4 22242 2 rrrrrra ,即 22 042 a ,得 2a 第二种情况 假设方程在 1,1 上有两解[ 。 。 ] 2 ( 1) 0 (1) 0 0 11 11 f f a ,得 11 04 0 2 2 2 a r r ,则 22 a , 由于方程在 1,1 上最多一解,所以 22 a 上述两种情况均可得到1 2a ,离心率 2 2 2 1 1 21 2 c ae a a a , 因此椭圆离心率的取值范围 20 2e 【点睛之笔】零点存在定理,走遍天下都有理! 【点睛之笔】方程法,缩短思维旅程的好方法! 【解法 3】点差法 因此,任意以 (0,1)A 为圆心的圆与椭圆至多有三个公共点的充要条件是 21 2a , 离心率 2 2 1c ae a a ,因此椭圆离心率的取值范围 20 2e 【点睛之笔】点差法,一点都不差的好方法! 【解法 4】单调性法 易知,弦长 PA 从 A 到 B 逆时针旋转半圈处处不相等,即弦长在 y 轴单侧单调。 | |PA 4 2 2 4 4 2 2 2 2 2 2 2 4 2 2 2 4 4(1 ) 2 21 2 1(1 ) ( ) a k k k k kk a k k k ka a a , 设 2k t , 2 2 2 4 ( ) 2 1 2 1 t tg t tk a a ,则 ( )g t 在 (0, )t 上单调递增。 只需 42 22 12 atattt ,即 42 12 atat 成立 得 2 2 1a ,得 22 a ,因此椭圆离心率的取值范围 2 20 e 【点睛之笔】单调性法,解起题 不单调! 【解法 5】 弦长的最值性 【点睛之笔】利用弦长的最值性,最有价值! 【解后反思】 解法 1 零点存在定理,剪不断那就理 乱! 解法 2 利用方程思想构造不等式,妙哉! 解法 3 点差法,代点作差,肯定不会差! 解法 4 单调性法,其实很有情调,一点都不不单调! 解法 5 利用最值性,直奔目标,不走寻常路! 二、精选试题,能力升级 1.【2012 全国,理 4】设 F1,F2 是椭圆 E 2 2 2 2 1x y a b (a>b>0)的左、右焦点,P 为直线 3 2 ax 上一点,△F2PF1 是底角为 30°的等腰三角形,则 E 的离心率为( ) A. 1 2 B. 2 3 C. 3 4 D. 4 5 【答案】C 【解析】设直线 3 2 ax 与 x 轴交于点 M ,则 2 60PF M = ,在 2Rt PF M 中, 2 1 2 2PF F F c= = , 2 3 2 aF M c ,故 2 2 3 12cos60 2 2 a cF M PF c ,解得 3 4 c a ,故离 心率 3 4e . 2.【2011 全国新课标,理 14】在平面直角坐标系 xOy 中,椭圆 C 的中心为原点,焦点 F1, F2 在 x 轴上,离心率为 2 2 .过 F1 的直线 l 交 C 于 A,B 两点,且△ABF2 的周长为 16,那么 C 的方程为__________. 【答案】 2 2 116 8 x y 【解析】 3.【2008 全国 1,理 15】在 ABC△ 中, AB BC , 7cos 18B .若以 A B, 为焦点的 椭圆经过点C ,则该椭圆的离心率 e . 【答案】 3 8 . 【解析】设 1AB BC , 7cos 18B 则 2 2 2 252 cos 9AC AB BC AB BC B 5 3AC , 5 8 2 32 1 ,2 1,3 3 2 8 ca c e a . 4.【2018 浙江温州一模】正方形 的四个顶点都在椭圆 上,若椭圆的焦点在 正方形的内部,则椭圆的离心率的取值范围是( ) A. B. C. D. 【答案】B 5.【2018 广西柳州市一模】已知点 P 是以 1 2,F F 为焦点的椭圆 2 2 2 2 1 0x y a ba b 上 一点,若 1 2 2 1, 2PF PF PF F ,则椭圆的离心率 e ( ) A. 5 3 B. 1 3 C. 2 3 D. 1 2 【答案】A 【解析】 点 P 是以 1 2F F, 为焦点的椭圆 2 2 2 2 1 0x y a ba b 上一点, 1 2 2 1 2PF PF tan PF F , , 1 2 PF PF 2 ,设 2PF x ,则 1 2PF x ,由椭圆定义知 2 2x x a , x 2 3 a , 2PF 2 3 a ,则 1PF 4 3 a ,由勾股定理知 2 2 2 2 1 1 2PF PF F F , 解得 5 3c a , 5 3 ce a . 6.【2018 广西三校九月联考】已知椭圆方程C 为 2 2 2 2 1x y a b , ( 0)a b 椭圆的右焦 点为 1,0 ,离心率为 1 2e ,直线l y kx m 与椭圆C 相交于 A 、 B 两点,且 3 4OA OBk k (1)椭圆的方程及求 AOB 的面积; (2)在椭圆上是否存在一点 P ,使OAPB 为平行四边形,若存在,求出 OP 的取值范围, 若不存在说明理由. 【答案】(1) 2 2 14 3 x y , S 3 (2)不存在 P 【解析】[ 。 。 ] 消去 y 化简得, 2 2 23 4 8 4 12 0k x kmx m , 1 2 2 8 3 4 kmx x k 2 1 2 2 4 12 3 4 mx x k , 0 得 2 24 3 0k m 2 1 2 1 2 1 2 1 2y y kx m kx m k x x km x x m , 2 2 2 2 2 2 2 2 4 12 8 3 12 3 4 3 4 3 4 m km m kk km mk k k . 3 4OA OBK K , 1 2 1 2 3 4 y y x x ,即 1 2 1 2 3 4y y x x 2 2 2 2 2 3 12 3 4 12 3 4 4 3 4 m k m k k 即 2 22 4 3m k , 2 2 22 2 1 2 1 2 22 48 4 3 AB 1 4 1 3 4 k m k x x x x k k = 2 22 2 22 48 1 24 13 4 2 3 43 4 k kk kk . O 到直线 y kx m 的距离 2 d 1 m k 2 22 2 2 22 24 1 24 11 1 1 2 2 3 4 2 1 3 41AOB k km mS d AB k k kk , 2 2 1 3 4 24 32 2 3 4 k k . (2)若存在平行四边形 OAPB 使 P 在椭圆上,则OP OA OB ,设 0 0P x y, , 则 0 1 2 2 8 3 4 kmx x x k , 0 1 2 2 6 3 4 my y y k ,由于 P 在椭圆上,所以 2 2 0 0 14 3 x y , 从而化简得 2 2 2 2 22 2 16 12 1 3 4 3 4 k m m k k 化简得 2 24 3 4m k ①, 由 3 4OA OBK K ,知 2 22 4 3m k ② 联立方程①②知 0m ,故不存在 P 在椭圆上的平行四边形. 7.【2018 河南中原名校质检二】已知椭圆 的离心率为 ,以原点为圆 心,椭圆的短半轴为半径的圆与直线 相切. (1)求椭圆 的方程 (2)设 , 是椭圆 上关于 轴对称的任意两个不同的点,连结 交椭圆 于另一点 , 证明直线 与 轴相交于定点 . 【答案】(1) (2) 8.【2018 吉林百校联盟九月联考】已知椭圆C 2 2 2 2 1( 0)x y a ba b 的离心率为 1 2 ,且 过点 2 3, 3 , A , B 是椭圆C 上异于长轴端点的两点. (1)求椭圆C 的方程; (2)已知直线l 8x ,且 1AA l ,垂足为 1A , 1BB l ,垂足为 1B ,若 3,0D ,且 1 1A B D 的面积是 ABD 面积的 5 倍,求 ABD 面积的最大值. 设 1 1,A x y , 2 2,B x y , AB 的直线方程为 2x my , 由 2 2 2,{ 3 4 48, x my x y 即 2 23 4 12 36 0m y my , 1 2 2 12 3 4 my y m , 1 2 2 36 3 4y y m , 2 1 2 1 2 1 2 1 1 42 2ABDS y y y y y y 2 22 112 3 4 m m 2 2 112 3 1 1 m m , 令 2 1 1t m ,所以 2 12 12 13 1 3 ABD tS t t t , 因为 1 1 33 3t tt t ,所以 13t t 在 1,3 上单调递增,所以在 1,t 上单调递 增, 所以 13 4t t ,所以 3ABDS (当且仅当 2 1 1t m ,即 0m 时“ ”成立), 故 ABDS 的最大值为3 . 9.【2014 课标Ⅰ,理 20】已知点 A (0,2) ,椭圆 E 2 2 2 2 1( 0)x y a ba b 的离心率为 3 2 ; F 是椭圆 E 的右焦点,直线 AF 的斜率为 2 3 3 ,O 为坐标原点 (I)求 E 的方程; (II)设过点 A 的动直线 l 与 E 相交于 P,Q 两点。当 OPQ 的面积最大时,求 l 的直线方程. 10.【2018 广西柳州市一模】已知椭圆 2 2 2 2: 1 0x yC a ba b 的离心率为 2 2 , 1 2F F、 为椭圆的左右焦点, P 为椭圆短轴的端点, 1 2PF F 的面积为 2. (1)求椭圆C 的方程; (2)设O 为原点,若点 A 在椭圆C 上,点 B 在直线 2y 上,且OA OB ,试判断直线 AB 与圆 2 2 2x y 的位置关系,并证明你的结论. 圆心O 到直线 AB 的距离 2d . 此时直线 AB 与圆 2 2 2x y 相切. 当 0x t 时,直线 AB 的方程为 0 0 22 yy x tx t . 即 0 0 0 02 2 0y x x t y x ty . 0 0 2 2 0 0 2 2 x tyd y x t 又 2 2 0 0 0 0 22 4, yx y t x ,故 2 2 0 0 0 0 0 2 4 2 2 2 0 0 0 0 0 2 2 0 0 2 42 2 4 8 164 2 y xx x xd y x xx y x x . 此时直线 AB 与圆 2 2 2x y 相切.查看更多