【数学】2018届一轮复习人教A版12-1合情推理与演绎推理学案

【数学】2018届一轮复习人教A版12-1合情推理与演绎推理学案

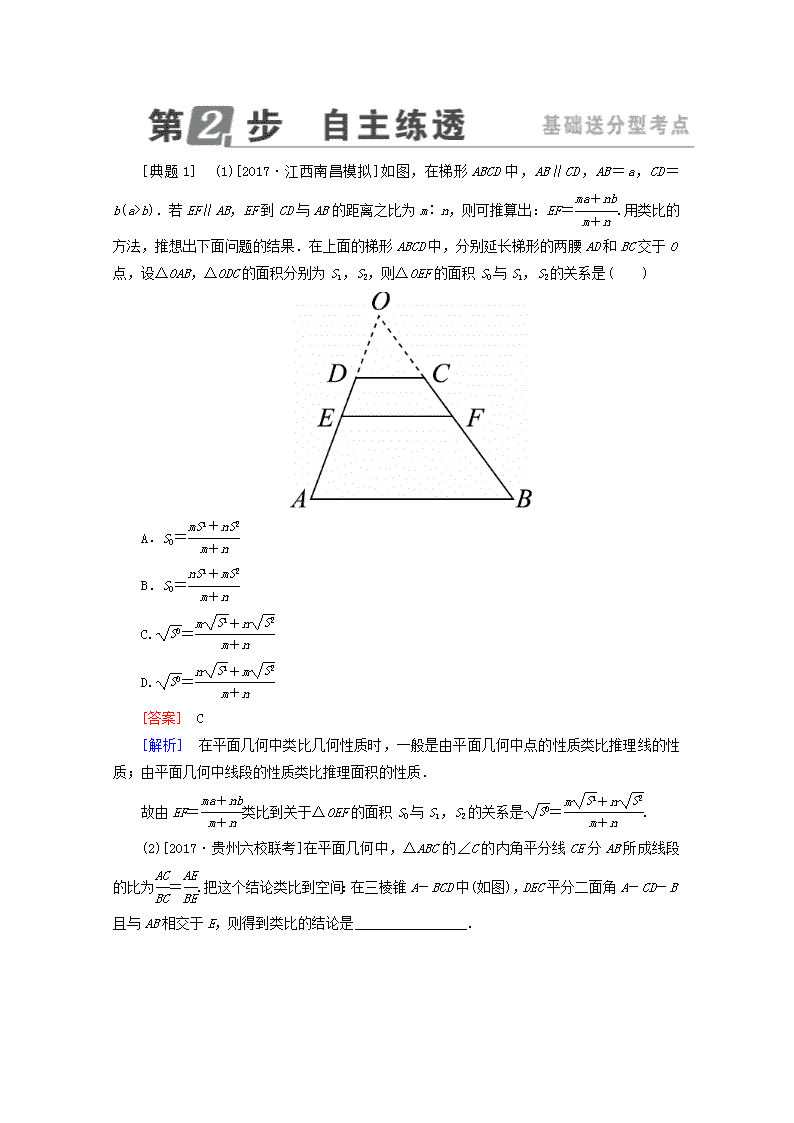
‎§12.1　合情推理与演绎推理 考纲展示►　‎ ‎1.了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发展中的作用．‎ ‎2．了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理．‎ ‎3．了解合情推理和演绎推理之间的联系和差异．‎ 考点1　类比推理 ‎ 　　　　　　 　　　　　 　　　　　‎ 类比推理 ‎(1)①定义：由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有________的推理．‎ ‎(2)特点：是由________到________的推理．‎ 答案：(1)这些特征　(2)特殊　特殊 ‎[教材习题改编]在Rt△ABC中，两直角边分别为a，b，设h为斜边上的高，则＝＋.由此类比：三棱锥S－ABC中的三条侧棱SA，SB，SC两两垂直，且长度分别为a，b，c，设棱锥底面ABC上的高为h，则________．‎ 答案：＝＋＋ 解析：直角三角形的两直角边对应该三棱锥的三条两两垂直的侧棱，直角三角形斜边上的高对应该三棱锥底面上的高，类比得＝＋＋.‎ 事实上，在直角三角形中＝＋是由等面积法得到的，而在三棱锥中可由等体积法求得＝＋＋ ‎[典题1]　(1)[2017·江西南昌模拟]如图，在梯形ABCD中，AB∥CD，AB＝a，CD＝b(a>b)．若EF∥AB，EF到CD与AB的距离之比为m∶n，则可推算出：EF＝.用类比的方法，推想出下面问题的结果．在上面的梯形ABCD中，分别延长梯形的两腰AD和BC交于O点，设△OAB，△ODC的面积分别为S1，S2，则△OEF的面积S0与S1，S2的关系是(　　)‎ A．S0＝ ‎ B．S0＝ C.＝ ‎ D.＝ ‎[答案]　C ‎[解析]　在平面几何中类比几何性质时，一般是由平面几何中点的性质类比推理线的性质；由平面几何中线段的性质类比推理面积的性质．‎ 故由EF＝类比到关于△OEF的面积S0与S1，S2的关系是＝.‎ ‎(2)[2017·贵州六校联考]在平面几何中，△ABC的∠C的内角平分线CE分AB所成线段的比为＝.把这个结论类比到空间：在三棱锥A－BCD中(如图)，DEC平分二面角A－CD－B且与AB相交于E，则得到类比的结论是________________．‎ ‎[答案]　＝ ‎[解析]　由平面中线段的比转化为空间中面积 的比可得，＝.‎ ‎[点石成金]　类比推理的分类及处理方法 类别 解读 适合题型 类比定义 在求解由某种熟悉的定义产生的类比推理型试题时，可以借助原定义来求解 已知熟悉定义类比新定义 类比性质 从一个特殊式子的性质、一个特殊图形的性质入手，提出类比推理型问题，求解时要认真分析两者之间的联系与区别，深入思考两者的转化过程是求解的关键 平面几何与立体几何、等差数列与等比数列 类比方法 有一些处理问题的方法具有类比性，可以把这种方法类比应用到其他问题的求解中，注意知识的迁移 已知熟悉的处理方法类比未知问题的处理方法 考点2　归纳推理 归纳推理 ‎(1)定义：由某类事物的部分对象具有某些特征，推出该类事物的________都具有这些特征的推理，或者由个别事实概括出一般结论的推理．‎ ‎(2)特点：是由________到________、由________到________的推理．‎ 答案：(1)全部对象 ‎(2)部分　整体　个别　一般 ‎(1)[教材习题改编]若数列{an}满足a1＝1，an＋1＝(n∈N*)，则归纳出该数列的通项公式为________．‎ 答案：an＝(n∈N*)‎ 解析：由a1＝1，an＋1＝，得a2＝，a3＝，a4＝，…，‎ 归纳猜想an＝(n∈N*)．‎ ‎(2)[教材习题改编]观察下列不等式：1>，1＋＋>1,1＋＋＋…＋>，1＋＋＋… ＋>2,1＋＋＋… ＋>，…，由此猜测第n个不等式为________________(n∈N*)．‎ 答案：1＋＋＋…＋> 解析：观察得出规律，左边为2n－1个连续自然数的倒数和，右边的数分母为2、分子为n，由此可以猜测第n个不等式为1＋＋＋…＋>.‎ 合情推理的两种常见方法：归纳；类比．‎ ‎(1)数列2,5,11,20，x,47，… 中的x等于________．‎ 答案：32‎ 解析：观察数列前几项，有5－2＝3,11－5＝6,20－11＝9，‎ 由此可归纳得出x－20＝12，即x＝32.‎ ‎(2)若等差数列{an}的首项为a1，公差为d，前n项的和为Sn，则数列 为等差数列，且通项为＝a1＋(n－1)·.类似地，若各项均为正数的等比数列{bn}的首项为b1，公比为q，前n项的积为Tn，则________．‎ 答案：数列 为等比数列，且通项为＝b1()n－1‎ 解析：类比等差数列的结论，得数列 为等比数列，且通项为＝b1()n－1.‎ ‎[考情聚焦]　归纳推理是发现问题、找出规律的具体鲜明的方法，也是创新的一种思维方式，因而成为高考考查的亮点，常以选择题、填空题的形式出现．‎ 主要有以下几个命题角度：‎ 角度一 数的归纳 ‎[典题2]　(1)两旅客坐火车外出旅游，希望座位连在一起，且有一个靠窗，已知火车上的座位如图所示，则下列座位号码符合要求的应当是(　　)‎ A.48,49 B．62,63 ‎ C．75,76 D．84,85‎ ‎[答案]　D ‎[解析]　由已知图形中座位的排序规律可知，被5除余1的数和能被5整除的座位号靠窗，由于两旅客希望座位连在一起，且有一个靠窗，分析答案中的4组座位号知，只有D符合条件．‎ ‎(2)[2017·陕西模拟]观察下列式子：1,1＋2＋1,1＋2＋3＋2＋1,1＋2＋3＋4＋3＋2＋1，…，由以上可推测出一个一般性结论：对于n∈N*,1＋2＋…＋n＋…＋2＋1＝________.‎ ‎[答案]　n2‎ ‎[解析]　∵1＝12,1＋2＋1＝22,1＋2＋3＋2＋1＝32,1＋2＋3＋4＋3＋2＋1＝42，…，‎ ‎∴归纳可得1＋2＋…＋n＋…＋2＋1＝n2.‎ ‎[点石成金]　解决此类问题时，需要细心观察，寻求相邻项及项与序号之间的关系，同时还要联系相关的知识，如等差数列、等比数列等．‎ 角度二 式的归纳 ‎[典题3]　(1)观察下列等式：‎ ‎(1＋1)＝2×1；‎ ‎(2＋1)(2＋2)＝22×1×3；‎ ‎(3＋1)(3＋2)(3＋3)＝23×1×3×5；‎ ‎…‎ 照此规律，第n个等式可为________．‎ ‎[答案]　(n＋1)(n＋2)(n＋3)…(n＋n)＝2n×1×3×5×…×(2n－1)‎ ‎[解析]　观察规律可知，左边为n项的积，最小项和最大项分别为(n＋1)，(n＋n)，右边为连续奇数之积乘以2n，则第n个等式为(n＋1)(n＋2)(n＋3)…(n＋n)＝2n×1×3×5×…×(2n－1)．‎ ‎(2)已知f(x)＝，f1(x)＝f′(x)，f2(x)＝[f1(x)]′，…，fn＋1(x)＝[fn(x)]′，n∈N*，经计算：f1(x)＝，f2(x)＝，f3(x)＝，…，照此规律，则fn(x)＝________.‎ ‎[答案]　 ‎[解析]　因为f1(x)＝，‎ f2(x)＝，f3(x)＝，…，‎ 所以fn(x)＝.‎ ‎(3)[2017·山东日照模拟]设n为正整数，f(n)＝1＋＋＋…＋，计算得f(2)＝，f(4)>2，f(8)>，f(16)>3，观察上述结果，可推测一般的结论为________．‎ ‎[答案]　f(2n)≥(n∈N*)‎ ‎[解析]　∵f(21)＝，f(22)>2＝，f(23)>，f(24)>，‎ ‎∴归纳，得f(2n)≥(n∈N*)．‎ ‎[点石成金]　1.与数字有关的等式的推理，观察数字特点，找出等式左右两侧的规律及符号后可解．‎ ‎2．与不等式有关的推理，观察每个不等式的特点，注意是纵向看，找到规律后可解．‎ 角度三 形的归纳 ‎[典题4]　(1)[2017·重庆模拟]某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为1,1,2,3,5，则预计第10年树的分枝数为(　　)‎ A．21 B．‎34 C．52 D．55‎ ‎[答案]　D ‎[解析]　因为2＝1＋1,3＝2＋1,5＝3＋2，即从第三项起每一项都等于前两项的和，‎ 所以第10年树的分枝数为21＋34＝55.‎ ‎(2)下面图形由小正方形组成，请观察图①至图④的规律，并依此规律，写出第n个图形中小正方形的个数是________．‎ ‎[答案]　 ‎[解析]　由题图知，第n个图形的小正方形个数为1＋2＋3＋…＋n，∴总个数为.‎ ‎[点石成金]　与图形变化有关的推理的解题策略 合理利用特殊图形归纳推理得出结论，并用赋值检验法验证其真伪性．‎ 考点3　演绎推理 ‎ 　　　　　　 　　　　　 　　　　　‎ ‎1.演绎推理 从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．简言之，演绎推理是由________到________的推理．‎ 答案：一般　特殊 ‎2．“三段论”是演绎推理的一般模式 ‎(1)大前提——已知的________．‎ ‎(2)小前提——所研究的________．‎ ‎(3)结论——根据一般原理，对________做出的判断．‎ 答案：(1)一般原理　(2)特殊情况　(3)特殊情况 演绎推理的两个易错点：推理形式错误；大(小)前提错误．‎ ‎(1)命题“有些有理数是无限循环小数，整数是有理数，所以整数是无限循环小数”是假命题，推理错误的原因是________．‎ ‎(2)“所有是3的倍数的数都是9的倍数，m是3的倍数，则m一定是9的倍数”，这是三段论推理，但其结论是错误的，错误的原因是________．‎ 答案：(1)推理形式错误　(2)大前提错误 解析：(1)大前提与小前提之间没有包含关系，虽然使用了“三段论”，但推理形式错误．‎ ‎(2)因为大前提错误，所以尽管推理的形式正确，结论仍然是错的.‎ ‎[典题5]　已知函数f(x)＝－(a>0，且a≠1)．‎ ‎(1)证明：函数y＝f(x)的图象关于点，－对称；‎ ‎(2)求f(－2)＋f(－1)＋f(0)＋f(1)＋f(2)＋f(3)的值．‎ ‎(1)[证明]　函数f(x)的定义域为全体实数，让取一点(x，y)，它关于点对称的点的坐标为(1－x，－1－y)．‎ 由已知y＝－，‎ 则－1－y＝－1＋＝－，‎ f(1－x)＝－＝－ ‎＝－＝－，‎ ‎∴－1－y＝f(1－x)，即函数y＝f(x)的图象关于点对称．‎ ‎(2)[解]　由(1)知，－1－f(x)＝f(1－x)，‎ 即f(x)＋f(1－x)＝－1.‎ ‎∴f(－2)＋f(3)＝－1，f(－1)＋f(2)＝－1，f(0)＋f(1)＝－1.‎ 故f(－2)＋f(－1)＋f(0)＋f(1)＋f(2)＋f(3)＝－3.‎ ‎[点石成金]　演绎推理是由一般到特殊的推理，常用的一般模式为三段论，演绎推理的前提和结论之间有着某种蕴含关系，解题时要找准正确的大前提．一般地，若大前提不明确时，可找一个使结论成立的充分条件作为大前提．‎ ‎[方法技巧]　1.合情推理的过程 →→→ ‎2．演绎推理是从一般的原理出发，推出某个特殊情况的结论的推理方法，是由一般到特殊的推理，常用的一般模式是三段论．数学问题的证明主要通过演绎推理来进行．‎ ‎[易错防范]　1.在进行类比推理时要尽量从本质上去类比，不要被表面现象迷惑，如果只抓住一点表面现象的相似甚至假象就去类比，那么就会犯机械类比的错误．‎ ‎2．合情推理是从已知的结论推测未知的结论，发现与猜想的结论都要经过进一步严格证明．‎ ‎3．演绎推理是由一般到特殊的推理，它常用来证明和推理数学问题，解题时应注意推理过程的严密性，书写格式的规范性．‎ ‎ 真题演练集训 ‎ ‎1．[2016·北京卷]袋中装有偶数个球，其中红球、黑球各占一半．甲、乙、丙是三个空盒，每次从袋中任意取出两个球，将其中一个球放入甲盒，如果这个球是红球，就将另一个球放入乙盒，否则就放入丙盒．重复上述过程，直到袋中所有球都被放入盒中，则(　　)‎ A．乙盒中黑球不多于丙盒中黑球 B．乙盒中红球与丙盒中黑球一样多 C．乙盒中红球不多于丙盒中红球 D．乙盒中黑球与丙盒中红球一样多 答案：B 解析：‎ 解法一：假设袋中只有一红一黑两个球，第一次取出后，若将红球放入了甲盒，则乙盒中有一个黑球，丙盒中无球，A错误；若将黑球放入了甲盒，则乙盒中无球，丙盒中有一个红球，D错误；同样，假设袋中有两个红球和两个黑球，第一次取出两个红球，则乙盒中有一个红球，第二次必然拿出两个黑球，则丙盒中有一个黑球，此时乙盒中红球多于丙盒中的红球，C错误．故选B.‎ 解法二：设袋中共有2n个球，最终放入甲盒中k个红球，放入乙盒中s个红球．依题意知，甲盒中有(n－k)个黑球，乙盒中共有k个球，其中红球有s个，黑球有(k－s)个，丙盒中共有(n－k)个球，其中红球有(n－k－s)个，黑球有(n－k)－(n－k－s)＝s(个)．所以乙盒中红球与丙盒中黑球一样多．故选B.‎ ‎2．[2014·北京卷]学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，那么这组学生最多有(　　)‎ A．2人 B．3人 C．4人 D．5人 答案：B 解析：设学生人数为n，因为成绩评定只有“优秀”“合格”“不合格”三种情况，所以当n≥4时，语文成绩至少有两人相同，若此两人数学成绩也相同，与“任意两人成绩不全相同”矛盾；若此两人数学成绩不同，则此两人有一人比另一人成绩好，也不满足条件，因此：n＜4，即n≤3.当n＝3时，评定结果分别为“优秀，不合格”“合格，合格”“不合格，优秀”，符合题意，故n＝3，故选B.‎ ‎3．[2015·山东卷]观察下列各式：‎ C＝40；‎ C＋C＝41；‎ C＋C＋C＝42；‎ C＋C＋C＋C＝43；‎ ‎……‎ 照此规律，当n∈N*时，‎ C＋C＋C＋…＋C＝________.‎ 答案：4n－1‎ 解析：由题知，‎ C＋C＋C＋…＋C＝4n－1.‎ ‎4．[2015·福建卷]一个二元码是由0和1组成的数字串x1x2…xn(n∈N*)，其中xk(k＝1,2，…，n)称为第k位码元．二元码是通信中常用的码，但在通信过程中有时会发生码元错误(即码元由0变为1，或者由1变为0)．‎ 已知某种二元码x1x2…x7的码元满足如下校验方程组：‎ 其中运算⊕定义为：0⊕0＝0,0⊕1＝1,1⊕0＝1,1⊕1＝0.‎ 现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101，那么利用上述校验方程组可判定k等于________．‎ 答案：5‎ 解析：设a，b，c，d∈{0,1}，在规定运算法则下满足：a⊕b⊕c⊕d＝0，可分为下列三类情况：①4个1：1⊕1⊕1⊕1⊕＝0，②2个1：1⊕1⊕0⊕0＝0，③0个1：0⊕0⊕0⊕0＝0，因此，错码1101101通过校验方程组可得：‎ 由x4⊕x5⊕x6⊕x7＝0，∴1⊕1⊕0⊕1≠0；‎ 由x2⊕x3⊕x6⊕x7＝0，∴1⊕0⊕0⊕1＝0；‎ 由x1⊕x3⊕x5⊕x7＝0，∴1⊕0⊕1⊕1≠0.‎ ‎∴错码可能出现在x5上或x1与x4都错．‎ 由已知只有第k位发生码元错误，故错误为x5，‎ 若x5＝0，则检验方程组都成立，故k＝5.‎ ‎5．[2014·新课标全国卷Ⅰ]甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，‎ 甲说：我去过的城市比乙多，但没去过B城市；‎ 乙说：我没去过C城市；‎ 丙说：我们三人去过同一城市．‎ 由此可判断乙去过的城市为________．‎ 答案：A 解析：由于甲、乙、丙三人去过同一城市，而甲没有去过B城市，乙没有去过C城市，因此三人去过的同一城市应为A，而甲去过的城市比乙多，但没去过B城市，所以甲去过的城市数应为2，乙去过的城市应为A.‎ ‎ 课外拓展阅读 ‎ 归纳不准确致误分析 ‎[典例]　如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项，如表所示．‎ a1‎ a2‎ a3‎ a4‎ a5‎ a6‎ a7‎ a8‎ a9‎ a10‎ a11‎ a12‎ x1‎ y1‎ x2‎ y2‎ x3‎ y3‎ x4‎ y4‎ x5‎ y5‎ x6‎ y6‎ 按如此规律下去，则a2 013＋a2 014＋a2 015等于(　　)‎ A．1 004 B．1 ‎007 C．1 011 D．2 014‎ ‎[易错分析]　本题中的“按如此规律下去”就是要求由题目给出的6个点的坐标和数列的对应关系，归纳出该数列的一般关系．可能出现的错误有两种：一是归纳时找不准“前几项”的规律，胡乱猜测；二是弄错奇、偶项的关系．本题中各个点的纵坐标对应数列的偶数项，并且逐一递增，即a2n＝n(n∈N*)，各个点的横坐标对应数列的奇数项，正负交替后逐一递增，并且满足a4n－3＋a4n－1＝0(n∈N*)，如果弄错这些关系就会得到错误的结果，如认为当n为偶数时an＝n，就会得到a2 013＋a2 014＋a2 015＝2 014的错误结论，而选D.‎ ‎[解析]　a1＝1，a2＝1，a3＝－1，a4＝2，a5＝2，a6＝3，a7＝－2，a8＝4，…，这个数列的规律是奇数项为1，－1,2，－2,3，…，偶数项为1,2,3，…，故a2 013＋a2 015＝0，a2 014＝1 007，故a2 013＋a2 014＋a2 015＝1 007.‎ ‎[答案]　B 归纳总结 由归纳推理得到的结论具有猜测的性质，结论是否真实，还需经过逻辑证明和实践检验．因此，它不能作为数学证明的工具．‎