数学（理）卷·2018届宁夏银川一中高三下学期第一次模拟考试（2018

数学（理）卷·2018届宁夏银川一中高三下学期第一次模拟考试（2018

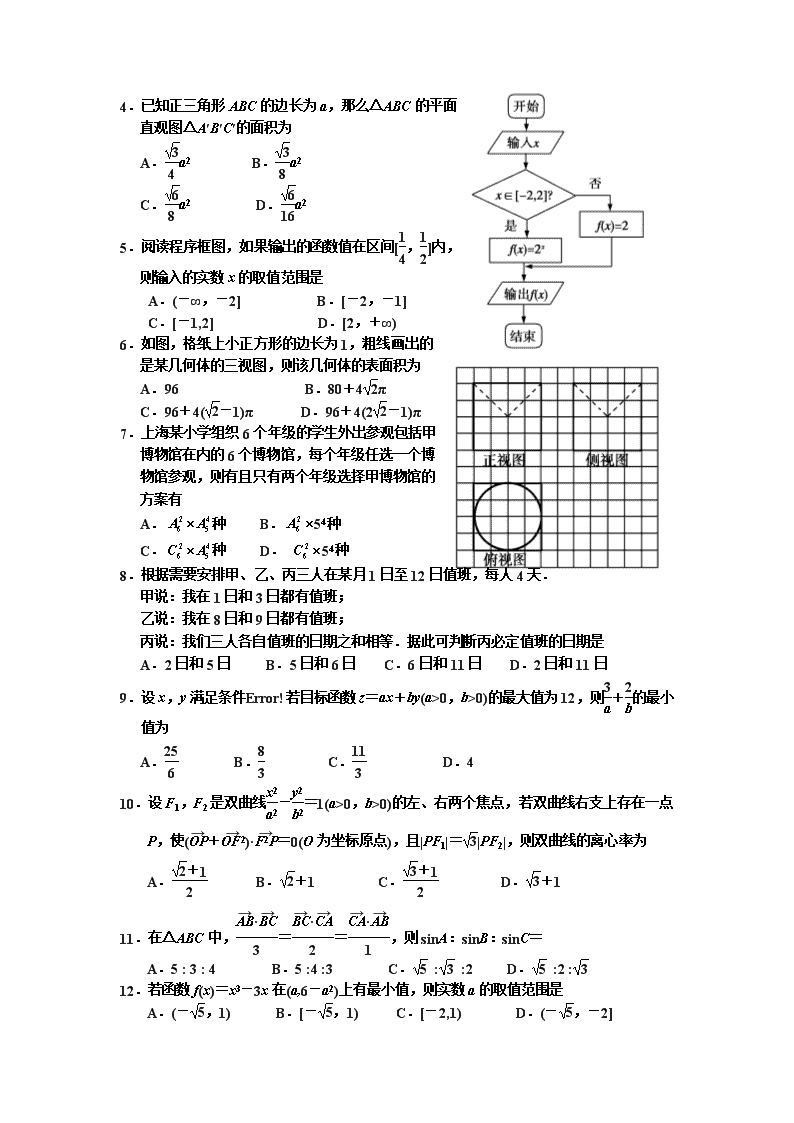
绝密★启用前 ‎2018年普通高等学校招生全国统一考试 理 科 数 学 ‎(银川一中第一次模拟考试)‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～23题为选考题，其它题为必考题。考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试结束后，将本试卷和答题卡一并交回。‎ 注意事项：‎ ‎1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。‎ ‎2．选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案的标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎3．考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。‎ ‎4．保持卡面清洁，不折叠，不破损。‎ ‎5．做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑。‎ 第I卷 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的． ‎ ‎1．已知复数z＝ －2i (其中i为虚数单位)，则|z|＝‎ A．3 B．‎3 ‎ C．2 D．2 ‎2．设集合A＝{(x，y)|x2＋y2＝1}，B＝{(x，y)|y＝3x}，则A∩B的子集的个数是 A．4 B．‎3 ‎C．2 D．1‎ ‎3．古代数学著作《九章算术》有如下问题：“今有女子善织，日自倍，五日织五尺，问日织几何？”意思是：“一女子善于织布，每天织的布都是前一天的2倍，已知她5天共织布5尺，问这女子每天分别织布多少？”根据上题的已知条件，可求得该女子第3天所织布的尺数为 A． B． C． D． ‎4．已知正三角形ABC的边长为a，那么△ABC的平面 直观图△A′B′C′的面积为 A．a2 B．a2 ‎ C．a2 D．a2‎ ‎5．阅读程序框图，如果输出的函数值在区间[，]内，‎ 则输入的实数x的取值范围是 A．(－∞，－2] B．[－2，－1] ‎ C．[－1,2] D．[2，＋∞)‎ ‎6．如图，格纸上小正方形的边长为1，粗线画出的 是某几何体的三视图，则该几何体的表面积为 A．96 B．80＋4π ‎ C．96＋4(－1)π D．96＋4(2－1)π ‎7．上海某小学组织6个年级的学生外出参观包括甲 博物馆在内的6个博物馆，每个年级任选一个博 物馆参观，则有且只有两个年级选择甲博物馆的 方案有 A．种 B．54种 ‎ C．种 D． 54种 ‎8．根据需要安排甲、乙、丙三人在某月1日至12日值班，每人4天．‎ 甲说：我在1日和3日都有值班；‎ 乙说：我在8日和9日都有值班；‎ 丙说：我们三人各自值班的日期之和相等．据此可判断丙必定值班的日期是 A．2日和5日 B．5日和6日 C．6日和11日 D．2日和11日 ‎9．设x，y满足条件若目标函数z＝ax＋by(a>0，b>0)的最大值为12，则＋的最小值为 A． B． C． D．4‎ ‎10．设F1，F2是双曲线－＝1(a>0，b>0)的左、右两个焦点，若双曲线右支上存在一点P，使(＋)·＝0(O为坐标原点)，且|PF1|＝|PF2|，则双曲线的离心率为 A． B．＋‎1 C． D．＋1‎ ‎11．在△ABC中，＝＝，则sinA：sinB：sinC＝‎ A．5 : 3 : 4 B．5 :4 :‎3 C． : :2 D． :2 : ‎12．若函数f(x)＝x3－3x在(a,6－a2)上有最小值，则实数a的取值范围是 A．(－，1) B．[－，1) C．[－2,1) D．(－，－2]‎ 第Ⅱ卷 本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第23题为选考题，考生根据要求做答．‎ 二、填空题：本大题共4小题，每小题5分.‎ ‎13．若a＝log43，则‎2a＋2－a ＝ .‎ ‎14．函数f(x)＝2sin2(＋x)－cos2x （≤x≤）的值域为 .‎ ‎15．已知圆x2＋y2＝4, B(1,1)为圆内一点，P,Q为圆上动点，若PBQ=900，则线段PQ中点的轨迹方程为 .‎ ‎16．设O为坐标原点，P是以F为焦点的抛物线y2＝2px(p>0)上任意一点，M是线段PF上的点，且|PM|＝2|MF|，则直线OM的斜率的最大值为 .‎ 三．解答 ‎17．(本小题满分12分)‎ 设Sn为数列{an}的前n项和，已知an＞0，a＋2an＝4Sn＋3.‎ ‎(1)求{an}的通项公式：‎ ‎(2)设bn＝，求数列{bn}的前n项和．‎ ‎18．(本小题满分12分)‎ 人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间[0,10]内的一个数来表示，该数越接近10表示满意度越高．为了解某地区居民的幸福感情况，随机对该地区的男、女居民各500人进行了调查，调查数据如表所示：‎ 幸福感指数 ‎[0,2)‎ ‎[2,4)‎ ‎[4,6)‎ ‎[6,8)‎ ‎[8,10]‎ 男居民人数 ‎10‎ ‎20‎ ‎220‎ ‎125‎ ‎125‎ 女居民人数 ‎10‎ ‎10‎ ‎180‎ ‎175‎ ‎125‎ ‎(1)在图中绘出频率分布直方图 ‎（说明：将各个小矩形纵坐标标注 在相应小矩形边的最上面），并估算 该地区居民幸福感指数的平均值；‎ ‎(2)若居民幸福感指数不小于6，‎ 则认为其幸福．为了进一步了解居 民的幸福满意度，调查组又在该地 区随机抽取4对夫妻进行调查，用 X表示他们之中幸福夫妻(夫妻二人 都感到幸福)的对数，求X的分布列及期望(以样本的频率作为总体的概率)．‎ ‎19.(本小题满分12分)‎ 如图，在四棱锥P－ABCD中，PA⊥面ABCD，AD∥BC，‎ ‎∠BAD＝90°，AC⊥BD，BC＝1，AD＝PA＝2，E，F分别为PB，‎ AD的中点.‎ ‎(1)证明：AC⊥EF；‎ ‎(2)求直线EF与平面PCD所成角的正弦值．‎ ‎20．(本小题满分12分)‎ 已知椭圆的离心率，连接椭圆的四个顶点得到的菱形的面积为4.‎ ‎(1)求椭圆的方程.‎ ‎(2)设直线与椭圆相交于不同的两点，已知点的坐标为（），点在线段的垂直平分线上，且，求的值.‎ ‎21.(本小题满分12分)‎ 已知函数f(x)＝lnx－ax2＋(a－2)x.‎ ‎(1)若f(x)在x＝1处取得极值，求a的值；‎ ‎(2)求函数y＝f(x)在[a2，a]上的最大值．‎ 请考生在第22-23题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．(本小题满分10分) 选修4-4：坐标系与参数方程 在直角坐标系xOy中，曲线C1的参数方程为(α为参数)，曲线C2的参数方程为(β为参数)，以O为极点，x轴的正半轴为极轴建立极坐标系.‎ ‎(1)求曲线C1和曲线C2的极坐标方程；‎ ‎(2)已知射线l1：θ＝α(0<α<)，将射线l1顺时针旋转得到射线l2：θ＝α－，且射线l1与曲线C1交于O，P两点，射线l2与曲线C2交于O，Q两点，求|OP|·|OQ|的最大值．‎ ‎23．（本小题满分10分）选修4—5；不等式选讲．‎ ‎ 设不等式的解集为M，且 ‎（1）证明：；‎ ‎（2）比较与的大小，并说明理由.‎ 宁夏银川一中2018届高三第一次模拟数学(理科)参考答案及评分标准 一．选择 ‎1．B 解：z＝－2i＝－2i＝3－i－2i＝3－3i，则|z|＝3，故选B．‎ ‎2．A 解：∵集合A＝{(x，y)|x2＋y2＝1}，B＝{(x，y)|y＝3x}∴x2＋y2＝1圆和指数函数y＝3x图象，如图，可知其有两个不同交点，记为A1、A2则A∩B的子集应为∅，{A1}，{A2}，{A1，A2}共四种，故选A.‎ ‎3．A 解：设这女子每天分别织布an尺，则数列{an}是等比数列，公比q＝2．则＝5，解得a1＝．∴a3＝×22＝.故选A．‎ ‎4．D [解析]　如图①、②所示的平面图形和直观图．‎ 由②可知，A′B′＝AB＝a，O′C′＝OC＝a，在图②中作 C′D′⊥A′B′于D′，则C′D′＝O′C′＝a.∴S△A′B′C′＝A′B′·C′D′＝×a×a＝a2.‎ ‎5. B[解析]　该程序的作用是计算分段函数f(x)＝的函数值．又∵输出的函数值在区间[，]内，∴x∈[－2，－1]，故选B．‎ ‎6. C 解：由三视图可知几何体为边长为4的正方体挖去一个圆锥得到的，圆锥的底面半径为2，高为2，∴圆锥的母线长为2.∴几何体的平面部分面积为6×42﹣π×22＝96﹣4π.圆锥的侧面积为π×2×2＝4π.∴几何体的表面积为96﹣4π＋4π.故选C．‎ ‎7．D [解析] 因为有且只有两个年级选择甲博物馆，所以参观甲博物馆的年级有C种情况，其余年级均有5种选择，所以共有54种情况，根据乘法原理可得C×54种情况，故选D．‎ ‎8．C　[解析]　1～12日期之和为78，三人各自值班的日期之和相等，故每人值班四天的日期之和是26，甲在1日和3日都有值班，故甲余下的两天只能是10号和12号；而乙在8日和9日都有值班，8＋9＝17，所以11号只能是丙去值班了．余下还有2号、4号、5号、6号、7号五天，显然，6号只可能是丙去值班了．‎ ‎9. D [解析]　不等式组表示的平面区域为如图所示的阴影部分．‎ 当直线ax＋by＝z(a>0，b>0)过直线x－y＋2＝0与直线3x－y－6＝0‎ 的交点(4,6)时，目标函数z＝ax＋by(a>0，b>0)取得最大值12，‎ ‎∴‎4a＋6b＝12，即‎2a＋3b＝6．‎ ‎∴＋＝(＋)·＝(12＋＋)≥4，当且仅当＝，‎ 即a＝，b＝1时，等号成立．∴＋的最小值为4，故选D．‎ ‎10. D　[解析]　∵(＋)·＝0，∴(＋)·(－)＝0，∴2－2＝0，OP＝OF2＝c＝OF1，∴PF1⊥PF2，Rt△PF‎1F2中，∵|PF1|＝|PF2|，∴∠PF‎1F2＝30°.由双曲线的定义得PF1－PF2＝‎2a，∴PF2＝，sin30°＝＝＝＝，∴‎2a＝c(－1)，∴＝＋1，故选D．‎ ‎11. C [解析]　由条件利用两个向量的数量积的定义可得‎2a2＋‎2c2－2b2＝‎3a2＋3b2－‎3c2＝6b2＋‎6c2－‎6a2＝k，由此求得a、b、c的值，利用正弦定理可得sinA：sinB：sinC的值．解：△ABC中，∵＝＝，∴＝＝即＝＝，即·＝·＝bc，即 ‎2a2＋‎2c2－2b2＝‎3a2＋3b2－‎3c2＝6b2＋‎6c2－‎6a2，设‎2a2＋‎2c2－2b2＝‎3a2＋3b2－‎3c2＝6b2＋‎6c2－‎6a2＝k，求得 a2＝5k，b2＝3k，c2＝4k，∴a＝k，b＝k，c＝＝2，∴由正弦定理可得a：b：c＝sinA：sinB：sinC＝::2，故选C．‎ ‎12．C　[解析]　f′(x)＝3x2－3＝0，解得x＝±1，且x＝1为函数的极小值点，x＝－1为函数的极大值点．因为函数f(x)在区间(a,6－a2)上有最小值，所以函数f(x)的极小值点必在区间(a,6－a2)内，即实数a满足a<1<6－a2，且f(a)＝a3－‎3a≥f(1)＝－2.由a<1<6－a2，解得－0，‎ 此时x＝1是函数f(x)的极小值点，所以a＝－1.‎ ‎(2)因为a20，所以f(x)在(0，)上单调递增，在(，＋∞)上单调递减．‎ ‎①当0

查看更多