海南省海南枫叶国际学校2019-2020学年高二上学期期末考试数学试题

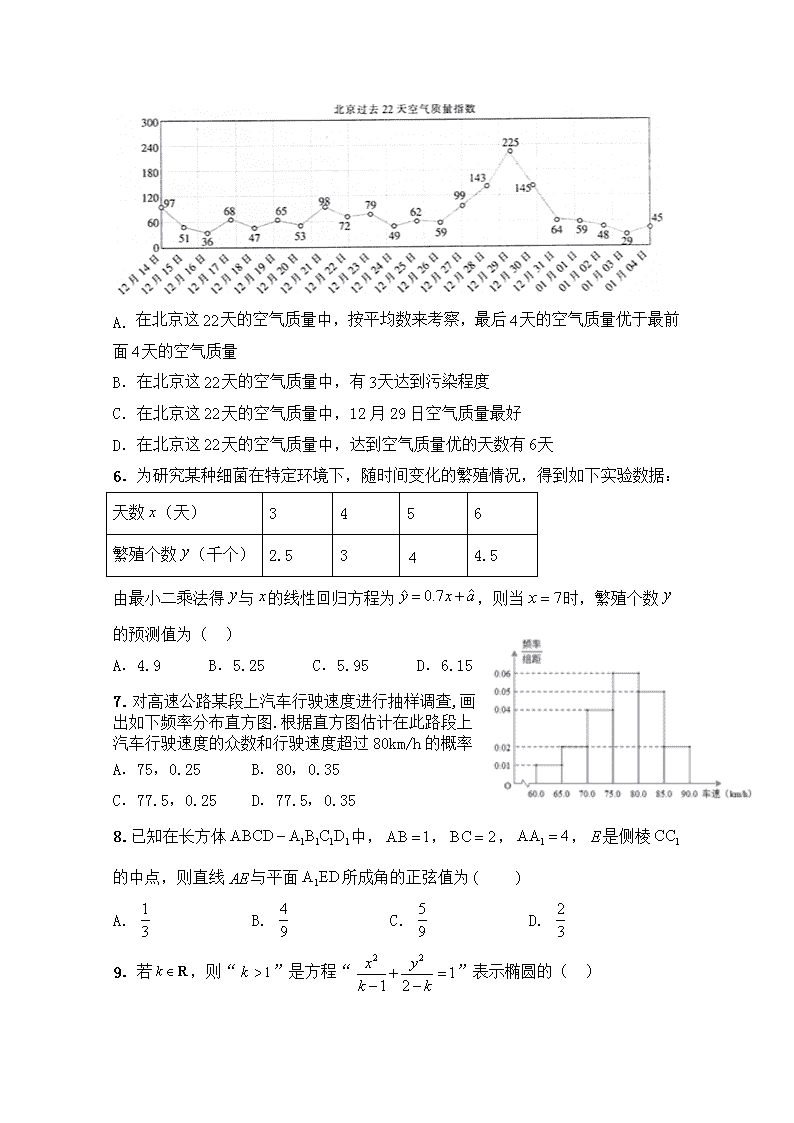
海南省海南枫叶国际学校2019-2020学年高二上学期期末考试数学试题

海南枫叶国际学校2019-2020学年度第一学期高二年级 数学学科期末考试试卷 命题者： ‎ 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡 第I卷（选择题)‎ 一、单选题（每小题5分，共60分）‎ ‎1．某中学初一、初二、初三的学生人数分别为500,600,700,现用分层抽样的方法从这三个年级中选取18人参加学校的演讲比赛,则应选取的初二年级学生人数为( )‎ A．5 B．‎6 ‎C．7 D．8‎ ‎2．若对于变量的取值为3，4，5，6，7时，变量对应的值依次分别为4.0，2.5，-0.5，-1，-2；若对于变量的取值为1，2，3，4时，变量对应的值依次分别为2，3，4，6，则变量和，变量和的相关关系是（ ）‎ A．变量和是正相关，变量和是正相关 ‎ B．变量和是正相关，变量和是负相关 C．变量和是负相关，变量和是负相关 ‎ D．变量和是负相关，变量和是正相关 ‎3．我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为（ ）‎ A．134石 B．169石 C．338石 D．1365石 ‎4．已知随机事件和互斥，且，，则（ ）‎ A．0.5 B．‎0.1 ‎C．0.7 D．0.8‎ ‎5．空气质量指数（简称：）是定量描述空气质量状况的无量纲指数，空气质量按照大小分为六级：为优，为良，为轻度污染，为中度污染，为重度污染，为严重污染.下面记录了北京市天的空气质量指数，根据图表，下列结论错误的是（ ）‎ A． 在北京这天的空气质量中，按平均数来考察，最后天的空气质量优于最前面天的空气质量 B．在北京这天的空气质量中，有天达到污染程度 C．在北京这天的空气质量中，‎12月29日空气质量最好 ‎ D．在北京这天的空气质量中，达到空气质量优的天数有天 ‎6．为研究某种细菌在特定环境下，随时间变化的繁殖情况，得到如下实验数据：‎ 天数（天）‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 繁殖个数（千个）‎ ‎2.5‎ ‎3‎ ‎4.5‎ 由最小二乘法得与的线性回归方程为，则当时，繁殖个数的预测值为（ ）‎ A．4.9 B．‎5.25 C．5.95 D．6.15‎ ‎7．对高速公路某段上汽车行驶速度进行抽样调查,画出如下频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过‎80km/h的概率 A．75，0.25 B．80，0.35 ‎ C．77.5，0.25 D．77.5，0.35‎ ‎8．已知在长方体中，，，，是侧棱的中点，则直线与平面所成角的正弦值为　　‎ A． B． C． D．‎ ‎9．若，则“”是方程“”表示椭圆的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎10．已知F是抛物线y2＝x的焦点，A，B是该抛物线上的两点，|AF|＋|BF|＝3，则线段AB的中点D到y轴的距离为(　　)‎ A． B．‎1 C． D． ‎11．如图，已知椭圆C的中心为原点O，F(－2，0)为C的左焦点，P为C上一点，满足|OP|＝|OF|，且|PF|＝4，则椭圆C的方程为(　　)‎ A．＋＝1　　　B．＋＝‎1 C．＋＝1 D．＋＝1‎ ‎12．已知是双曲线的左右焦点，过作双曲线一条渐近线的垂线，垂足为点,交另一条渐近线于点，且,则该双曲线的离心率为 A． B． C． D．‎ 第II卷（非选择题)‎ 二、填空题（每小题5分，共20分）‎ ‎13．命题“”的否定是________.‎ ‎14．总体由编号为的个个体组成，利用随机数表（以下选取了随机数表中的第行和第行）选取个个体，选取方法是从随机数表第行的第列开始由左向右读取，则选出来的第个个体的编号为______________；‎ ‎15．已知双曲线与椭圆有相同的焦点，且双曲线的渐进线方程为，则此双曲线方程为_________‎ ‎16．如图所示，在四边形中，,将四边形沿对角线折成四面体，使平面平面 ‎，则下列结论正确的是 ．‎ ‎（1）； （2）；‎ ‎（3）与平面所成的角为；‎ ‎（4）四面体的体积为．‎ 三、解答题（17题10分，其余每小题12分，共60分）‎ ‎17．如图，ABCD是正方形，O是正方形的中心，‎ 面ABCD，E是PC的中点．‎ 求证:（1）平面BDE；‎ ‎（2）平面平面BDE．‎ ‎18．年月日是第二十七届“世界水日”，月日是第三十二届“中国水周”．我国纪念年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先，强化水资源管理”．某中学课题小组抽取、两个小区各户家庭，记录他们月份的用水量（单位：）如下表：‎ 小区家庭月用水量 小区家庭月用水量 ‎（1）根据两组数据完成下面的茎叶图，从茎叶图看，哪个小区居民节水意识更好？‎ ‎（2）从用水量不少于的家庭中，、两个小区各随机抽取一户，求小区家庭的用水量低于小区的概率．‎ ‎19．某校学生社团组织活动丰富，学生会为了解同学对社团活动的满意程度，随机选取了100位同学进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照[40，50），[50，60），[60，70），…，[90，100]分成6组，制成如图所示频率分布直方图．‎ ‎（1）求图中x的值；‎ ‎（2）求这组数据的中位数；‎ ‎（3）现从被调查的问卷满意度评分值在[60，80）的学生中按分层抽样的方法抽取5人进行座谈了解，再从这5人中随机抽取2人作主题发言，求抽取的2人恰在同一组的概率．‎ ‎20．在直三棱柱中，底面是直角三角形，，为侧棱的中点.‎ ‎（1）求异面直线、所成角的余弦值；‎ ‎（2）求二面角的平面角的余弦值.‎ ‎21．已知点，直线，动点到点的距离等于它到直线的距离．‎ ‎(Ⅰ)试判断点的轨迹的形状，并写出其方程；‎ ‎(Ⅱ)若曲线与直线相交于两点，求的面积.‎ ‎22．焦点在x轴上的椭圆C：经过点，椭圆C的离心率为．，是椭圆的左、右焦点，P为椭圆上任意点．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若点M为的中点（O为坐标原点），过M且平行于OP的直线l交椭圆C于A，B两点，是否存在实数，使得；若存在，请求出的值，若不存在，请说明理由．‎ 海南枫叶国际学校2019-2020学年度第一学期 高二年级数学学科期末考试答案 一、单选题 BDBA CBDB BCDA 第II卷（非选择题)‎ 二、填空题（每小题5分，共20分）‎ ‎13．‎ ‎14．‎ ‎15．‎ ‎16．（2）（4）‎ 三、解答题 ‎17．如图，ABCD是正方形，O是正方形的中心，面ABCD，E是PC的中点．‎ 求证:（1）平面BDE；‎ ‎（2）平面平面BDE．‎ ‎【解析】‎ ‎（1）连接 是正方形的中心 为中点，又为中点 ‎ 平面，平面 平面 ‎（2）是正方形的中心 ‎ 平面，平面 ‎ 平面， 平面 平面 平面平面 ‎18．年月日是第二十七届“世界水日”，月日是第三十二届“中国水周”．我国纪念年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先，强化水资源管理”．某中学课题小组抽取、两个小区各户家庭，记录他们月份的用水量（单位：）如下表：‎ 小区家庭月用水量 小区家庭月用水量 ‎（1）根据两组数据完成下面的茎叶图，从茎叶图看，哪个小区居民节水意识更好？‎ ‎（2）从用水量不少于的家庭中，、两个小区各随机抽取一户，求小区家庭的用水量低于小区的概率．‎ ‎【解析】‎ ‎（1）绘制如下茎叶图：‎ 由以上茎叶图可以看出，小区月用水量有的叶集中在茎、上，而小区月用水量有的叶集中在茎、上，由此可看出小区居民节水意识更好；‎ ‎（2）从用水量不少于的家庭中，、两个小区各随机抽取一户的结果：‎ ‎、、、、、、、，共个基本事件，‎ 小区家庭的用水量低于小区的的结果：、、，共个基本事件．‎ 所以，小区家庭的用水量低于小区的概率是．‎ ‎19．某校学生社团组织活动丰富，学生会为了解同学对社团活动的满意程度，随机选取了100位同学进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照[40，50），[50，60），[60，70），…，[90，100]分成6组，制成如图所示频率分布直方图．‎ ‎（1）求图中x的值；‎ ‎（2）求这组数据的中位数；‎ ‎（3）现从被调查的问卷满意度评分值在[60，80）的学生中按分层抽样的方法抽取5人进行座谈了解，再从这5人中随机抽取2人作主题发言，求抽取的2人恰在同一组的概率．‎ ‎【解析】‎ 解：（1）由（0.005+0.010+0.030+0.025+0.010+x）×10=1，解得x=0. 02．‎ ‎（2）中位数设为m，则0.05+0.1+0.2+（m-70）×0.03=0.5，解得m=75．‎ ‎（3）可得满意度评分值在[60，70）内有20人，抽得样本为2人，记为a1，a2 ‎ 满意度评分值在[70，80）内有30人，抽得样本为3人，记为b1，b2，b3，‎ 记“5人中随机抽取2人作主题发言，抽出的2人恰在同一组”为事件A，‎ 基本事件有（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a2，b1），（a2，b2），‎ ‎（a2，b3），（b1，b2），（b1，b3），（b2，b3）共10个，A包含的基本事件个数为4个，‎ 利用古典概型概率公式可知P（A）=0.4．‎ ‎20．在直三棱柱中，底面是直角三角形，，为侧棱的中点.‎ ‎（1）求异面直线、所成角的余弦值；‎ ‎（2）求二面角的平面角的余弦值.‎ ‎【解析】‎ ‎（1）如图所示，以C为原点，CA、CB、CC1为坐标轴，建立空间直角坐标系C-xyz 则C(0，0，0)，A(2，0，0)，B(0，2，0)，C1(0，0，2)，B1(0，2，2)，D(2，0，1).‎ 所以，，‎ 所以.即异面直线DC1与B‎1C所成角的余弦值为.‎ ‎（2）因为，，，所以，，所以为平面ACC‎1A1的一个法向量。‎ 因为，，设平面B1DC1的一个法向量为，(x,y,z).‎ 由得令x＝1，则y＝2，z＝－2，＝(1,2,－2).‎ 所以所以二面角B1―DC―C1的余弦值为 ‎21．已知点，直线，动点到点的距离等于它到直线的距离．‎ ‎(Ⅰ)试判断点的轨迹的形状，并写出其方程；‎ ‎(Ⅱ)若曲线与直线相交于两点，求的面积.‎ ‎【解析】‎ ‎（Ⅰ）因点到点的距离等于它到直线的距离，所以点的轨迹是以为焦点、直线为准线的抛物线，其方程为；‎ ‎（Ⅱ）设, 联立，得 , , ‎ 直线经过抛物线的焦点, ‎ 点到直线的距离，‎ ‎22．焦点在x轴上的椭圆C：经过点，椭圆C的离心率为．，是椭圆的左、右焦点，P为椭圆上任意点．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若点M为的中点（O为坐标原点），过M且平行于OP的直线l交椭圆C于A，B两点，是否存在实数，使得；若存在，请求出的值，若不存在，请说明理由．‎ ‎【解析】‎ 解：（1）由已知可得，解得，，‎ 所以椭圆的标准方程为．‎ ‎（2）若直线的斜率不存在时，，，‎ 所以；‎ 当斜率存在时，设直线的方程为，，．‎ 联立直线与椭圆方程，消去y，得，‎ 所以．‎ 因为，设直线的方程为，‎ 联立直线与椭圆方程，消去，得，解得．‎ ‎，‎ ‎，‎ 同理，，‎ 因为，‎ ‎，故，存在满足条件，‎ 综上可得，存在满足条件．‎