2020届二轮复习第8讲　空间中的平行与垂直课件（22张）（江苏专用）

2020届二轮复习第8讲　空间中的平行与垂直课件（22张）（江苏专用）

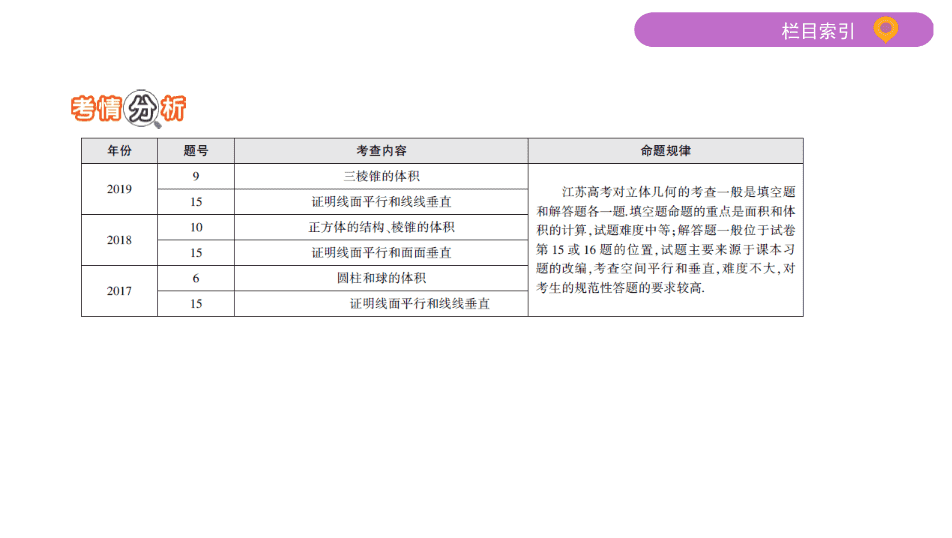
专题三 立体几何 第 8 讲　空间中的平行与垂直 第8讲　空间中的平行与垂直 1.(2019北京理,12,5分)已知 l , m 是平面 α 外的两条不同直线.给出下列三个论 断: ① l ⊥ m ;② m ∥ α ;③ l ⊥ α . 以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命 题: 　　　　　　　　     . 答案 　若 l ⊥ m , l ⊥ α ,则 m ∥ α (答案不唯一) 解析 　本题考查线面平行、垂直的位置关系,考查了逻辑推理能力和空间想 象能力. 把其中两个论断作为条件,余下的一个论断作为结论,共有三种情况.对三种 情况逐一验证.①②作为条件,③作为结论时,还可能 l ∥ α 或 l 与 α 斜交;①③作 为条件,②作为结论和②③作为条件,①作为结论时,容易证明命题成立. 2. α , β 为两个不同的平面, m , n 为两条不同的直线,下列命题中正确的是 　　          (填上所有正确命题的序号). ①若 α ∥ β , m ⊂ α ,则 m ∥ β ; ②若 m ∥ α , n ⊂ α ,则 m ∥ n ; ③若 α ⊥ β , α ∩ β = n , m ⊥ n ,则 m ⊥ β ; ④若 n ⊥ α , n ⊥ β , m ⊥ α ,则 m ⊥ β . 答案 　①④ 解析 　由面面平行的性质可得①正确;若 m ∥ α , n ⊂ α ,则 m , n 平行或异面,②错 误;由面面垂直的性质定理可知③中缺少条件“ m ⊂ α ”,错误;若 n ⊥ α , n ⊥ β ,则 α ∥ β ,又 m ⊥ α ,则 m ⊥ β ,④正确. 3.下列命题中,正确的序号是 　　　     . (1)平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平 行; (2)平行于同一个平面的两个平面平行; (3)若两个平面平行,则位于这两个平面内的直线互相平行; (4)若两个平面平行,则其中一个平面内的直线平行于另一个平面. 答案 　(1)(2)(4) 解析 　若两个平面平行,则位于这两个平面内的直线互相平行或异面,(3)错 误;由面面平行的判定和性质可得(1)(2)(4)都正确. 4.已知平面 α ⊥平面 β , α ∩ β = l ,直线 m ⊂ α ,直线 n ⊂ β ,且 m ⊥ n ,有以下四个结论:① 若 n ∥ l ,则 m ⊥ β ;②若 m ⊥ β ,则 n ∥ l ;③ m ⊥ β 和 n ⊥ α 同时成立;④ m ⊥ β 和 n ⊥ α 中 至少有一个成立.其中正确结论的序号是 　　　     . 答案 　①④ 解析 　若 n ∥ l ,则 m ⊥ l ,由面面垂直的性质定理可得 m ⊥ β ,①正确;若 m ⊥ β ,则 m ⊥ l ,又 m ⊥ n ,此时 n , l 的位置关系不确定,可能平行或相交,②错误; m ⊥ β 和 n ⊥ α 可能同时成立,也可能只有一个成立,③错误;④正确. 题型一　以锥体为载体的空间线面关系 例1     (2019南师大附中期中,16)如图,在四棱锥 P - ABCD 中, AP ⊥ CD , AD ∥ BC , AB = BC =1, AD =2, E , F 分别为 AD , PC 的中点.求证: (1) AP ∥平面 BEF ; (2)平面 BEF ⊥平面 PAC . 证明 　(1)设 AC 交 BE 于点 O ,连接 OF , CE .   因为 AE = BC =1, AD ∥ BC ,所以四边形 ABCE 为平行四边形, 所以点 O 为 AC 的中点, 又因为点 F 为 PC 的中点,所以 OF ∥ AP . 又因为 OF ⊂ 平面 BEF , AP ⊄ 平面 BEF ,所以 AP ∥平面 BEF . (2)因为 AD ∥ BC , ED = BC =1, 所以四边形 BCDE 为平行四边形,所以 BE ∥ CD . 因为 AP ⊥ CD ,所以 AP ⊥ BE . 又因为四边形 ABCE 为平行四边形, AB = BC , 所以四边形 ABCE 为菱形,所以 AC ⊥ BE . 又因为 AP ⊥ BE , AP ∩ AC = A , AP ⊂ 平面 APC , AC ⊂ 平面 APC , 所以 BE ⊥平面 APC . 因为 BE ⊂ 平面 BEF ,所以平面 BEF ⊥平面 PAC . 【方法归纳】　证明以锥体为载体的空间线面关系问题时,首先要考虑锥体 的几何特征,然后根据要证明的问题选择相应的判定定理或性质定理. 1-1     (2019苏锡常镇四市教学情况调查二,15)如图,在三棱锥 P - ABC 中,过点 P 作 PD ⊥ AB ,垂足为 D , E , F 分别是 PD , PC 的中点,且平面 PAB ⊥平面 PCD . 求证:(1) EF ∥平面 ABC ; (2) CE ⊥ AB . 证明 　(1)在三棱锥 P - ABC 中,因为 E , F 分别是 PD , PC 的中点,所以 EF 为△ PCD 的中位线, 则有 EF ∥ CD . 又 EF ⊄ 平面 ABC , CD ⊂ 平面 ABC , 所以 EF ∥平面 ABC . (2)因为平面 PAB ⊥平面 PCD ,平面 PAB ∩ 平面 PCD = PD , AB ⊥ PD , AB ⊂ 平面 PAB , 所以 AB ⊥平面 PCD , 又 CE ⊂ 平面 PCD ,所以 CE ⊥ AB . 题型二　以柱体为载体的空间线面关系 例2     (2019常州期末)如图,正三棱柱 ABC - A 1 B 1 C 1 中,点 M , N 分别是棱 AB , CC 1 的 中点. 求证:(1) CM ∥平面 AB 1 N ; (2)平面 A 1 BN ⊥平面 AA 1 B 1 B . 证明 　(1)设 AB 1 交 A 1 B 于点 O ,连接 OM , ON .   在正三棱柱 ABC - A 1 B 1 C 1 中, BB 1 ∥ CC 1 , BB 1 = CC 1 ,且四边形 AA 1 B 1 B 是平行四边形, 所以 O 为 AB 1 的中点, 又因为 M 为 AB 的中点,所以 OM ∥ BB 1 ,且 OM =   BB 1 . 因为 N 为 CC 1 的中点,所以 CN =   CC 1 ,所以 OM ∥ CN ,且 OM = CN . 所以四边形 CMON 是平行四边形. 所以 CM ∥ ON ,又 ON ⊂ 平面 AB 1 N , CM ⊄ 平面 AB 1 N , 所以 CM ∥平面 AB 1 N . (2)正三棱柱 ABC - A 1 B 1 C 1 中, BB 1 ⊥平面 ABC , 因为 CM ⊂ 平面 ABC ,所以 BB 1 ⊥ CM . 因为 CA = CB , M 为 AB 的中点,所以 CM ⊥ AB , 又由(1)知 CM ∥ ON ,所以 ON ⊥ AB , ON ⊥ BB 1 , 又因为 AB ∩ BB 1 = B , AB , BB 1 ⊂ 平面 AA 1 B 1 B , 所以 ON ⊥平面 AA 1 B 1 B . 又 ON ⊂ 平面 A 1 BN ,所以平面 A 1 BN ⊥平面 AA 1 B 1 B . 【方法归纳】　(1)面面垂直的证明依据是面面垂直的判定定理,即要证面面 垂直,则必须证明线面垂直,所以又要寻找线线垂直.(2)证明线面平行的方法 一般有两种:一是利用线面平行的判定定理,利用三角形中位线的性质或平行 四边形对边互相平行的性质寻找线线平行;二是先利用面面平行的判定定理 证明面面平行,再由面面平行的性质证明线面平行. 题型三　以不规则几何体为载体的空间线面关系 例3 　如图,在多面体 ABCDEF 中,四边形 ABCD 是菱形, AC , BD 相交于点 O , EF ∥ AB , AB =2 EF ,平面 BCF ⊥平面 ABCD , BF = CF ,点 G 为 BC 的中点. 求证:(1)直线 OG ∥平面 EFCD ; (2)直线 AC ⊥平面 ODE . 证明 　(1)∵四边形 ABCD 是菱形, AC ∩ BD = O , ∴点 O 是 BD 的中点. ∵点 G 是 BC 的中点,∴ OG ∥ CD ,且 OG =   CD . 又∵ OG ⊄ 平面 EFCD , CD ⊂ 平面 EFCD , ∴直线 OG ∥平面 EFCD . (2)∵ BF = CF ,点 G 为 BC 的中点,∴ FG ⊥ BC . ∵平面 BCF ⊥平面 ABCD ,平面 BCF ∩ 平面 ABCD = BC , FG ⊂ 平面 BCF , FG ⊥ BC , ∴ FG ⊥平面 ABCD . ∵ AC ⊂ 平面 ABCD ,∴ FG ⊥ AC . ∵ OG ∥ AB , OG =   AB , EF ∥ AB , EF =   AB , ∴ OG ∥ EF , OG = EF , ∴四边形 EFGO 为平行四边形,∴ FG ∥ EO . ∵ FG ⊥ AC ,∴ AC ⊥ EO . ∵四边形 ABCD 是菱形,∴ AC ⊥ DO . ∵ EO ∩ OD = O , EO , DO 在平面 ODE 内, ∴直线 AC ⊥平面 ODE . 【方法归纳】　证明或探究空间中线线、线面与面面平行或垂直的位置关 系时,(1)要熟练掌握所有判定定理与性质定理,梳理好常用的位置关系的证 明方法,如证明线面平行,既可以构造线线平行,也可以构造面面平行;(2)要掌 握解题时由已知想性质、由求证想判定,即综合法与分析法相结合来寻找证 明的思路.证题时要避免使用一些正确但不能作为推理依据的结论.此外,要 会分析一些非常规放置的空间几何体.