【数学】2020届一轮复习人教版（理）第7章第6讲空间向量及运算学案

【数学】2020届一轮复习人教版（理）第7章第6讲空间向量及运算学案

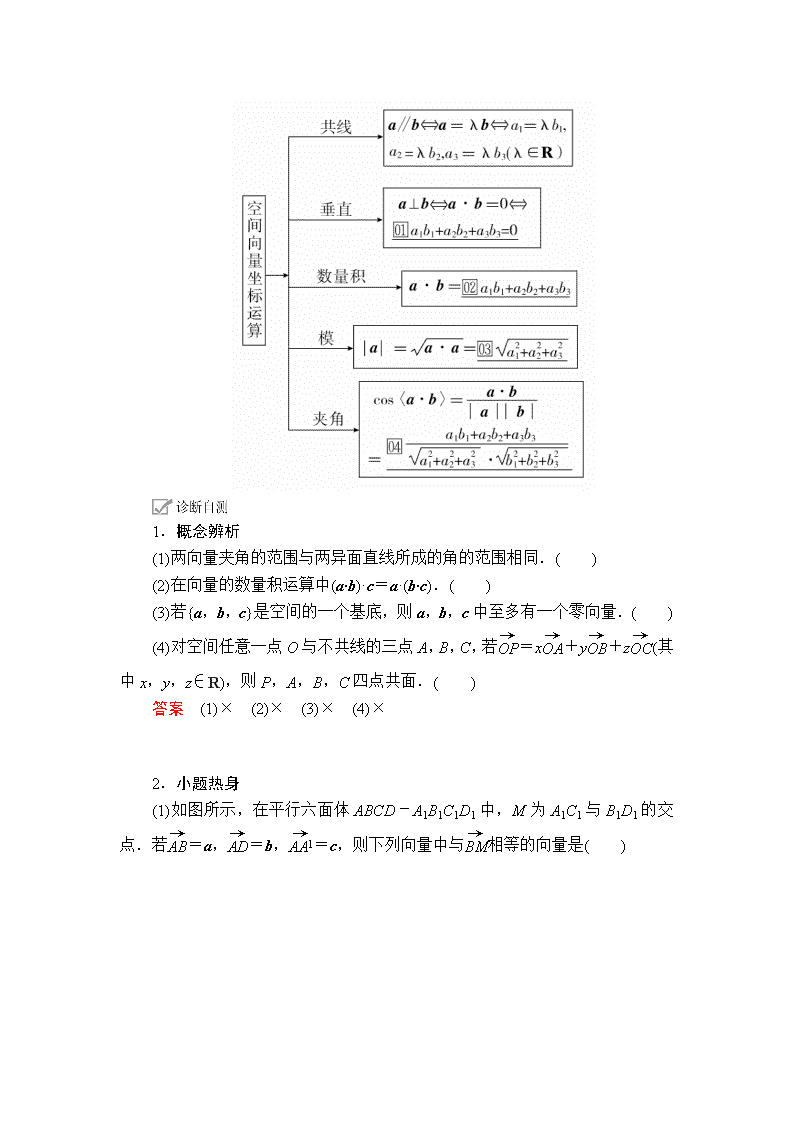
第6讲　空间向量及运算 ‎[考纲解读]　1.了解空间直角坐标系，会用空间直角坐标表示点的位置，了解空间向量的概念，了解空间向量的基本定理及其意义．‎ ‎2.能应用空间两点间的距离公式，掌握空间向量的正交分解及其坐标表示．‎ ‎3.掌握空间向量的线性运算及其坐标表示，掌握空间向量的数量积及其坐标表示，并能运用向量的数量积判断向量的共线与垂直．(重点、难点)‎ ‎[考向预测]　从近三年高考情况来看，本讲一直是空间立体几何的基础，一般不单独命题．预测2020年会与多面体相结合进行考查，题型为解答题，解题时利用空间向量法解决问题，试题难度不会太大，属中档题型.‎ ‎1．空间两点间的距离公式、中点公式 ‎(1)距离公式 ‎①设点A(x1，y1，z1)，B(x2，y2，z2)，‎ 则|AB|＝ .‎ ‎②设点P(x，y，z)，则与坐标原点O之间的距离为 ‎|OP|＝ .‎ ‎(2)中点公式 设点P(x，y，z)为P1(x1，y1，z1)，P2(x2，y2，z2)的中点，则.‎ ‎2．空间向量的数量积 a·b＝|a||b|cos〈a，b〉．‎ ‎3．空间向量的坐标运算 a＝(a1，a2，a3)，b＝(b1，b2，b3)(a，b均为非零向量)：‎ ‎1．概念辨析 ‎(1)两向量夹角的范围与两异面直线所成的角的范围相同．(　　)‎ ‎(2)在向量的数量积运算中(a·b)·c＝a·(b·c)．(　　)‎ ‎(3)若{a，b，c}是空间的一个基底，则a，b，c中至多有一个零向量．(　　)‎ ‎(4)对空间任意一点O与不共线的三点A，B，C，若＝x＋y＋z(其中x，y，z∈R)，则P，A，B，C四点共面．(　　)‎ 答案　(1)×　(2)×　(3)×　(4)×‎ ‎　 　　　　　　　　　　　　　　　　　　‎ ‎2．小题热身 ‎(1)如图所示，在平行六面体ABCD－A1B1C1D1中，M为A1C1与B1D1的交点．若＝a，＝b，＝c，则下列向量中与相等的向量是(　　)‎ A．－a＋b＋c B．a＋b＋c C．－a－b＋c D．a－b＋c 答案　A 解析　由题意，根据向量运算的几何运算法则，＝＋＝＋(－)＝c＋(b－a)＝－a＋b＋c.故选A.‎ ‎(2)若{a，b，c}为空间的一组基底，则下列各项中，能构成基底的一组向量是(　　)‎ A．a，a＋b，a－b B．b，a＋b，a－b C．c，a＋b，a－b D．a＋b，a－b，a＋2b 答案　C 解析　A，B，D中三组向量都是共面向量，不能构成基底，c，a＋b，a－b不共面可以构成基底．‎ ‎(3)已知向量a＝(2，－3,5)，b＝，且a∥b，则λ等于________．‎ 答案　－ 解析　因为a∥b，所以＝＝，所以λ＝－.‎ ‎(4)已知a＝(1,2，－2)，b＝(0,2,4)，则a，b夹角的余弦值为________．‎ 答案　－ 解析　cos〈a，b〉＝＝－.‎ 题型 　空间向量的线性运算 如图所示，在平行六面体ABCD－A1B1C1D1中，设＝a，＝b，＝c，M，N，P分别是AA1，BC，C1D1的中点，试用a，b，c表示以下各向量：‎ ‎(1)；‎ ‎(2)；‎ ‎(3)＋.‎ 解　(1)∵P是C1D1的中点，‎ ‎∴＝＋＋＝a＋＋＝a＋c＋＝a＋c＋b.‎ ‎(2)∵N是BC的中点，‎ ‎∴＝＋＋＝－a＋b＋＝－a＋b＋＝－a＋b＋c.‎ ‎(3)∵M是AA1的中点，‎ ‎∴＝＋＝＋＝－a＋a＋c＋b ‎＝a＋b＋c，‎ 又＝＋＝＋＝＋＝c＋a.‎ ‎∴＋＝＋＝a＋b＋c.‎ 条件探究　在举例说明条件下，若＝，＝2，试用a，b，c表示.‎ 解　如图，连接AF，则＝＋.‎ 由已知四边形ABCD是平行四边形，‎ 故＝＋＝b＋c，‎ ＝＋＝－a＋c.‎ 又＝－＝－(b＋c)，‎ 由已知＝2，‎ 所以＝＋＝－＝－ ‎＝c－(c－a)＝(a＋2c)，‎ 所以＝＋＝－(b＋c)＋(a＋2c)＝(a－b＋c)．‎ 用已知向量表示某一向量的注意事项 ‎(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．‎ ‎(2)要正确理解和运用向量加法、减法与数乘运算的几何意义．向量加法的多边形法则对空间向量仍然成立．‎ ‎(3)在立体几何中要灵活应用三角形法则，向量加法的平行四边形法则在空间仍然成立．‎ 提醒：灵活运用三角形法则或平行四边形法则，把所求向量用已知基向量表示出来．　 　　　　　　　　　　　　　　　　　　‎ ‎1．如图所示，在四面体OABC中，＝a，＝b，＝c，D为BC的中点，E为AD的中点，则＝________(用a，b，c表示)．‎ 答案　a＋b＋c 解析　因为D为BC的中点，‎ 所以＝(＋)＝(b＋c)，‎ 又因为E为AD的中点，所以＝(＋)＝＝a＋b＋c.‎ ‎2．如图所示，已知P为矩形ABCD所在平面外一点，PA⊥平面ABCD，点M在线段PC上，点N在线段PD上，且PM＝2MC，PN＝ND，若＝x＋y＋z，则x＋y＋z＝________.‎ 答案　－ 解析　＝－＝－＝(－)－(＋)＝－＋－(＋)＝－－＋，‎ 所以x＋y＋z＝－－＋＝－.‎ 题型 　共线向量与共面向量定理的应用 ‎1．(2018·郑州调研)已知a＝(2,1，－3)，b＝(－1,2,3)，c＝(7,6，λ)，若a，b，c三向量共面，则λ等于________．‎ 答案　－9‎ 解析　由题意知c＝xa＋yb，即(7,6，λ)＝x(2,1，－3)＋y(－1,2,3)，‎ ‎∴解得λ＝－9.‎ ‎2．(2018·唐山质检)如图所示，已知斜三棱柱ABC－A1B1C1，点M，N分别在AC1和BC上，且满足＝k，＝k(0≤k≤1)．‎ ‎(1)向量是否与向量，共面？‎ ‎(2)直线MN是否与平面ABB1A1平行？‎ 解　(1)∵＝k，＝k，‎ ‎∴＝＋＋ ‎＝k＋＋k ‎＝k(＋)＋ ‎＝k(＋)＋ ‎＝k＋＝－k ‎＝－k(＋)‎ ‎＝(1－k)－k，‎ ‎∴由共面向量定理知向量与向量，共面．‎ ‎(2)当k＝0时，点M，A重合，点N，B重合，MN在平面ABB1A1内，故直线MN与平面ABB1A1不平行．‎ 当00，则实数λ＝________.‎ 答案　3‎ 解析　因为λa＋b＝(4,1－λ，λ)，所以|λa＋b|＝＝，所以λ2－λ－6＝0(λ>0)，所以λ＝3.‎