福建莆田一中2012届高三数学上学期期末试卷 文 新人教A版
莆田一中2011-2012学年上学期期末试卷2012.1.
高三 数学(文科)
一、选择题:本大题共12个小题,每小题5分,共60分。
1.已知复数Z1=m+2i,Z2=3+4i,若Z1·Z2为实数,则实数m的值为( )
A. B. C.- D.-
2.设S={x||x-2|>3},T={x|a
-1
3.我市某学校在“9.11”举行老师、学生消防知识比赛,报名的学生和教师的人数之比为6:1,学校决定按分层抽样的方法从报名的师生中抽取35人组队进行比赛,已知教师甲被抽到的概率为,则报名的学生人数是( )
A.350 B.30 C.300 D.35
4.下列判断错误的是( )
A.“”是“a < b”的充分不必要条件
B.命题“”的否定是“ ”
C.若f (x)是定义在R上的奇函数,且f (x+2)也为奇函数,则f (x)是以4为周期的周期函数.
D.若为假命题, 则p, q均为假命题
5.中,,,,则( )
A.或 B. C. D.
6. 已知椭圆的焦点重合,则该椭圆的离心率是( )
A. B. C. D.
7. 是两条不同的直线,是两个不同的平面,则下列四个命题:
①若a⊥b,a⊥α,bα,则b∥α; ②若a∥α,a⊥β,则α⊥β;
③若a⊥β,α⊥β,则a∥α或aα; ④若a⊥b,a⊥α,b⊥β,则α⊥β.
其中正确命题的个数为( )
A.1 B.2 C.3 D.4
8. 直线有两个不同交点的一个充分不必要条件是 ( )
A. B. C. D.
9. 为奇函数,该函数的部分图像如图所示,、分别为最高点与最低点,并且,则该函数图象的一条对称轴为( )
A. B. C D.
10.实数满足不等式组,且 取 最小值的最优解有无穷多个, 则实数a的取值是( )
A. B. 1 C. 2 D. 无法确定
11.在等比数列中, ,使不等式 成立的最大自然数是( )
A.5 B.6 C.7 D.8
O
X
-1
Y
O
X
-1
Y
O
X
-1
Y
O
X
-1
Y
12.设函数,若为函数的一个极值点,则下列图像不可能为的图像是( )
A. B. C. D.
二、填空题:本大题共4个小题,每小题4分,共16分。
13. 曲线在点处的切线平行于直线,则点的坐标为 .
14.若函数,且,
则实数m的取值范围为 。
15.某三棱锥有五条棱的长度都为2,则当该三棱锥的表面积最大时其体积为 。
A
B
C
D
O
y
x
16.如图在平面直角坐标系中,圆()
内切于正方形,任取圆上一点,若
(、),则、满足的一个等式是______________________.
三.解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分共12分)
已知向量,,其中,且,又函数的图象与直线相切,相邻切点之间的距离为.
(Ⅰ)求的值;
(Ⅱ)设是第一象限角,且,求的值。
18.(本小题满分共12分)
如图,在底面为直角梯形的四棱锥中,,,,.
⑴求证:;
⑵当时,求此四棱锥的表面积.
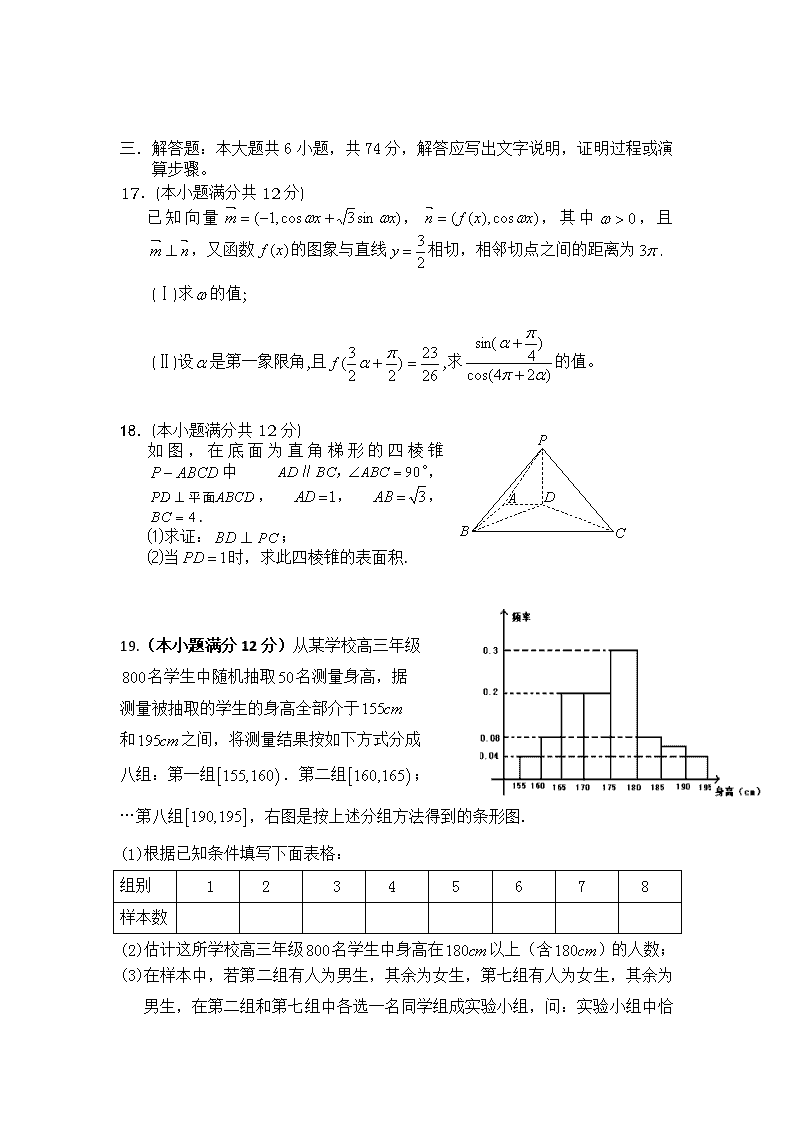
19.(本小题满分12分)从某学校高三年级
名学生中随机抽取名测量身高,据
测量被抽取的学生的身高全部介于
和之间,将测量结果按如下方式分成
八组:第一组.第二组;
…第八组,右图是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
组别
1
2
3
4
5
6
7
8
样本数
(2)估计这所学校高三年级名学生中身高在以上(含)的人数;
(3)在样本中,若第二组有人为男生,其余为女生,第七组有人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
20. (本小题满分12分)
数列{an}的前项和,数列{}满足。
(Ⅰ)求数列{},{}的通项公式;
(Ⅱ)若,为{}的前n 和,求。
21(本小题满分12分)
如图,已知椭圆:过点,上、下焦点分别为、,向量.直线与椭圆交于两点,线段中点为.
(1)求椭圆的方程;
(2)求直线的方程;
(3)记椭圆在直线下方的部分与线段所围成的平面区域(含边界)为,若曲线与区域有公共点,试求的最小值.
22.(本小题满分14分)
已知函数(其中常数), .
(Ⅰ)当时,若函数是奇函数,求的极值点;
(Ⅱ)若a0,求函数的单调递增区间;
(Ⅲ)当时,求函数在上的最小值,并探索:是否存在满足条件的实数,使得对任意的,恒成立.
班级 座号 姓名 准考证号
莆田一中2011—2012学年度上学期期末考试
高三文科数学 答题卷 2012.1.
二、填空题:
13. ; 14. ;
15. 16. .
三、解答题:
17. (本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22 、(本题满分14分)
莆田一中2011-2012学年上学期期末试卷2012.1
高三数学(文科)参考答案
1-5 DACDC 6-10 ADCDB 11-12 CD
13. 或 14. 15. 16.
17.解: (Ⅰ)由题意得,所以,
(4分)
函数的最小正周期为,又, (6分)
(Ⅱ)由(Ⅰ)知
所以
解得 (8分)
因为是第一象限角,故 (9分)
所以, (12分)
18 解:(1)证明:由题意知 则
(4分)
⑵
∴.
. (6分)
过D作DH⊥BC于点H,连结PH,则同理可证明,
并且.
(8分)
易得
.
. (11分)
故此四棱锥的表面积
(12分)
19. 解:(1)由条形图得第七组频率为∴第七组的人数为3人. (1分)
组别
1
2
3
4
5
6
7
8
样本数
2
4
10
10
15
4
3
2
(4分)
(2)由条形图得前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,后三组频率为1-0.82=0.18.估计这所学校高三年级身高在180cm以上(含180cm)的人数800×0.18=144(人). (8分)
(3)基本事件有12个,恰为一男一女的事件有共7个,因此实验小组中,恰为一男一女的概率是.(12分)
20.解:(1) (6分)
(Ⅱ)
(8分)
,两式相减得:
(12分)
21解:(1)
解得:,椭圆方程为 (4分)
(2)①当斜率不存在时,由于点不是线段的中点,所以不符合要求;
②设直线方程为,代入椭圆方程整理得
解得 所以直线 (8分)
(3)化简曲线方程得:,是以为圆心,为半径的圆。当圆与直线相切时,,此时为,圆心。
由于直线与椭圆交于,
故当圆过时,最小。此时,。 (12分)
22.解:(Ⅰ)因为函数是奇函数,对,成立,
得(利用奇函数,得也给1分)
得 (2分)
从得
经检验是函数的极值点 (4分)
(Ⅱ)因为 ,,
从,得
① ,方程的判别式,两根
单调递增区间为 (7分)
②时,单调递增区间为和(8分)
(Ⅲ) 因为,当时,令得,其中
当变化时,与的变化情况如下表:
函数在上的最小值为与的较小者
又,,
(10分)
由函数是奇函数,且,
时,,当时取得最大值
时,时,,
函数的最小值为, (1 2分)
要使对任意,恒成立,则
,
即不等式在上有解,符合上述不等式,
存在满足条件的实数,使对任意,恒成立, ( 14分)
(附:求的方法二如下)
当时,,
当变化时,与的变化情况如下表:
极小值
极大值
又时,