专题11-1 统计与概率的题型特点与命题规律-《奇招制胜》2017年高考数学（文）热点+题型全突破

专题11-1 统计与概率的题型特点与命题规律-《奇招制胜》2017年高考数学（文）热点+题型全突破

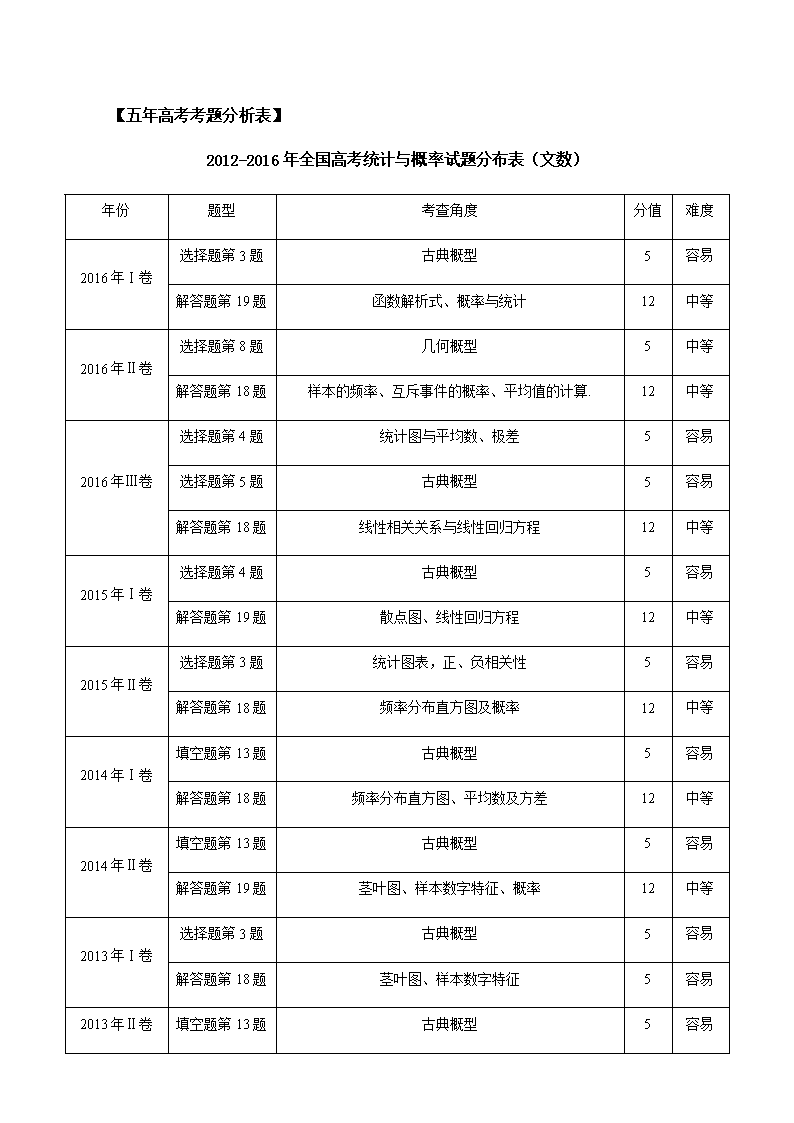
统计与概率的题型特点与命题规律 统计与概率是高考必考重点内容之一，文科高考考查的主要内容有：抽样方法、统计图表，统计数据的数字特征，变量间的相关关系、随机事件的概率、古典概型、几何概型，以及回归分析与独立性检验。‎ ‎【考纲解读】‎ 一、考点及要求 考试内容 要求层次 A B C 统计 随机抽样 简单随机抽样 ‎√‎ 分层抽样和系统抽样 ‎√‎ 用样本估计总体 频率分布表、直方图、折线图、茎叶图 ‎√‎ 样本数据的基本数字特征（如平均数、标准差）‎ ‎√‎ 用样本的频率分布表估计总体分步，用样本的基本数字特征估计总体的基本数字特征 ‎√‎ 变量的相关性 线性回归方程 ‎√‎ 统计案例 独立性检验 独立性检验（只要求2x2列联表）的基本思想、方法及其简单应用。‎ ‎√‎ 回归分析 回归分析的基本思想、方法及其简单应用。‎ ‎√‎ 概率 事件与概率 随机事件的概率 ‎√‎ 随机事件的运算 ‎√‎ 两个互斥事件的概率加法公式 ‎√‎ 古典概型 古典概型 ‎√‎ 几何概型 几何概型 ‎√‎ 说明: A.了解 B.理解 C.掌握 ‎【五年高考考题分析表】‎ ‎2012-2016年全国高考统计与概率试题分布表（文数）‎ 年份 题型 考查角度 分值 难度 ‎2016年Ⅰ卷 选择题第3题 古典概型 ‎5‎ 容易 解答题第19题 函数解析式、概率与统计 ‎12‎ 中等 ‎2016年Ⅱ卷 选择题第8题 几何概型 ‎5‎ 中等 解答题第18题 样本的频率、互斥事件的概率、平均值的计算.‎ ‎12‎ 中等 ‎2016年Ⅲ卷 选择题第4题 统计图与平均数、极差 ‎5‎ 容易 选择题第5题 古典概型 ‎5‎ 容易 解答题第18题 线性相关关系与线性回归方程 ‎12‎ 中等 ‎2015年Ⅰ卷 选择题第4题 古典概型 ‎5‎ 容易 解答题第19题 散点图、线性回归方程 ‎12‎ 中等 ‎2015年Ⅱ卷 选择题第3题 统计图表，正、负相关性 ‎5‎ 容易 解答题第18题 频率分布直方图及概率 ‎12‎ 中等 ‎2014年Ⅰ卷 填空题第13题 古典概型 ‎5‎ 容易 解答题第18题 频率分布直方图、平均数及方差 ‎12‎ 中等 ‎2014年Ⅱ卷 填空题第13题 古典概型 ‎5‎ 容易 解答题第19题 茎叶图、样本数字特征、概率 ‎12‎ 中等 ‎2013年Ⅰ卷 选择题第3题 古典概型 ‎5‎ 容易 解答题第18题 茎叶图、样本数字特征 ‎5‎ 容易 ‎2013年Ⅱ卷 填空题第13题 古典概型 ‎5‎ 容易 解答题第19题 频率分布直方图、函数、概率 ‎12‎ 中等 ‎2012年Ⅱ卷 选择题第3题 相关系数 ‎5‎ 中等 解答题第18题 函数、平均利润与概率 ‎12‎ 中等 ‎【高频考点展示】‎ ‎1.古典概型 ‎2.几何概型 ‎3.相关关系与线性回归方程 ‎4.茎叶图与样本数据特征及概率 ‎5.频率分布直方图与样本数据特征及概率 ‎6.函数与概率结合问题 ‎【命题预测】　‎ 通过研究近几年全国高考试卷，不难发现新课标对概率与统计模块的考查强调知识的应用性，考题为“一小一大”，即一道小题，一道大题，占17分，小题通常考查统计图的读取或概率计算，大题在解答题对统计和概率综合考查，难度不大。试题背景与日常生活贴近，联系也最为紧密，体现统计思想与概率思想，考查学生处理数据的能力，对概率事件的识别及概率的计算能力，以及考查学生的阅读与理解能力、分析问题与解决问题的能力．试题朝着“重基础、重能力、探究与创新”的方向发展．‎ ‎【典例1】【2016高考新课标3文（4）】某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图．图中点表示十月的平均最高气温约为，点表示四月的平均最低气温约为．下面叙述不正确的是（ ）‎ A.各月的平均最低气温都在以上 B.七月的平均温差比一月的平均温差大 C.三月和十一月的平均最高气温基本相同 D.平均气温高于的月份有5个 ‎【答案】D ‎【考点】1、平均数；2、统计图．‎ ‎【思路点拨】解答本题时易错可能有两种：（1）对图形中的线条认识不明确，找不到解决问题的方法；‎ ‎（2）估计平均温差时易出现错误. ‎ ‎【命题规律】‎ 试题的形式和难度都比较稳定，以给出统计图表，能够通过统计图表读出数据信息为常见形式.预计2017年的全国高考命题中，对统计图表的考查必有一道，命题的重点不变.‎ ‎【典例2】【2016高考新课标1文（3）】为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是（ ）‎ A． B. C. D.‎ ‎【答案】A 考点：古典概型 ‎【名师点睛】作为客观题形式出现的古典概型试题,一般难度不大,解答常见错误是在用列举法计数时出现重复或遗漏,避免此类错误发生的有效方法是按照一定的标准进行列举.‎ ‎【典例3】【2016高考新课标2文（8）‎ ‎】某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒.若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为（ ）‎ A. B. C. D. ‎【答案】B ‎【解析】：因为红灯持续时间为40秒.所以这名行人至少需要等待15秒才出现绿灯的概率为，故选B. ‎ 考点： 几何概型.‎ ‎【思路点拨】对于几何概型的概率公式中的“测度”要有正确的认识，它只与大小有关，而与形状和位置无关，在解题时，要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法．‎ ‎【命题规律】‎ 试题中对概率的考察为必考点，而近几年对几何概型的考察逐步成为热点，预计2017年的全国高考命题中，仍会考查，难度可能有所提高。‎ ‎【典例4】【2016高考新课标Ⅱ文（18）】某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 保费 随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：‎ 出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 频数 ‎60‎ ‎50‎ ‎30‎ ‎30‎ ‎20‎ ‎10‎ ‎（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；‎ ‎（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”.‎ 求的估计值；‎ ‎（III）求续保人本年度的平均保费估计值.‎ ‎【答案】（Ⅰ）=0.55； （Ⅱ）=0.3 （III）1.1925a.‎ ‎【解析】（Ⅰ）事件A发生当且仅当一年内出险次数小于2.由所给数据知，一年内险次数小于2的频率为；，故P(A)的估计值为0.55. ‎ ‎（Ⅱ）事件B发生当且仅当一年内出险次数大于1且小于4.由是给数据知，一年内出险次数大 于1且小于4的频率为，故P(B)的估计值为0.3.‎ 考点： 样本的频率、平均值的计算.‎ ‎【思路点拨】样本的数字特征常见的命题角度有：(1)样本的数字特征与直方图交汇；(2)样本的数字特征与茎叶图交汇；(3)样本的数字特征与优化决策问题.‎ ‎【命题规律】‎ 统计与概率的解答题难度比较稳定，通常为由日常生活情景中给出问题，然后通过读取统计图表的信息、求样本的数字特征，算概率等.预计2017年的全国高考命题中，解答题形式不变，但会朝着“重基础、重能力、探究与创新”的方向发展．‎