- 2021-07-01 发布 |
- 37.5 KB |
- 6页
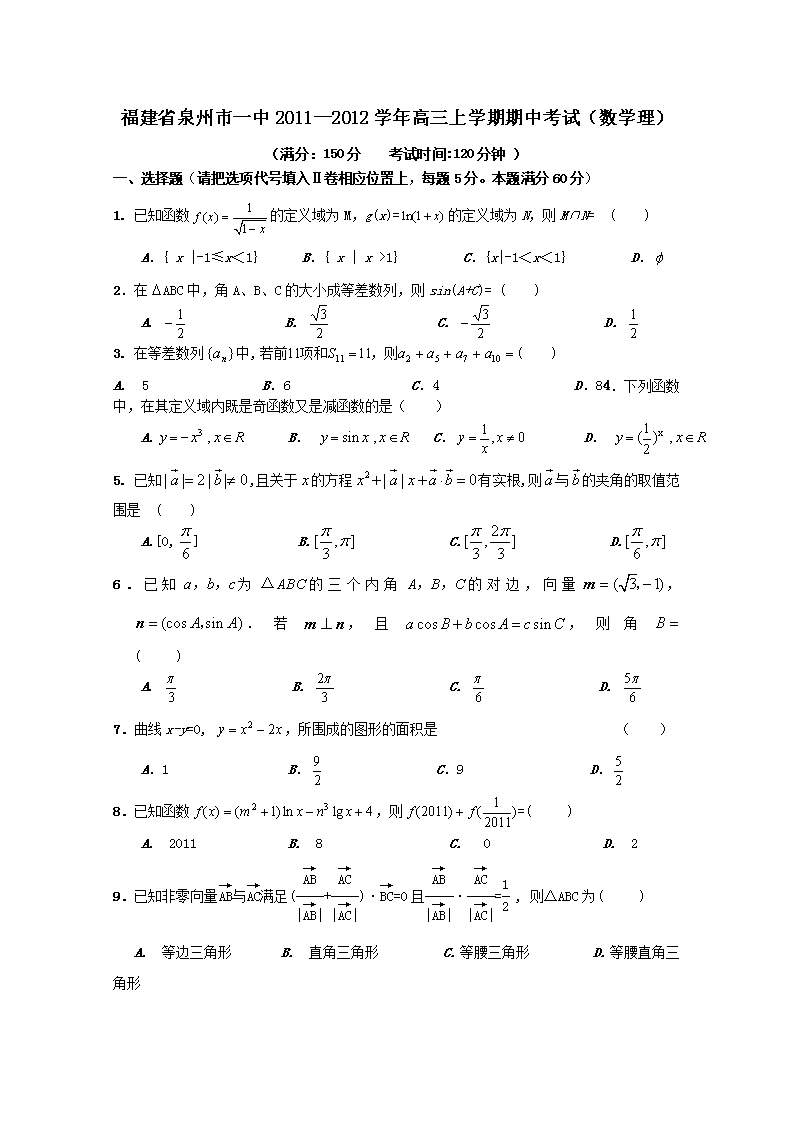


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
福建省泉州市一中2012届高三数学上学期期中考试 理 新人教A版
福建省泉州市一中2011—2012学年高三上学期期中考试(数学理) (满分:150分 考试时间:120分钟 ) 一、选择题(请把选项代号填入Ⅱ卷相应位置上,每题5分。本题满分60分) 1. 已知函数的定义域为M,g(x)=的定义域为N,则M∩N= ( ) A.{ x |-1≤x<1} B.{ x | x >1} C.{x|-1<x<1} D. 2.在ABC中,角A、B、C的大小成等差数列,则sin(A+C)= ( ) A. B. C. D. 3. 在等差数列中,( ) A. 5 B.6 C.4 D.84.下列函数中,在其定义域内既是奇函数又是减函数的是( ) A. B. C. D. 5. 已知,且关于的方程有实根,则与的夹角的取值范围是 ( ) A.[0,] B. C. D. 6.已知为的三个内角的对边,向量,.若,且,则角 ( ) A. B. C. D. 7.曲线x-y=0, ,所围成的图形的面积是 ( ) A.1 B. C.9 D. 8.已知函数,则=( ) A. 2011 B. 8 C. 0 D. 2 9.已知非零向量与满足(+)·=0且·= , 则△ABC为( ) A. 等边三角形 B. 直角三角形 C. 等腰三角形 D. 等腰直角三角形 10.已知向量,则= ( ) A.1 B. C.2 D. 11.已知各项均不为零的数列,定义向量,,. 下列命题中为真命题的是 ( ) A.若总有成立,则数列是等差数列 B.若总有成立,则数列是等比数列 C.若总有成立,则数列是等差数列 D.若总有成立,则数列是等比数列 12. f (x)是定义在(0,+∞)上的非负可导函数 ,且满足,若, ,则的大小关系是( )A. B. C. D. 二、填空题:(本大题共6小题,每小题6分,共36分)。 13. 已知是公比为的等比数列,且成等差数列,则_______ . 14.若是定义在上的奇函数,且,则 . 15. 若是偶函数,则有序实数对()可以是 . (写出你认为正确的一组数即可). 16. 给出下列四个命题: ① 集合A={-1,0,1},B={},则AB={1} ② 若函数,, 使; ③ 在△ABC中,若A>B,则sinA>sinB ; ④ 在数列中,,为非零常数.,且前项和为,则实数=-1; ⑤ 已知向量, ,, ,,; ⑥ 集合,若则的图象关于原点对称. 其中所有正确命题的序号是 . 泉州一中2011—2012学年度第一学期期中考试参考答案 高三数学(理科) 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B C A B C B B A A A B 二、填空题: 13. 1或 14. 0 15. (1,-1)(a+b=0)皆可 16. ①③④ 三、解答题:本大题共4题,共54分,解答应写出文字说明,证明过程或或演算步骤 y 2 -2 x o 17.(本小题满分12分) 函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<)的图象如图所示, (1)求y= f(x)的表达式; (2)若,求y=f(x)的值域。 解:(1)依题意得A=2, ……………………………… 2分 又ω=2 f(x)=2sin(2x+φ) ……………………………… 4分 把点(,2)带入上式得,2sin(+φ)=2,又|φ|<φ=……………………………… 6分 f(x)=2sin(2x+) ……………………………… 7分 (2)……………………………… 12分 18.(本小题满分12分) 在等比数列中,,公比, , 且4是与的等比中项,⑴求数列的通项公式; ⑵设,求数列的前项和, 解:(1)设等比数列的公比为q,则,由已知得 …………………………… 4分 解得 .…………………………… 7分 (2)由(1)知, …………………………… 12分 19. 在中,分别是角的对边,向量,,且 . (1) 求角的大小; (2) 设,且的最小正周期为,求在区间上的单调增区间及所有对称轴方程. 解:(1) …………………………… 5分 (2) ………… 7分 因为的最小正周期为,所以………… 8分 令 , 所以在区间上的单调增区间为…………………………… 10分 令, 所以在区间上的对称轴方程有…………………………… 12分 20.(本题满分12分) 设集合; (1)若,求的取值范围; (2)求函数的最值。 解:(1)…………………… 3分 …………………… 4分, 因为,所以…………………… 6分 (2)令t= …………………… 8分 …………………… 10分 当t=-3时,max=16, 当t= 时,min=-12 …………………… 12分 21.(本小题满分12分) 已知函数f(x)=xm+ax的导函数f′(x)=2x+1,,点An(n, Sn)在函数y=f(x) (n∈N*)的图像上 , (1)求证:数列为等差数列; (2)设,求数列的前项和 解:(1)由 f′(x)=2mx+a=2x+1得m=a=1,故f(x)=x2+x,…………………………… 2分 则依题意有 Sn= n2+n, 当n=1时,; …………… 3分 当n,…………… 4分 综上,,…………………………… 5分 故数列为等差数列…………………………… 6分 (2) =…………………………… 7分 ① 又 ②…………………………… 8分 ②-①: …………………………… 10分 …………………………… 12分 22.(本小题满分14分) 定义:若对定义域内的任意两个,均有成立,则称函数是上的“平缓函数”。 (1) 判断和的单调性并证明; (2) 判断和是否为R上的“平缓函数”,并说明理由; (3) 若数列中,总有。 查看更多