2021届课标版高考理科数学大一轮复习课件：9-2　直线、圆的位置关系（讲解部分）

2021届课标版高考理科数学大一轮复习课件：9-2　直线、圆的位置关系（讲解部分）

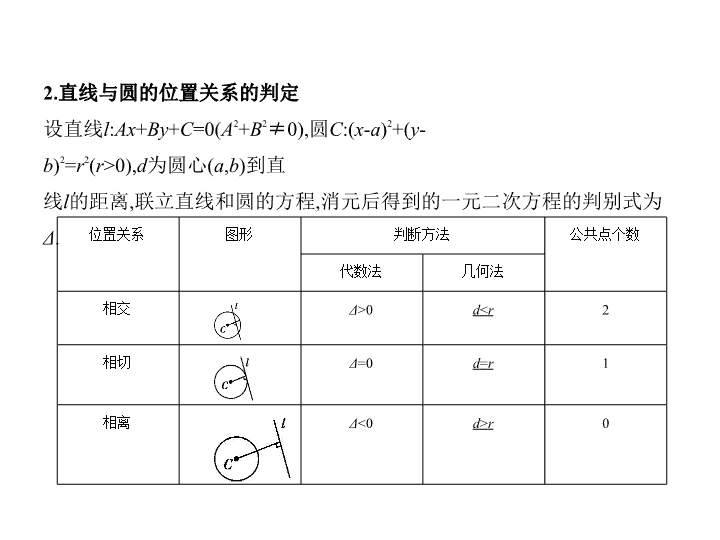
9.2 　直线、圆的位置关系 高考理数 考点一    直线与圆的位置关系 考点清单 考向基础 1.点与圆的位置关系 (1)根据点到圆心的距离 d 与圆的半径 r 的大小判断: d > r ⇔ 点在圆外; d = r ⇔ 点 在圆上; d < r ⇔ 点在圆内. (2)根据点 M ( x 0 , y 0 )与圆的方程( x - a ) 2 +( y - b ) 2 = r 2 的关系判断: ( x 0 - a ) 2 +( y 0 - b ) 2 > r 2 ⇔ 点在圆外; ( x 0 - a ) 2 +( y 0 - b ) 2 = r 2 ⇔ 点在圆上; ( x 0 - a ) 2 +( y 0 - b ) 2 < r 2 ⇔ 点在圆内. 2.直线与圆的位置关系的判定 设直线 l : Ax + By + C =0( A 2 + B 2 ≠ 0),圆 C :( x - a ) 2 +( y - b ) 2 = r 2 ( r >0), d 为圆心( a , b )到直 线 l 的距离,联立直线和圆的方程,消元后得到的一元二次方程的判别式为 Δ . 位置关系 图形 判断方法 公共点个数 代数法 几何法 相交   Δ >0 d < r 2 相切   Δ =0 d = r 1 相离   Δ <0 d > r 0 【温馨提示】 若一直线过圆内一点,则可判断此直线与圆相交.此法对过定点的动直线特 别有用. 3.与圆的切线有关的结论 (1)过圆 x 2 + y 2 = r 2 上一点 P ( x 0 , y 0 )的切线方程为 x 0 x + y 0 y = r 2 ; (2)过圆( x - a ) 2 +( y - b ) 2 = r 2 上一点 P ( x 0 , y 0 )的切线方程为( x 0 - a )( x - a )+( y 0 - b )( y - b )= r 2 ; (3)过圆 x 2 + y 2 = r 2 外一点 P ( x 0 , y 0 )作圆的两条切线,切点为 A , B ,则过 A 、 B 两点的 直线方程为 x 0 x + y 0 y = r 2 ; (4)过圆 x 2 + y 2 + Dx + Ey + F =0( D 2 + E 2 -4 F >0)外一点 P ( x 0 , y 0 )引圆的切线,切点为 T , 则切线长| PT |=   . 4.直线与圆相交 直线与圆相交时,若 l 为弦长, d 为弦心距, r 为半径,则有 r 2 = d 2 +   ,即 l =2   , 求弦长或已知弦长求其他量时,一般用此公式. 考向突破 考向    直线与圆的位置关系的判断 例　 直线 l : mx - y +1- m =0与圆 C : x 2 +( y -1) 2 =5的位置关系是   (　　) A.相交　　　　    B.相切　　   C.相离　　　　    D.不确定 解析 　解法一(代数法):由   消去 y ,整理得(1+ m 2 ) x 2 -2 m 2 x + m 2 -5=0, 因为 Δ =16 m 2 +20>0,所以直线 l 与圆相交. 解法二(几何法):由题意知,圆心(0,1)到直线 l 的距离 d =   <1<   ,故直 线 l 与圆相交. 解法三(点与圆的位置关系法):直线 l : mx - y +1- m =0过定点(1,1),因为点(1,1) 在圆 x 2 +( y -1) 2 =5的内部,所以直线 l 与圆相交. 答案     A 考点二    圆与圆的位置关系 考向基础 1.圆与圆的位置关系 设两圆的圆心距为 d ,两圆的半径分别为 R , r ( R > r ),则 位置关系 外离 外切 相交 内切 内含 图形           公共点个数 0 1 2 1 0 d , R , r 的关系 d > R + r d = R + r R - r < d < R + r d = R - r d < R - r 公切线条数 4 3 2 1 0 + F + λ ( Ax + By + C )=0( λ ∈R); (3)过圆 C 1 : x 2 + y 2 + D 1 x + E 1 y + F 1 =0和圆 C 2 : x 2 + y 2 + D 2 x + E 2 y + F 2 =0交点的圆系方程: x 2 + y 2 + D 1 x + E 1 y + F 1 + λ ( x 2 + y 2 + D 2 x + E 2 y + F 2 )=0( λ ≠ -1)(该圆系不含圆 C 2 ,解题时, 注意检验圆 C 2 是否满足题意,以防漏解). 2.两圆相交时,公共弦所在直线的方程 设圆 C 1 : x 2 + y 2 + D 1 x + E 1 y + F 1 =0①,圆 C 2 : x 2 + y 2 + D 2 x + E 2 y + F 2 =0②,若两圆相交,则 有一条公共弦,由①-②,得 ( D 1 - D 2 ) x +( E 1 - E 2 ) y + F 1 - F 2 =0 ③. 方程③表示圆 C 1 与 C 2 的 公共弦 所在直线的方程. 【知识拓展】    圆系方程 (1)同心圆系方程:( x - a ) 2 +( y - b ) 2 = r 2 ( r >0),其中 a , b 是定值, r 是参数; (2)过直线 Ax + By + C =0与圆 x 2 + y 2 + Dx + Ey + F =0交点的圆系方程: x 2 + y 2 + Dx + Ey 【知识拓展】     (1)当两圆相交时,两圆方程相减,所得的直线方程为两圆公共弦所在的直 线方程,这一结论的前提是两圆相交,如果不确定两圆是否相交,两圆方程 相减得到的方程不一定是两圆公共弦所在的直线方程. (2)两圆公共弦的垂直平分线过两圆的圆心. (3)求公共弦长时,几何法比代数法简单且易求. 考向突破 考向    由两圆位置关系求参数范围 例     已知点 A (-2,0), B (2,0),若圆( x -3) 2 + y 2 = r 2 ( r >0)上存在点 P (不同于点 A , B )使 得 PA ⊥ PB ,则实数 r 的取值范围是(　　) A.(1,5)　　　　    B.[1,5]　　　　    C.(1,3]　　　　    D.[3,5] 解析 　根据直径所对的圆周角为90 ° ,结合题意可得以 AB 为直径的圆和圆 ( x -3) 2 + y 2 = r 2 有交点, 显然两圆相切时不满足条件,故两圆相交. 易得以 AB 为直径的圆的方程为 x 2 + y 2 =4,又两个圆的圆心距为3,故| r -2|<3<| r +2|,得1< r <5,故选A. 答案     A 方法1      与圆有关的切线问题的处理方法 1.求过圆上一点( x 0 , y 0 )的切线方程的方法 若切线斜率存在且不为零,则先求切点和圆心连线的斜率 k ,由垂直关系知 切线斜率为-   ,由点斜式可求切线方程;若切线斜率不存在或为零,则可直 接写出切线的方程为 x = x 0 或 y = y 0 . 2.求过圆外一点( x 0 , y 0 )的圆的切线方程的方法 (1)几何法:当切线斜率存在时,设斜率为 k ,则切线方程为 y - y 0 = k ( x - x 0 ),即 kx - y + y 0 - kx 0 =0,由圆心到切线的距离等于半径列出关于 k 的方程,解方程即可得到 k 的值,从而可得切线方程;当切线斜率不存在时,可直接写出切线的方程为 x = x 0 . 方法技巧 (2)代数法:当切线斜率存在时,设斜率为 k ,则切线方程为 y - y 0 = k ( x - x 0 ),即 y = kx - kx 0 + y 0 ,代入圆的方程,得到一个关于 x 的一元二次方程,由 Δ =0求得 k 值,从而 得到切线方程;当切线斜率不存在时,可直接写出切线的方程为 x = x 0 . 例1     (2019广东七校联考,18)已知点 P (3,   +2), Q (4,3),圆 M :( x -1) 2 +( y -2) 2 =9. (1)求过点 P 的圆 M 的切线方程; (2)求过点 Q 的圆 M 的切线方程以及切线长. 解题导引 　(1)首先判断点 P 与圆 M 的位置关系,利用切线的性质求切线的 斜率,从而写出切线方程; (2)判断点 Q 与圆 M 的位置关系,从而对切线的斜率进行分类讨论,利用切线 的性质写出切线的方程,利用勾股定理写出切线长. 解析 　由题意知圆 M 的圆心为 M (1,2),半径 r =3. (1)∵(3-1) 2 +(   +2-2) 2 =9,∴点 P 在圆 M 上, 又 k PM =   =   , ∴切线的斜率 k =-   =-   . ∴过点 P 的圆 M 的切线方程为 y -(   +2)=-   ( x -3). 即2 x +   y -11-2   =0. (2)∵(4-1) 2 +(3-2) 2 =9+1=10>9, ∴点 Q 在圆 M 的外部. ①当过点 Q 的直线的斜率不存在时,直线的方程为 x =4,即 x -4=0, 又知点 M (1,2)到直线 x -4=0的距离 d =4-1=3= r , ∴直线 x -4=0符合题意. ②当过点 Q 的直线的斜率存在时,设直线方程为 y -3= k ( x -4),即 kx - y -4 k +3=0, 则圆心 M 到直线的距离 d =   =3. 即|1-3 k |=3   ,解得 k =-   , ∴切线方程为-   x - y -4 ×   +3=0,即4 x +3 y -25=0. 综上可知,过点 Q 的圆 M 的切线方程为 x =4或4 x +3 y -25=0. ∵| QM |=   =   , ∴过点 Q 的圆 M 的切线长为   =   =1. 方法2      与圆有关的弦长问题的处理方法 　　圆的弦长的求法:①几何法:设圆的半径为 r ,弦心距为 d ,弦长为 l ,则   = r 2 - d 2 ;②代数法:设弦所在直线 y = kx + b 与圆( x - a ) 2 +( y - b ) 2 = r 2 ( r >0)相交于 A ( x 1 , y 1 ), B ( x 2 , y 2 )两点,可列方程组   消去 y 后得到一个关于 x 的一元 二次方程,从而求得 x 1 + x 2 , x 1 x 2 ,则弦长| AB |=     . 例2     (2019豫北名校期中联考,19)已知以点 A (-1,2)为圆心的圆与直线 l 1 : x + 2 y +7=0相切,过点 B (-2,0)的动直线 l 与圆 A 相交于 M , N 两点, Q 是 MN 的中点. (1)求圆 A 的方程; (2)当| MN |=2   时,求直线 l 的方程. 解析 　(1)设圆 A 的半径为 r ,因为圆 A 与直线 l 1 : x +2 y +7=0相切, 所以 r =   =2   , 所以圆 A 的方程为( x +1) 2 +( y -2) 2 =20. (2)当直线 l 垂直于 x 轴时,直线 l 的方程为 x =-2, 将 x =-2代入圆 A 的方程,得(-2+1) 2 +( y -2) 2 =20,解得 y =2 ±   , 此时| MN |=2   ,则 x =-2符合题意. 当直线 l 与 x 轴不垂直时,设直线 l 的斜率为 k , 则直线 l 的方程为 y = k ( x +2),即 kx - y +2 k =0. 因为 Q 是 MN 的中点,连接 AQ ,所以 AQ ⊥ MN , 所以| AQ | 2 +   = r 2 , 又知| MN |=2   , r =2   , 所以| AQ |=   =1. 即   =1,∴( k -2) 2 = k 2 +1. 解得 k =   . 所以直线 l 的方程为 y =   ( x +2),即3 x -4 y +6=0. 综上,满足题意的直线 l 的方程为 x =-2或3 x -4 y +6=0.