数学理卷·2017届北京市丰台区高三3月综合练习（一）（2017

数学理卷·2017届北京市丰台区高三3月综合练习（一）（2017

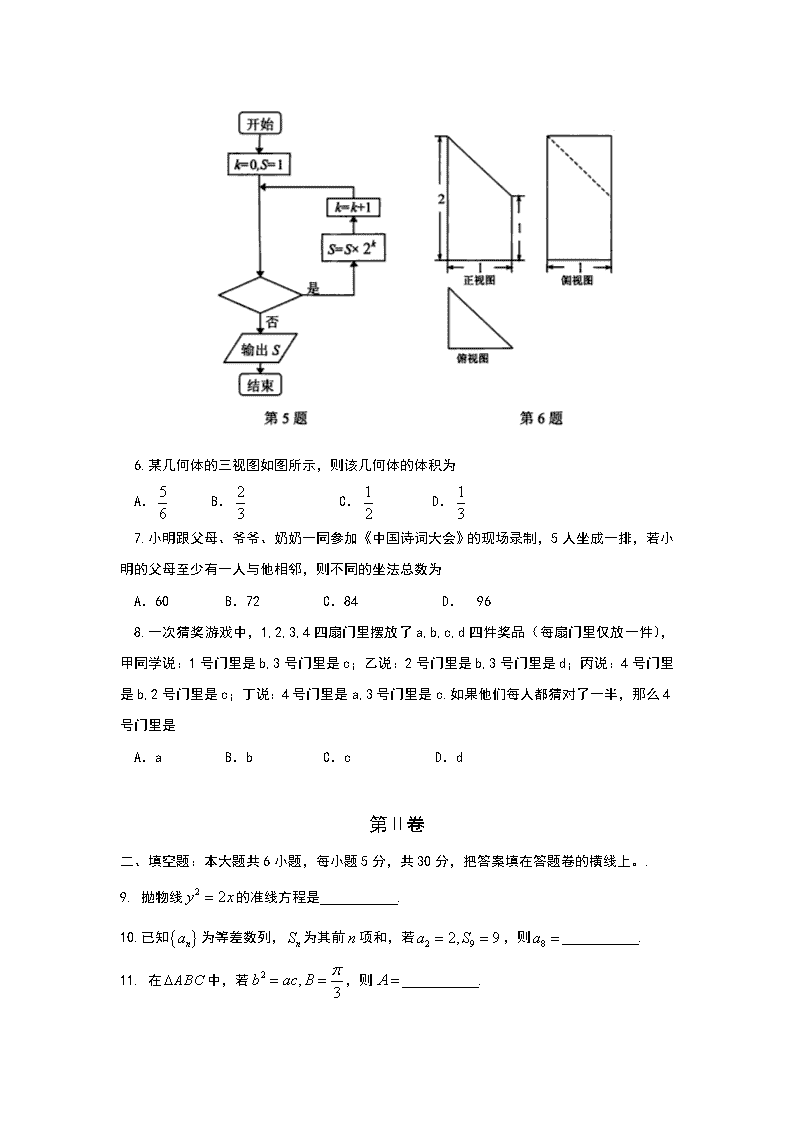
丰台区2017年高三年级第二学期综合练习（一）‎ 数学（理科）‎ 第Ⅰ卷 一、选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.如果集合，那么 A． B． C． D．‎ ‎2.已知，则“”是“复数是纯虚数”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎3.定积分 A． B． C． D． ‎ ‎4.设E,F分别是正方形ABCD的边AB,BC上的点，且，如果（为实数），那么的值为 A． B．0 C． D．1‎ ‎5.执行如图所示的程序框图，若输出的的值为64，则判断框内应填入的条件是 A． B． C． D ．‎ ‎6.某几何体的三视图如图所示，则该几何体的体积为 A． B． C． D．‎ ‎7.小明跟父母、爷爷、奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排，若小明的父母至少有一人与他相邻，则不同的坐法总数为 A．60 B．72 C．84 D． 96‎ ‎8.一次猜奖游戏中，1,2,3,4四扇门里摆放了a,b,c,d四件奖品（每扇门里仅放一件），甲同学说：1号门里是b,3号门里是c；乙说：2号门里是b,3号门里是d；丙说：4号门里是b,2号门里是c；丁说：4号门里是a,3号门里是c.如果他们每人都猜对了一半，那么4号门里是 A．a B．b C．c D．d 第Ⅱ卷 二、填空题：本大题共6小题，每小题5分，共30分，把答案填在答题卷的横线上。.‎ ‎9. 抛物线的准线方程是 .‎ ‎10.已知为等差数列，为其前项和，若，则 .‎ ‎11. 在中，若，则 .‎ ‎12. 若满足，则的取值范围是 .‎ ‎13.在平面直角坐标系中，曲线，曲线（为参数），过原点O的直线分别交于A,B两点，则的最大值是 .‎ ‎14．已知函数，下列命题正确的是 .（写出所有正确的命题编号）‎ ‎①是奇函数；‎ ‎②是R上的单调递增函数；‎ ‎③方程有且仅有1个实数根；‎ ‎④如果对任意，都有，那么的最大值为2.‎ 三、解答题：本大题共6小题，满分80分，解答应写出文字说明、证明过程或演算步骤 ‎15、（本小题满分13分）‎ ‎ 已知函数的图象如图所示.‎ ‎（1）求的解析式；‎ ‎ （2）若，求在上的单调递减区间.‎ ‎16、（本小题满分14分）‎ ‎ 如图1，平面五边形ABCDE中，是边长为2的正三角形，现将沿折起，得到四棱锥（如图2），且 ‎（1）求证：平面平面；‎ ‎ （2）求平面和平面所成锐二面角的大小；‎ ‎（3）在棱上是否存在点F，使得平面？若存在，求的值；若不存在，请说明理由.‎ ‎17、（本小题满分13分）‎ 某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了了解三种品牌的口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试他们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：‎ ‎（1）已知该公司购买的C品牌电动智能送风口罩比B品牌多200台，求该公司购买的B品牌电动智能送风口罩的数量；‎ ‎ （2）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A品牌待机时长高于B品牌的概率；‎ ‎（3）再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a,b,c（单位：小时）.这3个数据与表格中的数据构成的新样本平均数为 ‎，表格中数据的平均数为，写出的最小值（结果不要求证明）.‎ ‎18、（本小题满分13分）已知函数 ‎（1）求的单调区间；‎ ‎ （2）对任意的都有，求的取值范围.‎ ‎19、（本小题满分14分）已知椭圆的离心率为，右焦点为F，点在椭圆上 ‎（1）求椭圆的方程；‎ ‎ （2）过点F的直线交椭圆于M,N两点，交直线于点P，设，求证:为定值.‎ ‎20、（本小题满分13分）‎ 对于，若数列满足，则称这个数列为“K数列”.‎ ‎（1）已知数列是“K数列”，求实数的取值范围；‎ ‎ （2）是否存在首项为-1的等差数列为“K数列”，且其前项和满足？若存在，求出的通项公式；若不存在，请说明理由.‎ ‎（3）已知各项均为正整数的等比数列是“K数列”，数列不是“K数列”，若，试判断数列是否为“K数列”，并说明理由.‎