- 2021-07-01 发布 |
- 37.5 KB |
- 7页


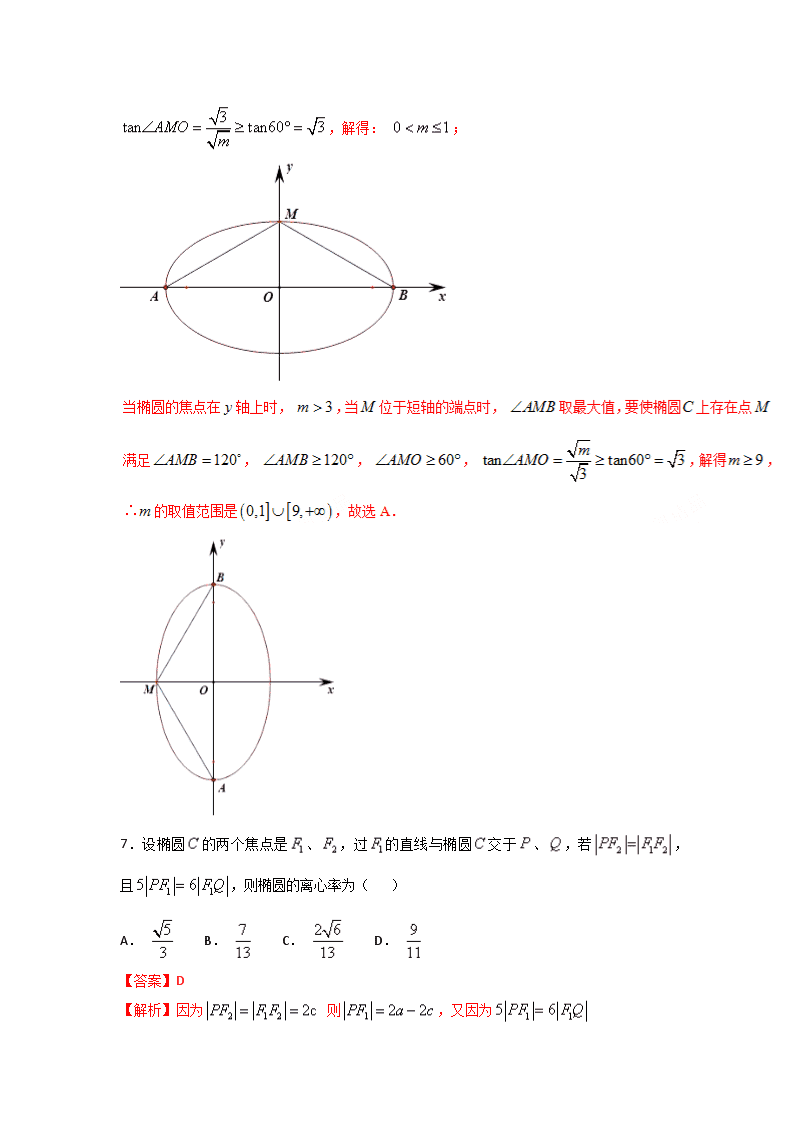
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题15 圆锥曲线(第02期)-2018年高考数学(理)备考之百强校小题精练系列
2018届高考数学(理)小题精练 专题15 圆锥曲线 1.若双曲线以椭圆的焦点为顶点,以椭圆长轴的端点为焦点,则双曲线的方程为( ) A. B. C. D. 【答案】B 2.已知为双曲线的一个焦点,则点到的一条渐近线的距离为( ) A. 2 B. 4 C. D. 【答案】A 【解析】双曲线,双曲线焦点到一条渐近线的距离为虚轴长的一半. 故选A. 3.P是双曲线上的点,是其焦点,且,若的面积是9,,则双曲线的离心率为( ) A. B. C. D. 【答案】D 【解析】设,由题意得, ,且的面积是, ,得中,根据勾股定理得, , ,结合双曲线定义,得, ,化简整理得, ,即,可得,结合,得, 该双曲线的离心率为,故选D. 4.直线 与双曲线交于不同的两点,则斜率的取值范围是( ) A. B. C. D. 【答案】C 5.若点O和点F分别为椭圆的中心和左焦点,点P为椭圆上的任意一点,则的最大值为( ) A. 6 B. 3 C. 2 D. 8 【答案】B 【解析】设P(x,y),F(-1,0) 则=(x,y)•(x+1,y)=x2+x+y2, 又点P在椭圆上,所以x2+x+y2=x2+x+(3﹣x2)=x2+x+3=(x+2)2+2, 又﹣2≤x≤2, 所以当x=2时,(x+2)2+2取得最大值为6,即的最大值为6, 故选:A. 点睛:本题利用代数方法处理数量积问题,借助点在椭圆上把两元问题转化为一元问题,配方后,利用二次函数的图象与性质即可得到的最大值. 6.设是椭圆长轴的两个端点,若上存在点满足,则的取值范围是( ) A. B. C. D. 【答案】A 【解析】当椭圆的焦点在轴上,即时,当位于短轴的端点时, 取最大值,要使椭圆上存在点满足, , , ,解得: ; 7.设椭圆的两个焦点是、,过的直线与椭圆交于、,若,且,则椭圆的离心率为( ) A. B. C. D. 【答案】D 【解析】因为 则,又因为 则 即,解得 故选D 点睛:运用椭圆的定义结合题目条件可以求得各线段的表达式,在和中利用余弦定理,建立的数量关系,求解关于的方程即可,计算量较大。 8.已知直线: 过椭圆的上顶点和左焦点,且被圆截得的弦长为,若,则椭圆离心率的取值范围是( ) A. B. C. D. 【答案】A 9.已知过点的直线与圆相交于、两点,若,则点的轨迹方程是( ) A. B. C. D. 【答案】B 【解析】设, ,过点的直线为, 由得,直线代入得 则, 即, ,所以,故选B 10.如图,已知抛物线的焦点为,直线过且依次交抛物线及圆于点四点,则的最小值为( ) A. B. C. D. 【答案】B 【解析】 【方法点睛】本题主要考查抛物线的定义和几何性质,以及基本不等式求最值,属于难题. 与焦点、准线有关的问题一般情况下都与拋物线的定义有关,解决这类问题一定要注意点到点的距离与点到直线的距离的转化:(1)将抛线上的点到准线距转化为该点到焦点的距离;(2)将抛物线上的点到焦点的距离转化为到准线的距离,本题就是将转化为到准线的距离后,再利用韦达定理与基本不等式使问题得到解决的. 11.已知直线 被椭圆截得的弦长为2017,则下列直线中被椭圆截得的弦长一定为2017的有( ) ① ② ③ ④ A. 1条 B. 2条 C. 3条 D. 4条 【答案】C 12.、分别是椭圆的左顶点和上顶点, 是该椭圆上的动点,则点到 直线 的距离的最大值为( ) A. B. C. D. 【答案】D 【解析】由椭圆方程可得,可得方程为,即,设,则点到直线 的距离为 ,故选D. 【方法点晴】本题主要考查椭圆的方程与性质及利用三角函数求最值,属于难题. 求与三角函数有关的最值常用方法有以下几种:①化成的形式利用配方法求最值;②形如的可化为的形式利用三角函数有界性求最值;③型,可化为求最值 .本题是利用方法③的思路解答的.查看更多