2020届二轮复习正弦、余弦定理及解三角形基础学案（全国通用）

2020届二轮复习正弦、余弦定理及解三角形基础学案（全国通用）

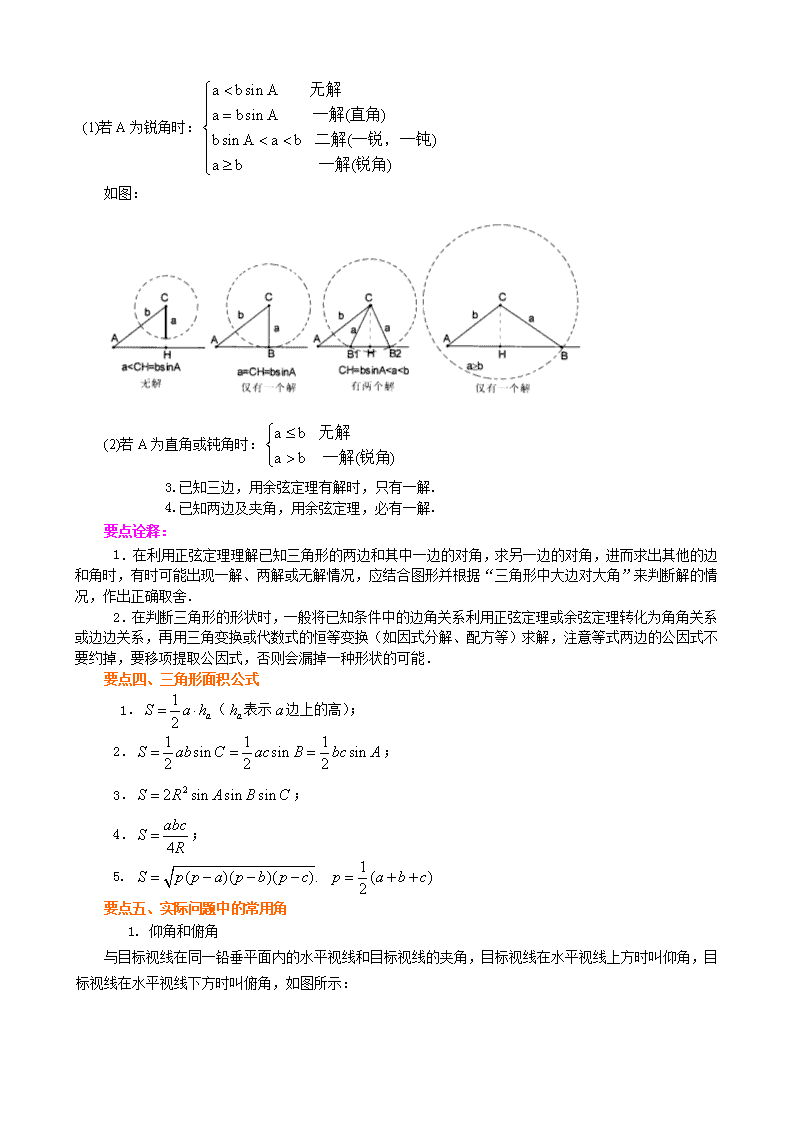
正弦、余弦定理及解三角形 ‎ ‎ ‎【考纲要求】‎ ‎1、掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.‎ ‎2、能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.‎ ‎【知识网络】‎ 应用 解三角形 正弦定理 余弦定理 ‎【考点梳理】‎ 要点一、三角形中的边与角之间的关系 约定：的三个内角、、所对应的三边分别为、、.‎ ‎1．边的关系：‎ ‎(1) 两边之和大于第三边：，，；‎ 两边之差小于第三边：，，；‎ ‎(2) 勾股定理：中，.‎ ‎2．角的关系：‎ ‎　中，,=‎ ‎（1）互补关系：‎ ‎（2）互余关系：‎ ‎3．直角三角形中的边与角之间的关系 中，（如图），有：‎ ‎，‎ ‎.‎ 要点二、正弦定理、余弦定理 ‎1.正弦定理：在—个三角形中，各边和它所对角的正弦的比相等．即：‎ ‎　　（为的外接圆半径）‎ ‎2. 余弦定理：三角形任意一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。即：‎ ‎ ‎ 要点诠释：‎ ‎（1）正弦定理适合于任何三角形；每个等式可视为一个方程：知三求一.‎ ‎（2）利用正弦定理可以解决下列两类三角形的问题：‎ ‎ ①已知两个角及任意—边，求其他两边和另一角；‎ ‎ ②已知两边和其中—边的对角，求其他两个角及另一边.‎ ‎（3）利用余弦定理可以解决下列两类三角形的问题：‎ ‎①已知三角形的两条边及夹角，求第三条边及其他两个角；‎ ‎②已知三角形的三条边，求其三个角.‎ ‎(4) 利用余弦定理判断三角形形状：‎ ‎①勾股定理是余弦定理的特殊情况，.‎ ‎②在中，，所以为锐角；‎ 若，，同理可得角、为锐角.‎ 当，，都成立时，为锐角三角形．‎ ‎③在中，若，‎ 所以为钝角，则是钝角三角形．‎ 同理：若，则是钝角三角形且为钝角；‎ ‎ 若，则是钝角三角形且为钝角．‎ 要点三、解斜三角形的类型 ‎1.已知两角一边，用正弦定理，有解时，只有一解.‎ ‎2.已知两边及其一边的对角，用正弦定理，有解的情况可分为以下情况，在中，已知和角时，解的情况如下：‎ ‎ (1)若A为锐角时：‎ 如图：‎ ‎(2)若A为直角或钝角时：‎ ‎3.已知三边，用余弦定理有解时，只有一解.‎ ‎4.已知两边及夹角，用余弦定理，必有一解.‎ 要点诠释：‎ ‎1．在利用正弦定理理解已知三角形的两边和其中一边的对角，求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解或无解情况，应结合图形并根据“三角形中大边对大角”来判断解的情况，作出正确取舍.‎ ‎2．在判断三角形的形状时，一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角角关系或边边关系，再用三角变换或代数式的恒等变换（如因式分解、配方等）求解，注意等式两边的公因式不要约掉，要移项提取公因式，否则会漏掉一种形状的可能．‎ 要点四、三角形面积公式 ‎ 1．（表示边上的高）；‎ ‎2．；‎ ‎3．；‎ ‎4．；‎ ‎5. ‎ 要点五、实际问题中的常用角 ‎1. 仰角和俯角 与目标视线在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方时叫仰角，目标视线在水平视线下方时叫俯角，如图所示：‎ ‎2.方位角：一般指正北方向线顺时针到目标方向线的水平角. 方位角的取值范围为0°～360°.‎ 如图，点的方位角是。‎ ‎3. 坡角和坡度 坡面与地平面所成的角度，叫做坡角；坡面的铅直高度和水平宽度的比叫做坡度或者坡比，常用字母i表示。坡比是坡角的正切值。‎ ‎【典型例题】‎ 类型一、利用正弦、余弦定理解三角形 例1. 在中，已知下列条件，解三角形.‎ ‎（1）, , ； ‎ ‎（2），，.‎ ‎【思路点拨】画出示意图（1）正弦定理的运用；（2）余弦定理的运用.‎ ‎【解析】‎ ‎（1）∵， ‎ 法一：∵， ∴或，‎ ‎①当时，，；‎ ‎②当时，（舍去）.‎ 法二：∵，∴，即， ‎ ‎∴，，.‎ ‎（2）∵‎ ‎∴‎ 法一：∵ ‎ ‎∴，‎ 法二：∵‎ 又∵，即 ‎∴，有，‎ ‎∴，.‎ ‎【总结升华】‎ ‎①解三角形时，可以依据题意画出恰当的示意图，然后正确选择正、余弦定理解答；‎ ‎②解三角形时，要留意三角形内角和为180°，同一个三角形中大边对大角等性质的应用.‎ 举一反三：‎ ‎【变式1】在△ABC中，a＝，b＝，B＝45°.求角A，C和边c.‎ ‎【解析】由正弦定理得，，‎ ‎∴sin A＝.∵a＞b，∴A＝60°或A＝120°.‎ 当A＝60°时，C＝180°－45°－60°＝75°，c＝；‎ 当A＝120°时，C＝180°－45°－120°＝15°，c＝.‎ ‎【变式2】在△ABC中，A＝60°，B＝75°，a＝10，则c等于( )．‎ A． B． ‎ C. D．‎ ‎【答案】C ‎【解析】由A＋B＋C＝180°，知C＝45°，‎ 由正弦定理得：，即∴c＝.‎ 正、余弦定理及解三角形401223 例1】‎ ‎【变式3】 在△ABC中，AB＝2，AC＝3，，则BC＝(　　)‎ A. B. C． D. ‎ ‎【答案】A ‎【解析】∵， ∴,‎ ‎∴，‎ 由余弦定理有 ‎∴，从而BC＝.‎ 例2. 在△ABC中，已知，试判断△ABC的形状．‎ ‎【思路点拨】将等式左边正切化为正弦、余弦形式，右边运用正弦定理将边化为角的形式，化简再判断.也可以直接将等式左边化为边的形式判断.‎ ‎【解析】方法一：化边为角 由题意得 ，化简整理得sinAcosA=sinBcosB即sin2A=sin2B ‎∴2A=2B或2A+2B=π ∴A=B或，‎ ‎∴三角形的形状为等腰三角形或直角三角形．‎ 方法二：化角为边 由已知得结合正、余弦定理得，‎ 整理得 ∴ ‎ 即三角形为等腰三角形或直角三角形 ‎【总结升华】依据正、余弦定理定理的结构特点，若在式子中出现的为与边相关的一次式，则一般多用正弦定理，；若在式子中出现的为与边相关的二次式，则一般多用余弦定理.‎ 举一反三：‎ ‎【变式1】在△ABC中，若2cosBsinA=sinC，则△ABC的形状一定是（ ）‎ A．等腰直角三角形 B．等腰三角形 C．直角三角形 D．等边三角形 ‎【答案】B ‎【解析】解法一：由已知结合正、余弦定理得 ‎，整理得a2=b2，∴a=b，∴△ABC一定是等腰三角形.‎ 解法二：∵，‎ ‎∴由已知得sinAcosB―cosAsinB=0，即sin（A―B）=0。‎ 又A―B∈（－π，π），∴A－B=0，即A=B，∴△ABC为等腰三角形.‎ ‎【变式2】在中，若b=asinC,c=acosB，试判断的形状．‎ ‎【答案】为等腰直角三角形 ‎【解析】由b=asinC可知 ，‎ 由c=acosB可知整理得，即三角形一定是直角三角形，∠A=，∴sinC=sinB∴∠B=∠C，∴△ABC为等腰直角三角形．‎ 类型二、解三角形及其综合应用 例3.（2017 山东高考）在△ABC中，角A，B，C的对边分别为a，b，c，已知 ‎（Ⅰ）证明：a+b=2c;‎ ‎（Ⅱ）求cosC的最小值.‎ ‎【思路点拨】（Ⅰ）把已知公式利用切化弦公式化简，再使用两角和差公式后用正弦定理即可；（Ⅱ）根据Ⅰ，利用余弦定理及基本不等式即可。‎ ‎【解析】(Ⅰ)由题意知,‎ 化简得2(sinAcosB+sinBcosA)=sinA+sinB,‎ 即2sin(A+B)= sinA+sinB,‎ 因为A+B+C=π,‎ 所以sin(A+B)=sin（π-C）=sinC，‎ 从而sinA+sinB=2sinC.‎ 由正弦定理得a+b=2c.‎ ‎（Ⅱ）由Ⅰ知，‎ 所以 当且仅当a=b时，等号成立.‎ 所以的最小值为．‎ ‎【总结升华】有关三角形中的三角函数问题，灵活运用正弦、余弦定理把边、角之间的关系相互转化，从而达到解题的目的.‎ 举一反三：‎ ‎【变式1】（2018 湖南高考）设△ABC的内角A，B，C的对边分别为a，b，c，a=btanA．‎ ‎（Ⅰ）证明：sinB=cosA；‎ ‎（Ⅱ）若sinC﹣sinAcosB=，且B为钝角，求A，B，C．‎ ‎【解析】（Ⅰ）证明：∵a=btanA．‎ ‎∴=tanA，‎ ‎∵由正弦定理：，又tanA=，‎ ‎∴=，‎ ‎∵sinA≠0，‎ ‎∴sinB=cosA．得证．‎ ‎（Ⅱ）∵sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB，‎ ‎∴sinC-sinAcosB=cosAsinB=，由（1）sinB=cosA，‎ ‎∴sin2B=，‎ ‎∵0＜B＜π，‎ ‎∴sinB=，‎ ‎∵B为钝角，‎ ‎∴B=，‎ 又∵cosA=sinB=，‎ ‎∴A=，‎ ‎∴C=π﹣A﹣B=，‎ 综上，A=C=，B=．‎ 正、余弦定理及解三角形401223 例4】‎ ‎【变式2】在△ABC中,角A、B、C所对的边分别为a,b,c，已知 ‎ (I)求sinC的值；‎ ‎(Ⅱ)当a=2， 2sinA=sinC时，求b及c的长．‎ ‎【答案】(I) (Ⅱ) ‎ 例4. 如图，A，B是海面上位于东西方向相距海里的两个观测点. 现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距 海里的C点的救援船立即前往营救，其航行速度为30海里／小时，该救援船到达D点需要多少时间？‎ ‎【思路点拨】在△DAB中，由正弦定理得，由此可求得；然后在△DAB中，由余弦定理可求得CD；最后根据时间=路程速度，即可求得该救援船到达D点需要的时间. 准确找出题目中的方向角是解题的关键之处.‎ ‎【解析】由题意知（海里），‎ ‎∠DBA=90°－60°=30°，∠DAB=90°－45°=45°，‎ ‎∴∠ADB=180°－(45°+30°)=105°，‎ 在△DAB中，由正弦定理得，‎ ‎∴‎ ‎（海里）.‎ 又∠DBC=∠DBA+∠ABC=30°+(90°－60°)=60°，海里，在△DBC中，由余弦定理得 ‎，‎ ‎∴CD=30（海里），则需要的时间（小时）.‎ ‎【总结升华】对图形进行有效的分析，便于使用正弦、余弦定理.‎ 举一反三：‎ ‎【变式1】如图,甲船以每小时海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船的北偏西的方向处,此时两船相距20海里.当甲船航行20分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里,问乙船每小时航行多少海里?‎ ‎【解析】如图，连结，‎ ‎∵，，‎ ‎∴是等边三角形，，‎ 在中，由余弦定理得:‎ ‎，‎ ‎∴‎ 因此乙船的速度的大小为 答：乙船每小时航行海里.‎ ‎【变式2】如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（ ）‎ A．a km B．km C． km D．2a km ‎【答案】B ‎ ‎【解析】利用余弦定理解△ABC. 易知∠ACB=120°，在△ABC中，由余弦定理得 ‎，‎ ‎∴km.‎