陕西省渭南市韩城市司马迁中学2020届高三第十二周实践演练数学（文）试卷

陕西省渭南市韩城市司马迁中学2020届高三第十二周实践演练数学（文）试卷

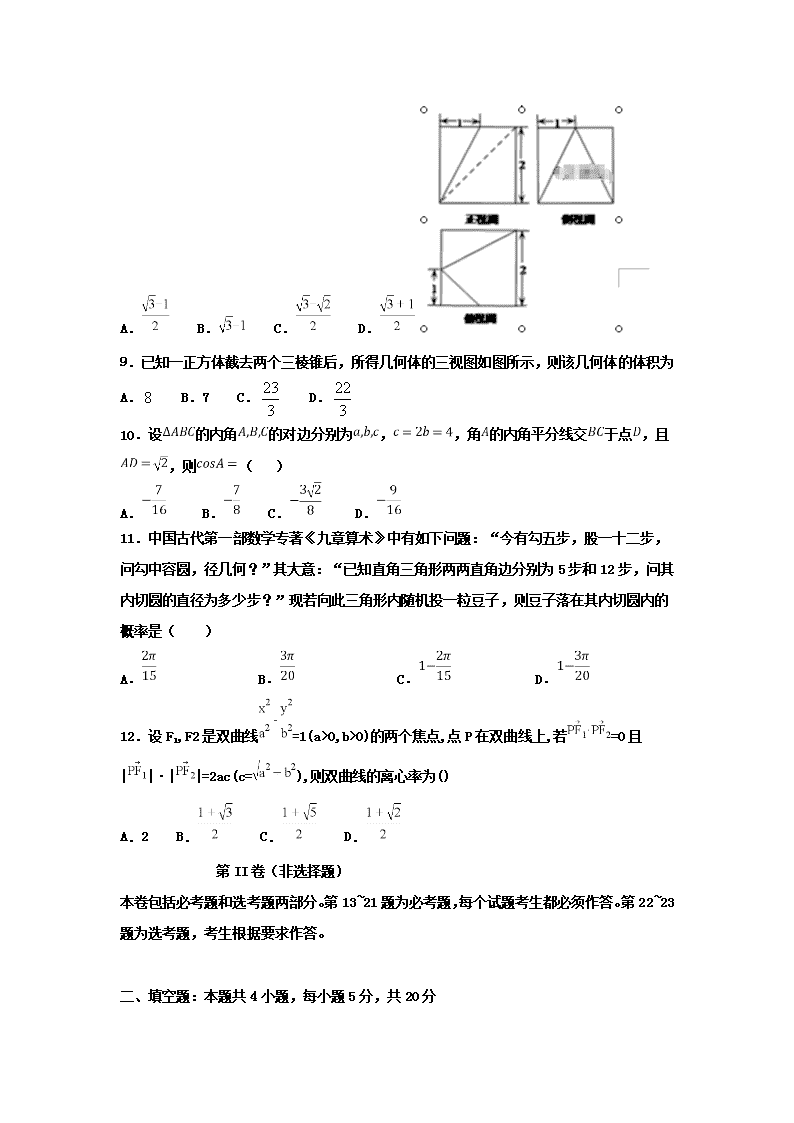
数学试卷（文）‎ 第I卷（选择题)‎ 一、单选题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知集合A＝{x|x2－x－2≤0，x∈R}，B＝{x|lg(x+1)＜1，x∈Z}，则A∩B＝（ ）‎ A．（0，2） B．[0，2] C．{0，2} D．{0，1，2}‎ ‎2．在复平面内，复数所对应的点A的坐标为（3，4），则=（ ）‎ A． B． C． D．‎ ‎3．已知函数那么在下列区间中含有函数零点的是 A． B． C． D．‎ ‎4．在区间上随机取一个数x,则事件“0≤sin x≤1”发生的概率为()‎ A． B． C． D．‎ ‎5．是直线和直线平行且不重合的 A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分也非必要条件 ‎6．若直线是圆的一条对称轴，则的值为( )‎ A．1 B． C．2 D．‎ ‎7．数列满足：，则数列前项的和为 A． B． C． D．‎ ‎8．在等腰直角中，在边上且满足：，若，则的值为（ ）‎ A． B． C． D．‎ ‎9．已知一正方体截去两个三棱锥后，所得几何体的三视图如图所示，则该几何体的体积为 A． B．7 C． D．‎ ‎10．设的内角的对边分别为，，角的内角平分线交于点，且，则（ ）‎ A． B． C． D．‎ ‎11．中国古代第一部数学专著《九章算术》中有如下问题：“今有勾五步，股一十二步，问勾中容圆，径几何？”其大意：“已知直角三角形两两直角边分别为5步和12步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆内的概率是（ ）‎ A． B． C． D．‎ ‎12．设F1,F2是双曲线=1(a>0,b>0)的两个焦点,点P在双曲线上,若=0且||·||=2ac(c=),则双曲线的离心率为()‎ A．2 B． C． D．‎ 第II卷（非选择题) ‎ 本卷包括必考题和选考题两部分。第13~21题为必考题，每个试题考生都必须作答。第22~23题为选考题，考生根据要求作答。‎ 二、填空题：本题共4小题，每小题5分，共20分 ‎13．抛物线的焦点坐标为__________．‎ ‎14．已知函数的图像为曲线，若曲线存在与直线垂直的切线，则实数的取值范围为 ．‎ ‎15．在一次连环交通事故中，只有一个人需要负主要责任，但在警察询问时，甲说：“主要责任在乙”；乙说：“丙应负主要责任”；丙说“甲说的对”；丁说：“反正我没有责任”．四人中只有一个人说的是真话，则该事故中需要负主要责任的人是_____．‎ ‎16．已知四棱椎中，底面是边长为2的菱形，且，则四棱锥体积的最大值为_____． ‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤。‎ ‎17（本小题满分12分）．已知a，b，c分别为△ABC三个内角A，B，C的对边，且acos C＋asin C－b－c＝0.‎ ‎(1)求A；‎ ‎(2)若AD为BC边上的中线，cos B＝，AD＝，求△ABC的面积．‎ ‎18（本小题满分12分）．某公司培训员工某项技能，培训有如下两种方式：‎ 方式一：周一到周五每天培训1小时，周日测试 方式二：周六一天培训4小时，周日测试 公司有多个班组，每个班组60人，现任选两组记为甲组、乙组先培训；甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如表：‎ 第一周 第二周 第三周 第四周 甲组 ‎20‎ ‎25‎ ‎10‎ ‎5‎ 乙组 ‎8‎ ‎16‎ ‎20‎ ‎16‎ 用方式一与方式二进行培训，分别估计员工受训的平均时间精确到，并据此判断哪种培训方式效率更高？‎ 在甲乙两组中，从第三周培训后达标的员工中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求这2人中至少有1人来自甲组的概率．‎ ‎19（本小题满分12分）．如图,三棱柱中,侧面 侧面,,,,为棱的中点,为的中点.‎ ‎(1) 求证:平面；‎ ‎ (2) 若,求三棱柱的体积.‎ ‎20（本小题满分12分）．椭圆，是椭圆与轴的两个交点，为椭圆C的上顶点，设直线的斜率为，直线的斜率为，．‎ ‎（1）求椭圆的离心率； ‎ ‎（2）设直线与轴交于点，交椭圆于、两点，且满足，当的面积最大时，求椭圆的方程．‎ ‎21（本小题满分12分）．已知函数，，其中．‎ ‎（1）设两曲线，有公共点，且在该点处的切线相同，用表示，并求 的最大值；‎ ‎（2）设，证明：若≥1，则对任意， ，，有 请考生在22、23题中任选一题作答，如果多做，则按所作的第一题计分。‎ ‎22(本小题满分10分)．[选修4-4：坐标系与参数方程] ‎ ‎．在直角坐标系xOy中，曲线C的参数方程为，在以O为极点，x轴的非负半轴为极轴的极坐标系中，直线l的极坐标方程为．‎ ‎（1）设曲线C与直线l的交点为A、B，求弦AB的中点P的直角坐标；‎ ‎（2）动点Q在曲线C上，在（1）的条件下，试求△OPQ面积的最大值．‎ ‎23(本小题满分10分)．[选修4-5：不等式选讲]‎ 已知 ‎（1）当时，求不等式的解集；‎ ‎（2）若不等式的解集为实数集，求实数的取值范围.‎ ‎12周文数实战演练参考答案 一．选择题 1．D2．C3．B4．C5．C6．B7．A8．A9．B10．A11．A.12．C 二．填空题 13．14．15．甲16．‎ 三．解答题 ‎17．(1)acos C＋asin C－b－c＝0，由正弦定理得sin Acos C＋sin Asin C＝sin B＋sin C，‎ 即sin Acos C＋sin Asin C＝sin(A＋C)＋sin C，‎ 又sin C≠0，所以化简得sin A－cos A＝1，所以sin(A－30°)＝.‎ 在△ABC中，0°＜A＜180°，所以A－30°＝30°，得A＝60°.‎ ‎(2)在△ABC中，因为cos B＝，所以sin B＝.‎ 所以sin C＝sin(A＋B)＝×＋×＝.‎ 由正弦定理得，.‎ 设a＝7x，c＝5x(x＞0)，则在△ABD中，AD2＝AB2＋BD2－2AB·BDcos B，‎ 即＝25x2＋×49x2－2×5x××7x×，解得x＝1，所以a＝7，c＝5，‎ 故S△ABC＝acsin B＝10.‎ ‎18．解:（1）设甲乙两组员工受训的平均时间分别为、，则 ‎（小时）‎ ‎（小时）‎ 据此可估计用方式一与方式二培训，员工受训的平均时间分别为10小时和10.9小时，因，据此可判断培训方式一比方式二效率更高；‎ ‎（2）从第三周培训后达标的员工中采用分层抽样的方法抽取6人,‎ 则这6人中来自甲组的人数为：，‎ 来自乙组的人数为：，‎ 记来自甲组的2人为：；来自乙组的4人为：，则从这6人中随机抽取 ‎2人的不同方法数有：，，，，共15种，‎ 其中至少有1人来自甲组的有：，‎ 共9种，故所求的概率..‎ ‎19． 详解：(1)连结,因为为正三角形,为棱的中点,‎ ‎ 所以,从而,又面 面,‎ 面 面 ,面,‎ 所以面,又面,所以 …①,‎ 设,由,所以,,‎ ‎,又,所以,‎ 所以,又,‎ 所以,‎ 设,则…②, ‎ 由①②及,可得平面. ‎ ‎(2)方法一:取中点,连结,则,所以面. ‎ 所以, ‎ 所以三棱柱的体积为. ‎ 方法二:取中点,连结,因为为正三角形,所以,‎ 因为面面,面 面 ,面,‎ ‎,所以面,又面,所以,‎ 又,所以平面,所以为三棱柱的高, ‎ 经计算,, ‎ 所以三棱柱的体积.‎ ‎．‎ ‎20．详解：（1），， ，， ‎ ‎， ． ‎ ‎（2）由（1）知，得，‎ 可设椭圆的方程为： ‎ 设直线的方程为：，直线与椭圆交于 两点 得 ‎ 因为直线与椭圆相交，所以，‎ 由韦达定理：，． ‎ 又，所以，代入上述两式有：， ‎ 所以 ‎ ‎， ‎ 当且仅当时，等号成立， 此时， ‎ 代入，有成立，所以所求椭圆的方程为：．‎ ‎21． 详解：（1）设的图象交于点，则有，‎ 即 ①‎ 又由题意知，即 ②‎ 由②解得 ‎ 将代入（1）整理得 令，则 当时，单调递增，当时单调递减，‎ 所以，即，的最大值为 ‎ ‎（2）证明：不妨设，‎ 变形得 令，，‎ ‎，‎ 所以 在上单调递增，，‎ 即成立 同理可证,当时,命题也成立 ‎ 综上, 对任意，，，不等式成立.‎ ‎22． 【详解】‎ 由消去参数，得，‎ 由得，得，‎ 联立消去并整理得，‎ 设，，，，‎ 则，，‎ ‎，．‎ ‎（2）|OP|==，‎ 所以直线OP的方程为x+4y=0，‎ 设Q（2cosα，sinα），‎ 则点Q到直线x+4y=0的距离d=≤=，‎ ‎=|OP|d≤××=．‎ ‎.‎ ‎23． （1）当时，，‎ 当时，由得，得，或，‎ 所以.‎ 当时 ,由 得 ,‎ 解得，或. ‎ 所以 ‎ 当时，由得，‎ 解得，或.‎ 所以 ‎ 综上 当时，的解集为.‎ ‎（2）的解集为实数集，‎ 当时， ，‎ 当时， ，‎ 的最大值为.‎ 实数的取值范围为.‎