- 2021-07-01 发布 |
- 37.5 KB |
- 28页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
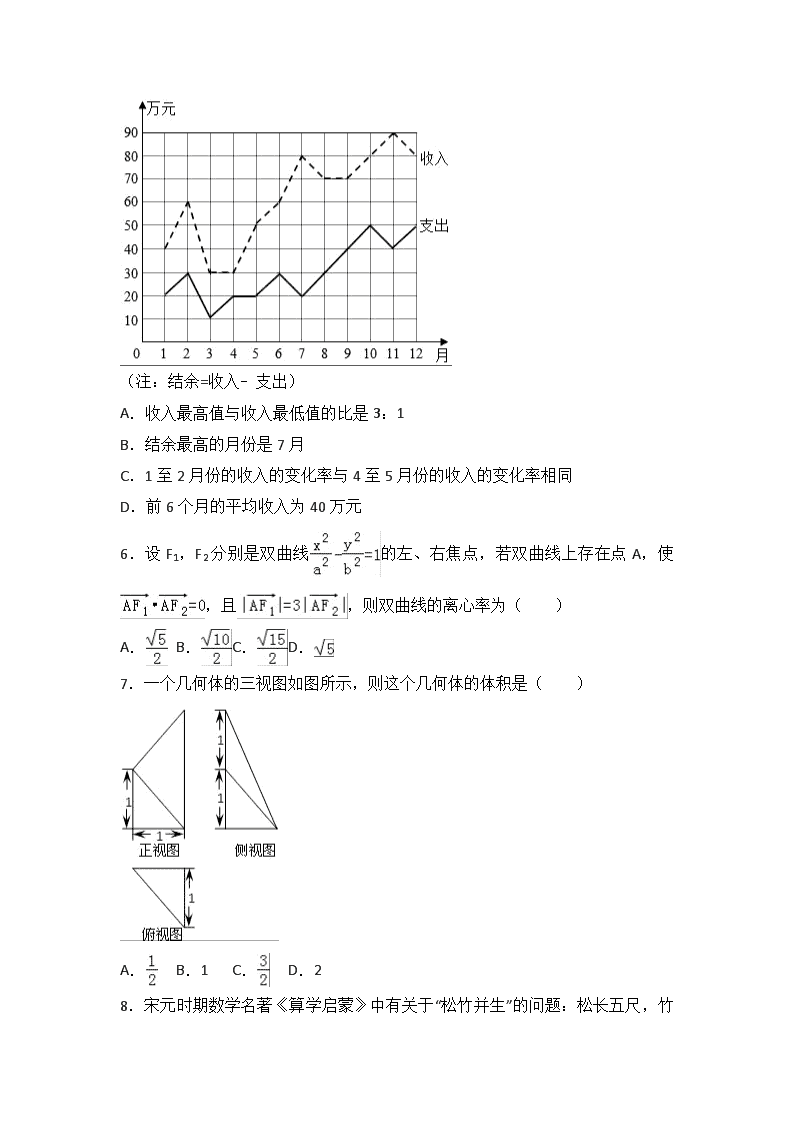
数学卷·2018届湖北省襄阳五中高二下学期3月月考数学试卷(文科) (解析版)
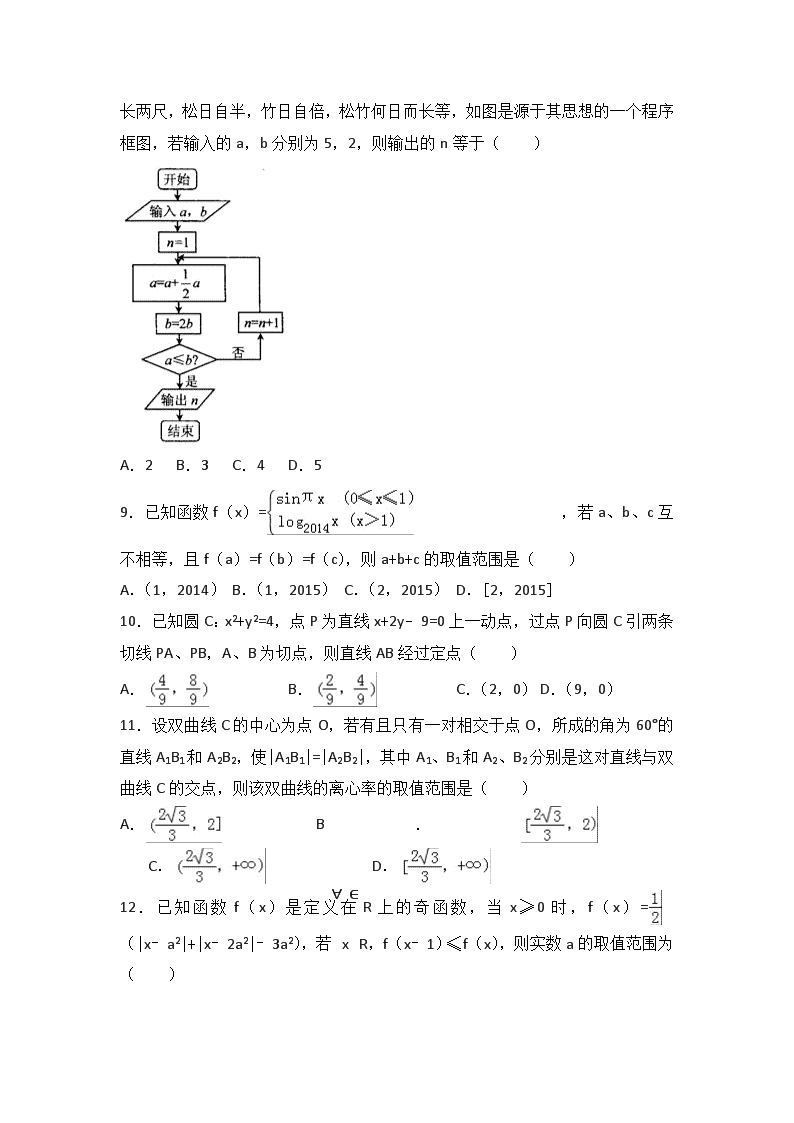
2016-2017学年湖北省襄阳五中高二(下)3月月考数学试卷(文科) 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确的答案填涂在答题卡上. 1.已知复数z=1﹣i(i是虚数单位),则﹣z2的共轭复数是( ) A.1﹣3i B.1+3i C.﹣1+3i D.﹣1﹣3i 2.设集合A={x|x<2},B={y|y=2x﹣1,x∈A},则A∩B=( ) A.(﹣∞,3) B.[2,3) C.(﹣∞,2) D.(﹣1,2) 3.下列选项叙述错误的是( ) A.命题“若x≠l,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1” B.若p∨q为真命题,则p,q均为真命题 C.若命题p:∀x∈R,x2+x+1≠0,则¬p:∃x∈R,x2+x+1=0 D.“x>2”是“x2﹣3x+2>0”的充分不必要条件 4.有一长、宽分别为50m、30m的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是( ) A. B. C. D. 5.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( ) (注:结余=收入﹣支出) A.收入最高值与收入最低值的比是3:1 B.结余最高的月份是7月 C.1至2月份的收入的变化率与4至5月份的收入的变化率相同 D.前6个月的平均收入为40万元 6.设F1,F2分别是双曲线的左、右焦点,若双曲线上存在点A,使,且,则双曲线的离心率为( ) A. B. C. D. 7.一个几何体的三视图如图所示,则这个几何体的体积是( ) A. B.1 C. D.2 8.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n等于( ) A.2 B.3 C.4 D.5 9.已知函数f(x)=,若a、b、c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( ) A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015] 10.已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( ) A. B. C.(2,0) D.(9,0) 11.设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1、B1和A2、B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( ) A. B. C. D. 12.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若∀x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( ) A.[﹣,] B.[﹣,] C.[﹣,] D.[﹣,] 二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上,答错位置,书写不清,模棱两可均不得分. 13.直角坐标平面上一机器人在行进中始终保持到两点A(a,0)和B(0,1)的距离相等,且机器人也始终接触不到直线L:y=x+1,则a的值为 . 14.甲、乙、丙、丁四支足球队举行“贺岁杯”足球友谊赛,每支球队都要与其它三支球队进行比赛,且比赛要分出胜负.若甲、乙、丙队的比赛成绩分别是两胜一负、全败、一胜两负,则丁队的比赛成绩是 . 15.某校今年计划招聘女教师x人,男教师y人,若x、y满足,则该学校今年计划招聘教师最多 人. 16.在△ABC中,BC=8,sinB﹣sinC=sinA,D点是边BC的中点,则∠ADC的取值范围为 . 三、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求数列{an}的通项公式; (Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn. 18.某校高三文科500名学生参加了1月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机表法从中抽取100名学生进行统计分析,抽出的100名学生的数学、语文成绩如表: 语文 优 良 及格 数学 优 8 m 9 良 9 n 11 及格 8 9 11 (1)将学生编号为000,001,002,…499,500,若从第五行第五列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机数表的第4~第7行); 12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76 55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 (2)若数学成绩优秀率为35%,求m,n的值; (3)在语文成绩为良的学生中,已知m≥13,n≥11,求数学成绩“优”比良的人数少的概率. 19.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°. (1)求证:CE∥平面PAB; (2)若PA=2AB=2,求四面体P﹣ACE的体积. 20.已知点F(﹣2,0)在以原点为圆心的圆O内,且过F的最短的弦长为2. (1)求圆O的方程; (2)过F任作一条与两坐标标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,求M点的坐标. 21.如图,曲线Г由曲线C1: +=1(a>b>0,y≤0)和曲线C2:﹣=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点, (1)若F2(2,0),F3(﹣6,0),求曲线Г的方程; (2)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上; (3)对于(Ⅰ)中的曲线Г,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值. 22.已知f(x)= (1)求函数f(x)的最小正周期及单调递增区间. (2)当时,方程f(x)﹣m=0有实数解,求实数m的取值范围. 2016-2017学年湖北省襄阳五中高二(下)3月月考数学试卷(文科) 参考答案与试题解析 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确的答案填涂在答题卡上. 1.已知复数z=1﹣i(i是虚数单位),则﹣z2的共轭复数是( ) A.1﹣3i B.1+3i C.﹣1+3i D.﹣1﹣3i 【考点】复数代数形式的乘除运算. 【分析】把复数z=1﹣i,代入﹣z2,然后利用复数代数形式的乘除运算化简,则﹣z2的共轭复数可求. 【解答】解:由复数z=1﹣i, 得﹣z2==, 则﹣z2的共轭复数是:1﹣3i. 故选:A. 2.设集合A={x|x<2},B={y|y=2x﹣1,x∈A},则A∩B=( ) A.(﹣∞,3) B.[2,3) C.(﹣∞,2) D.(﹣1,2) 【考点】交集及其运算. 【分析】由指数函数的值域和单调性,化简集合B,再由交集的定义,即可得到所求. 【解答】解:集合A={x|x<2}=(﹣∞,2),B={y|y=2x﹣1,x∈A}, 由x<2,可得y=2x﹣1∈(﹣1,3), 即B={y|﹣1<y<3}=(﹣1,3), 则A∩B=(﹣1,2). 故选:D. 3.下列选项叙述错误的是( ) A.命题“若x≠l,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1” B.若p∨q为真命题,则p,q均为真命题 C.若命题p:∀x∈R,x2+x+1≠0,则¬p:∃x∈R,x2+x+1=0 D.“x>2”是“x2﹣3x+2>0”的充分不必要条件 【考点】命题的真假判断与应用. 【分析】A“若p则q,“的逆否命题为“若﹣p则﹣q“.故A正确;B p∨q为真命题说明p和q中至少有一个为真;C是全称命题与存在性命题的转化;D从充要条件方面判断. 【解答】解:A原命题为“若p则q,“,则它的逆否命题为“若﹣p则﹣q“.故正确; B当p,q中至少有一个为真命题时,则p∨q为真命题.故错误. C正确. D 由x2一3x+2>0解得x<1或x>2 显然x>2⇒x<1或x>2 但x<1或x>2不能得到x>2 故“x>2”是“x2一3x+2>0”的充分不必要条件,故正确. 故选B 4.有一长、宽分别为50m、30m的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是( ) A. B. C. D. 【考点】几何概型. 【分析】由题意可知所有可能结果用周长160表示,事件发生的结果可用两条线段的长度和60表示,即可求得. 【解答】解:当该人在池中心位置时,呼唤工作人员的声音可以传,那么当构成如图所示的三角形时,工作人员才能及时的听到呼唤声, 所有可能结果用周长160表示,事件发生的结果可用两条线段的长度和60表示,. 故选B. 5.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( ) (注:结余=收入﹣支出) A.收入最高值与收入最低值的比是3:1 B.结余最高的月份是7月 C.1至2月份的收入的变化率与4至5月份的收入的变化率相同 D.前6个月的平均收入为40万元 【考点】函数的图象与图象变化. 【分析】根据折现统计图即可判断各选项. 【解答】解:由图可知,收入最高值为90万元,收入最低值为30万元,其比是3:1,故A正确, 由图可知,结余最高为7月份,为80﹣20=60,故B正确, 由图可知,1至2月份的收入的变化率为与4至5月份的收入的变化率相同,故C正确, 由图可知,前6个月的平均收入为(40+60+30+30+50+60)=45万元,故D错误, 故选:D. 6.设F1,F2分别是双曲线的左、右焦点,若双曲线上存在点A,使,且,则双曲线的离心率为( ) A. B. C. D. 【考点】双曲线的简单性质. 【分析】由题意,可由条件,且及双曲线的定义建立方程用a表示出c,从而求得离心率选出正确选项 【解答】解:由题意得, 由,及得 所以=a,即c=a ∴e= 故选B 7.一个几何体的三视图如图所示,则这个几何体的体积是( ) A. B.1 C. D.2 【考点】由三视图求面积、体积. 【分析】由已知中三视图,我们可以判断出几何体的形状及几何特征,求出其底面面积、高等关键几何量后,代入棱锥体积公式,即可得到答案. 【解答】解:由已知易得该几何体是一个以正视图为底面,以1为高的四棱锥 由于正视图是一个上底为1,下底为2,高为1的直角梯形 故棱锥的底面面积S== 则V=== 故选A 8.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n等于( ) A.2 B.3 C.4 D.5 【考点】程序框图. 【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【解答】解:当n=1时,a=,b=4,满足进行循环的条件, 当n=2时,a=,b=8满足进行循环的条件, 当n=3时,a=,b=16满足进行循环的条件, 当n=4时,a=,b=32不满足进行循环的条件, 故输出的n值为4, 故选C. 9.已知函数f(x)=,若a、b、c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( ) A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015] 【考点】分段函数的应用. 【分析】根据题意,在坐标系里作出函数f(x)的图象,根据f(a)=f(b)=f(c),确定a,b,c的大小,即可得出a+b+c的取值范围. 【解答】解:作出函数的图象如图, 直线y=m交函数图象于如图, 不妨设a<b<c, 由正弦曲线的对称性,可得(a,m)与(b,m)关于直线x=对称, 因此a+b=1, 当直线y=m=1时,由log2014x=1, 解得x=2014,即x=2014, ∴若满足f(a)=f(b)=f(c),(a、b、c互不相等), 由a<b<c可得1<c<2014, 因此可得2<a+b+c<2015, 即a+b+c∈(2,2015). 故选:C. 10.已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( ) A. B. C.(2,0) D.(9,0) 【考点】直线与圆的位置关系. 【分析】根据题意设P的坐标为P(9﹣2m,m),由切线的性质得点A、B在以OP为直径的圆C上,求出圆C的方程,将两个圆的方程相减求出公共弦AB所在的直线方程,再求出直线AB过的定点坐标. 【解答】解:因为P是直线x+2y﹣9=0的任一点,所以设P(9﹣2m,m), 因为圆x2+y2=4的两条切线PA、PB,切点分别为A、B, 所以OA⊥PA,OB⊥PB, 则点A、B在以OP为直径的圆上,即AB是圆O和圆C的公共弦, 则圆心C的坐标是(,),且半径的平方是r2=, 所以圆C的方程是(x﹣)2+(y﹣)2=,① 又x2+y2=4,②, ②﹣①得,(2m﹣9)x﹣my+4=0,即公共弦AB所在的直线方程是:(2m﹣9)x﹣my+4=0, 即m(2x﹣y)+(﹣9x+4)=0, 由得x=,y=, 所以直线AB恒过定点(,), 故选A. 11.设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1、B1和A2、B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( ) A. B. C. D. 【考点】双曲线的简单性质. 【分析】不妨令双曲线的方程为,由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,由满足条件的直线只有一对,得,由此能求出双曲线的离心率的范围. 【解答】解:不妨令双曲线的方程为, 由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,如图, 又∵满足条件的直线只有一对, 当直线与x轴夹角为30°时,双曲线的渐近线与x轴夹角大于30°, 双曲线与直线才能有交点A1,A2,B1,B2, 若双曲线的渐近线与x轴夹角等于30°,则无交点, 则不可能存在|A1B1|=|A2B2|, 当直线与x轴夹角为60°时,双曲线渐近线与x轴夹角大于60°, 双曲线与直线有一对交点A1,A2,B1,B2, 若双曲线的渐近线与x轴夹角等于60°,也满足题中有一对直线, 但是如果大于60°,则有两对直线.不符合题意, ∴tan30°,即, ∴, ∵b2=c2﹣a2,∴,∴, ∴, ∴双曲线的离心率的范围是. 故选:A. 12.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若∀x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( ) A.[﹣,] B.[﹣,] C.[﹣,] D.[﹣,] 【考点】函数恒成立问题;函数奇偶性的判断;函数最值的应用. 【分析】把x≥0时的f(x)改写成分段函数,求出其最小值,由函数的奇偶性可得x<0时的函数的最大值,由对∀x∈R,都有f(x﹣1)≤f(x),可得2a2﹣(﹣4a2)≤1,求解该不等式得答案. 【解答】解:当x≥0时, f(x)=, 由f(x)=x﹣3a2,x>2a2,得f(x)>﹣a2; 当a2<x≤2a2时,f(x)=﹣a2; 由f(x)=﹣x,0≤x≤a2,得f(x)≥﹣a2. ∴当x>0时,. ∵函数f(x)为奇函数, ∴当x<0时,. ∵对∀x∈R,都有f(x﹣1)≤f(x), ∴2a2﹣(﹣4a2)≤1,解得:. 故实数a的取值范围是. 故选:B. 二、填空题:本题共4小题,每小题5分,共20分.请将答案填在答题卡对应题号的位置上,答错位置,书写不清,模棱两可均不得分. 13.直角坐标平面上一机器人在行进中始终保持到两点A(a,0)和B(0,1)的距离相等,且机器人也始终接触不到直线L:y=x+1,则a的值为 1 . 【考点】点到直线的距离公式. 【分析】由题意可得:线段AB的垂直平分线与直线L平行,即可得出. 【解答】解:由题意可得:线段AB的垂直平分线与直线L平行: 则×1=﹣1,解得a=1. 故答案为:1. 14.甲、乙、丙、丁四支足球队举行“贺岁杯”足球友谊赛,每支球队都要与其它三支球队进行比赛,且比赛要分出胜负.若甲、乙、丙队的比赛成绩分别是两胜一负、全败、一胜两负,则丁队的比赛成绩是 全胜 . 【考点】进行简单的合情推理. 【分析】 根据题意可得,共有6胜6负,由甲,乙,丙的成绩,运用补集思想即可求出丁的成绩. 【解答】解:由题意可得,甲、乙、丙、丁四支足球队举行“贺岁杯”足球友谊赛,每支球队都要与其它三支球队进行比赛,且比赛要分出胜负,则共需进行=6场, ∵每场都会产生胜方和负方, ∴比赛共产生6胜6负, ∵甲、乙、丙队的比赛成绩分别是两胜一负、全败、一胜两负,已有3胜6负, ∴丁队的比赛成绩是全胜,即3胜. 故答案为:全胜. 15.某校今年计划招聘女教师x人,男教师y人,若x、y满足,则该学校今年计划招聘教师最多 10 人. 【考点】简单线性规划. 【分析】作出不等式组对应的平面区域,则目标函数为z=x+y,利用线性规划的知识进行求解即可. 【解答】解:设z=x+y, 作出不等式组对应的平面区域如图: 由z=x+y得y=﹣x+z, 平移直线y=﹣x+z, 由图象可知当直线y=﹣x+z经过点A时, 直线y=﹣x+z的截距最大, 此时z最大.但此时z最大值取不到, 由图象当直线经过整点E(5,5)时,z=x+y取得最大值, 代入目标函数z=x+y得z=5+5=10. 即目标函数z=x+y的最大值为10. 故答案为:10. 16.在△ABC中,BC=8,sinB﹣sinC=sinA,D点是边BC的中点,则∠ADC的取值范围为 . 【考点】正弦定理. 【分析】以BC所在的直线为x轴,以线段BC的垂直平分线为y轴,建立平面直角坐标系,由已知得A点的轨迹为以BC焦点的双曲线的一支且除去顶点,由此能求出A的轨迹方程.再利用直线与双曲线相切即可得出. 【解答】解:以BC所在的直线为x轴,以线段BC的垂直平分线为y轴, 建立平面直角坐标系, 则B(﹣4,0),C(4,0), △ABC中, ==, ∵sinC﹣sinB=sinA, ∴|AB|﹣|AC|=|BC|=4<|BC|=8, ∴A点的轨迹为以BC焦点的双曲线的一支且除去顶点. ∴其方程为: =1.(x>2). 设直线y=kx与上述曲线相切,则(3﹣k2)x2﹣12=0, 利用△=0﹣4×(﹣12)×(3﹣k2)=0,解得k=. ∴∠ADC∈. 故答案为:. 三、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求数列{an}的通项公式; (Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn. 【考点】数列的求和;等差数列的通项公式. 【分析】(Ⅰ)依题意 a3+a8﹣(a2+a7)=2d=﹣6,从而d=﹣3.由此能求出数列{an}的通项公式. (Ⅱ)由数列{an+bn}是首项为1,公比为c的等比数列,得,所以.所以 =.由此能求出{bn}的前n项和Sn. 【解答】(Ⅰ)解:设等差数列{an}的公差是d. 依题意 a3+a8﹣(a2+a7)=2d=﹣6,从而d=﹣3. 所以 a2+a7=2a1+7d=﹣23,解得 a1=﹣1. 所以数列{an}的通项公式为 an=﹣3n+2. (Ⅱ)解:由数列{an+bn}是首项为1,公比为c的等比数列, 得,即, 所以. 所以 =. 从而当c=1时,; 当c≠1时,. 18.某校高三文科500名学生参加了1月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机表法从中抽取100名学生进行统计分析,抽出的100名学生的数学、语文成绩如表: 语文 优 良 及格 数学 优 8 m 9 良 9 n 11 及格 8 9 11 (1)将学生编号为000,001,002,…499,500,若从第五行第五列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机数表的第4~第7行); 12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76 55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 (2)若数学成绩优秀率为35%,求m,n的值; (3)在语文成绩为良的学生中,已知m≥13,n≥11,求数学成绩“优”比良的人数少的概率. 【考点】列举法计算基本事件数及事件发生的概率. 【分析】(1)利用随机数表法能求出5个人的编号. (2)由=0.35,能求出m,n. (3)由题意 m+n=35,且m≥13,n≥11,利用列举法能求出数学成绩“优”比良的人数少的概率. 【解答】解:(1)由随机数表法得到5个人的编号依次为:385,482,462,231,309.… (2)由=0.35,得m=18, 因为8+9+8+18+n+9+9+11+11=100,得n=17.… (3)由题意 m+n=35,且m≥13,n≥11, 所以满足条件的(m,n)有: (13,22)、(14,21)、(15,20)、(16,19)、(17,18)、(18,17)、 (19,16)、(20,15)、(21,14)、(22,13)、(23,12)、(24,11)共12种, 且每组出现都是等可能的.… 记:“数学成绩“优”比“良”的人数少”为事件M, 则事件M包含的基本事件有(13,22)、(14,21)、(15,20)、(16,19)、(17,18)共5种, 所以P(M)=.… 19.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°. (1)求证:CE∥平面PAB; (2)若PA=2AB=2,求四面体P﹣ACE的体积. 【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定. 【分析】(1)证明F为AD的中点,利用三角形中位线,得出EF∥PA,从而EF∥平面PAB.证出CF∥AB,从而CF∥平面PAB.最后结合面面平行的判定定理,得到平面CEF∥平面PAB,所以CE∥平面PAB; (2)利用等体积法,根据锥体体积公式算出三棱锥P﹣ACE的体积. 【解答】(1)证明:∵ABC=∠ACD=90°,∠BAC=∠CAD=60°, ∴∠FDC=30°, ∵∠FCD=30°, ∴∠ACF=60°, ∴AF=CF=DF, ∴F为AD的中点, ∵E为PD的中点, ∴△PAD中,EF是中位线,可得EF∥PA ∵EF⊄平面PAB,PA⊂平面PAB,∴EF∥平面PAB; ∵∠BAC=∠ACF=60°, ∴CF∥AB ∵CF⊄平面PAB,AB⊂平面PAB,∴CF∥平面PAB ∵EF、CF是平面CEF内的相交直线, ∴平面CEF∥平面PAB ∵CE⊂面CEF,∴CE∥平面PAB; (2)解:∵EF∥AP, ∴EF∥平面APC, ∵∠ABC=∠ACD=90°,∠BAC=60°,PA=2AB=2, ∴AC=2AB=2,CD==2, ∴VP﹣ACE=VE﹣PAC=VF﹣PAC=VP﹣ACF=S△ACD×PA==. 20.已知点F(﹣2,0)在以原点为圆心的圆O内,且过F的最短的弦长为2. (1)求圆O的方程; (2)过F任作一条与两坐标标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,求M点的坐标. 【考点】直线与圆的位置关系. 【分析】(1)由题意知:过F且垂直与x轴的弦长最短,由此能求出圆O的方程. (2)设直线AB的方程为x=ky﹣2(k≠0),代入圆方程x2+y2=5,得(k2+1)y2﹣4ky﹣1=0,由此利用韦达定理,结合已知性质能求出M点的坐标. 【解答】解:(1)由题意知:过F且垂直与x轴的弦长最短, 设圆O的半径为r,则r=, ∴圆O的方程为x2+y2=5.… (2)弦AB过F且与两坐标轴都不垂直,可设直线AB的方程为x=ky﹣2(k≠0), 并将它代入圆方程x2+y2=5,得:(ky﹣2)2+y2=5,即(k2+1)y2﹣4ky﹣1=0, 设A(x1,y1),B(x2,y2),则,y1y2=, 设M(m,0),∵∠AMB被x轴平分,∴kAM+kBM=0, 即+=0,y1(x2﹣m)+y2(x1﹣m)=0, 即y1(ky2﹣2)+y2(ky1﹣2)﹣(y1﹣y2)m=0, ∴2ky1y2﹣(y1+y2)(m+2)=0, ∴2k×﹣×(m+2)=0, ∵k≠0,∴1+2(m﹣2)=0,解得m=﹣, ∴M点的坐标(﹣,0). 21.如图,曲线Г由曲线C1: +=1(a>b>0,y≤0)和曲线C2:﹣=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点, (1)若F2(2,0),F3(﹣6,0),求曲线Г的方程; (2)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上; (3)对于(Ⅰ)中的曲线Г,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值. 【考点】曲线与方程. 【分析】(1)由F2(2,0),F3(﹣6,0),可得,解出即可; (2)设点A(x1,y1),B(x2,y2),M(x0,y0),设直线l:y=(x﹣m),与椭圆方程联立化为2x2﹣2mx+(m2﹣a2)=0,利用△>0,根与系数的关系、中点坐标公式,证明即可. (3)由(1)知,曲线=1(y≤0)F4(6,0).设直线l1 的方程为x=ny+6(n>0).与椭圆方程联立可得(5+4n2)y2+48ny+64=0,利用根与系数的关系、弦长公式、三角形的面积计算公式、基本不等式的性质即可得出. 【解答】(1)解:∵F2(2,0),F3(﹣6,0), ∴, 解得, 则曲线Γ的方程为=1(y≤0)和=1(y>0). (2)证明:曲线C2的渐近线为y=±x, 设直线l:y=(x﹣m),代入C1: +=1,化为2x2﹣2mx+(m2﹣a2)=0, △=4m2﹣8(m2﹣a2)>0, 解得﹣a<m<a. 又由数形结合知a≤m<a. 设点A(x1,y1),B(x2,y2),M(x0,y0), 则x1+x2=m,x1x2=, ∴x0=,y0=﹣, ∴y0=﹣x0,即点M在直线y=﹣x上. (3)由(1)知,曲线C1: =1(y≤0),点F4(6,0). 设直线l1的方程为x=ny+6(n>0). 联立化为(5+4n2)y2+48ny+64=0, △=(48n)2﹣4×64×(5+4n2)>0,化为n2>1. 设C(x3,y3),D(x4,y4), ∴y3+y4=﹣,y3y4=. ∴|y3﹣y4|=, △CDF1面积S=, 令t=>0,∴n2=t2+1, ∴S=≤,当且仅当t=,即n=时等号成立,△CDF1面积的最大值为. 22.已知f(x)= (1)求函数f(x)的最小正周期及单调递增区间. (2)当时,方程f(x)﹣m=0有实数解,求实数m的取值范围. 【考点】三角函数中的恒等变换应用;正弦函数的图象. 【分析】(1)先化简求得解析式,根据正弦函数的图象和性质即可求得函数f(x)的最小正周期及单调递增区间. (2)先求得,从而可得,由f(x)=m,即可求得实数m的取值范围. 【解答】解:(1)∵ ∴… ∴最小正周期为π… 令∴.函数f(x)=sinz﹣1的单调递增区间是 , 由, 得, ∴函数f(x)的单调递增区间是… (2)当时,, , , ∵f(x)=m, ∴….查看更多