- 2021-07-01 发布 |
- 37.5 KB |
- 2页
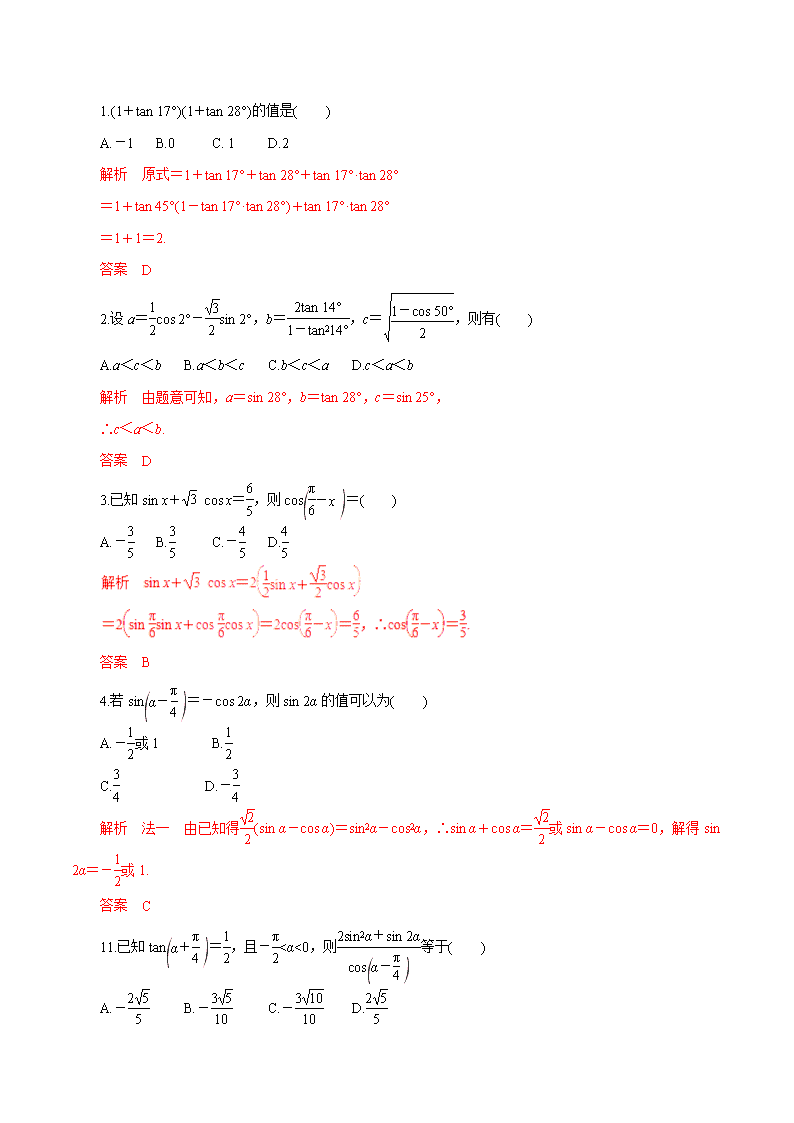
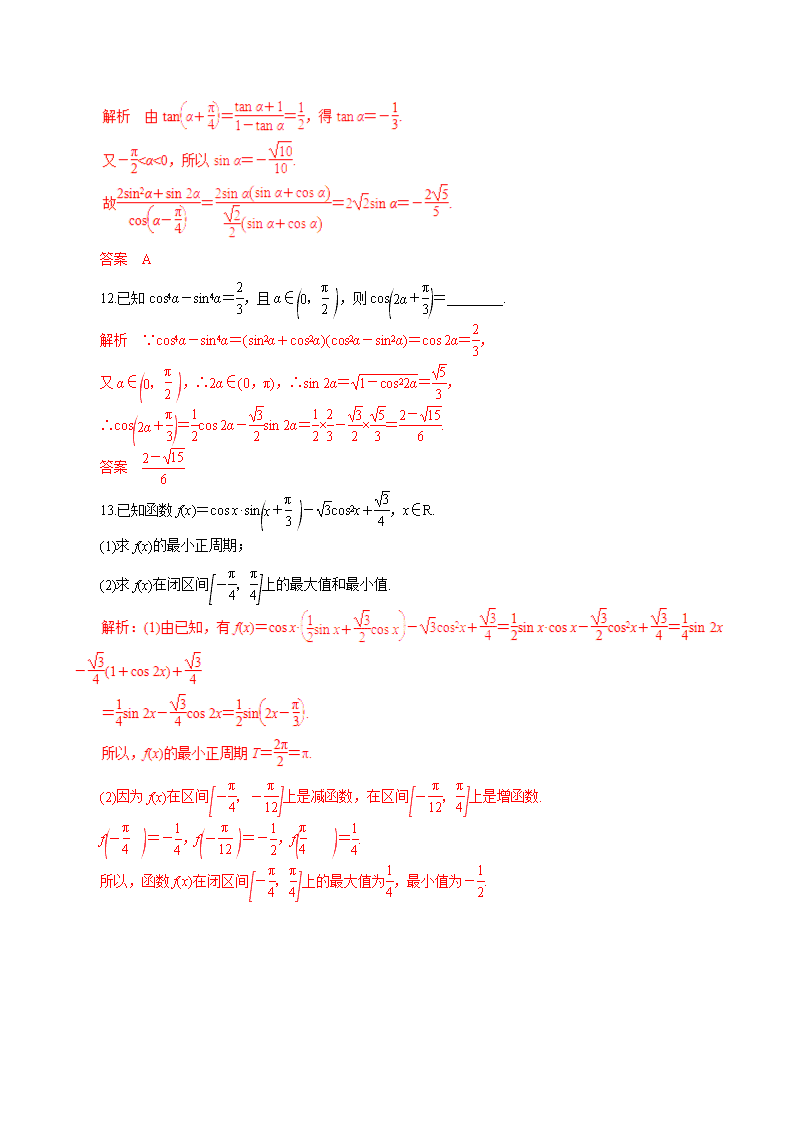
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题14+两角和与差的三角函数(题型专练)-2019年高考数学(文)热点题型和提分秘籍
1.(1+tan 17°)(1+tan 28°)的值是( ) A.-1 B.0 C. 1 D.2 解析 原式=1+tan 17°+tan 28°+tan 17°·tan 28° =1+tan 45°(1-tan 17°·tan 28°)+tan 17°·tan 28° =1+1=2. 答案 D 2.设a=cos 2°-sin 2°,b=,c=,则有( ) A.a<c<b B.a<b<c C.b<c<a D.c<a<b 解析 由题意可知,a=sin 28°,b=tan 28°,c=sin 25°, ∴c<a<b. 答案 D 3.已知sin x+ cos x=,则cos=( ) A.- B. C.- D. 答案 B 4.若sin=-cos 2α,则sin 2α的值可以为( ) A.-或1 B. C. D.- 解析 法一 由已知得(sin α-cos α)=sin2α-cos2α,∴sin α+cos α=或sin α-cos α=0,解得sin 2α=-或1. 答案 C 11.已知tan=,且-<α<0,则等于( ) A.- B.- C.- D. 答案 A 12.已知cos4α-sin4α=,且α∈,则cos=________. 解析 ∵cos4α-sin4α=(sin2α+cos2α)(cos2α-sin2α)=cos 2α=, 又α∈,∴2α∈(0,π),∴sin 2α==, ∴cos=cos 2α-sin 2α=×-×=. 答案 13.已知函数f(x)=cos x·sin-cos2x+,x∈R. (1)求f(x)的最小正周期; (2)求f(x)在闭区间上的最大值和最小值. (2)因为f(x)在区间上是减函数,在区间上是增函数. f=-,f=-,f=. 所以,函数f(x)在闭区间上的最大值为,最小值为-. 查看更多