- 2021-06-30 发布 |
- 37.5 KB |
- 3页


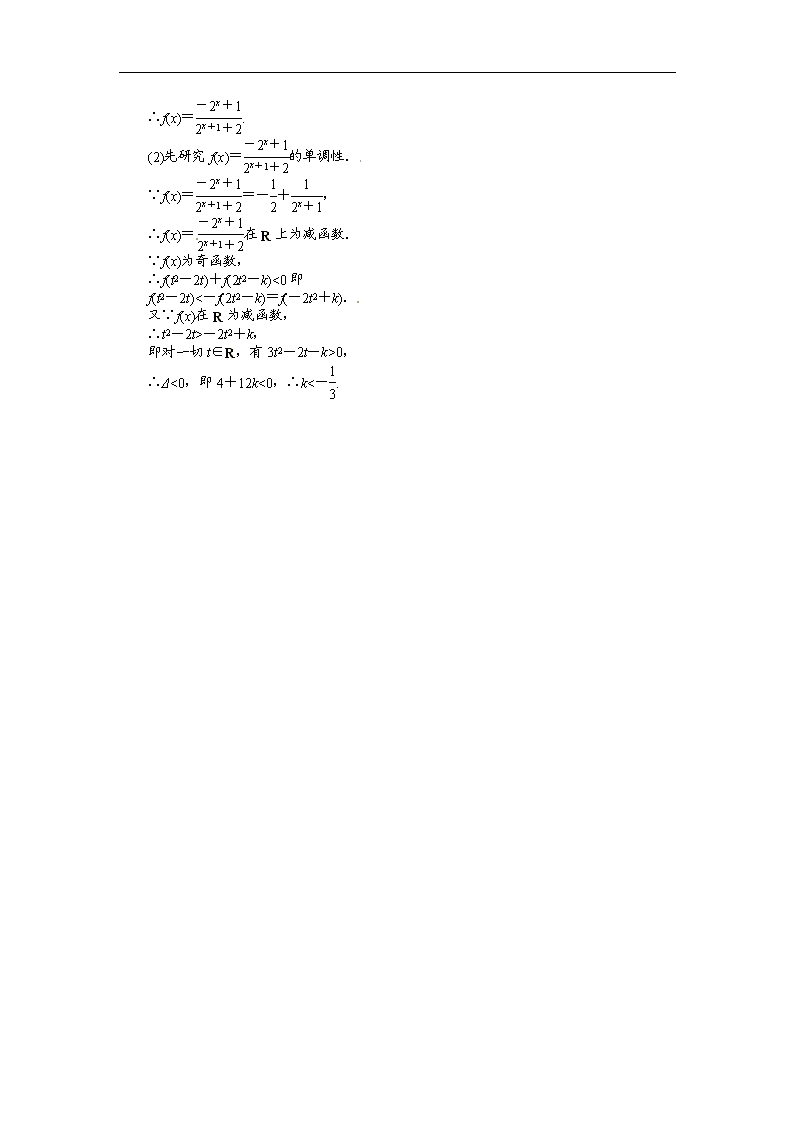
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学人教A版必修一教学训练(教师版)2_1_2_2
(本栏目内容,在学生用书中以活页形式分册装订!) 一、选择题(每小题5分,共20分) 1.函数y=a|x|(0<a<1)的图象是( ) 解析: 由y=a|x|=,且0<a<1,知C正确. 答案: C 2.下列四个函数中,值域为(0,+∞)的函数是( ) A.y=2 B.y= C.y= D.y=2-x 解析: 在A中,∵≠0,∴2≠1, 即y=2的值域为(0,1)∪(1,+∞). 在B中,2x-1≥0, ∴y=的值域为[0,+∞). 在C中,∵2x>0, ∴2x+1>1. ∴y=的值域为(1,+∞). 在D中,∵2-x∈R,∴y=2-x>0. ∴y=2-x的值域为(0,+∞).故选D. 答案: D 3.设函数f(x)=若f(x0)>1,则x0的取值范围是( ) A.(-1,1) B.(-1,+∞) C.(-∞,-2) D.(-∞,-1)∪(1,+∞) 解析: 由题意知或 解得:x0<-1或x0>1,故选D. 答案: D 4.若函数f(x)=是R上的增函数,则实数a的取值范围为( )[来源:学科网ZXXK] A.(1,+∞) B.(1,8) C.[4,8) D.(4,8) 解析: 函数f(x)= 是R上的增函数;则 ∴4≤a<8,故选C. 答案: C 二、填空题(每小题5分,共10分) 5.设函数f(x)=x(ex+ae-x),x∈R,是偶函数,则实数a=________. 解析: ∵f(x)为偶函数 ∴f(-x)=f(x),则(a+1)·e2x+(a+1)=0 ∴a=-1. 答案: -1 6.已知函数f(x)=ax(a>0且a≠1)在x∈[-2,2]上恒有f(x)<2,则实数a的取值范围为________. 解析: 当a>1时,f(x)=ax在[-2,2]上为增函数, ∴f(x)max=f(2), 又∵x∈[-2,2]时,f(x)<2恒成立, ∴,即, 解得1查看更多