- 2021-06-30 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习苏教版巧用导数解决实际应用问题学案
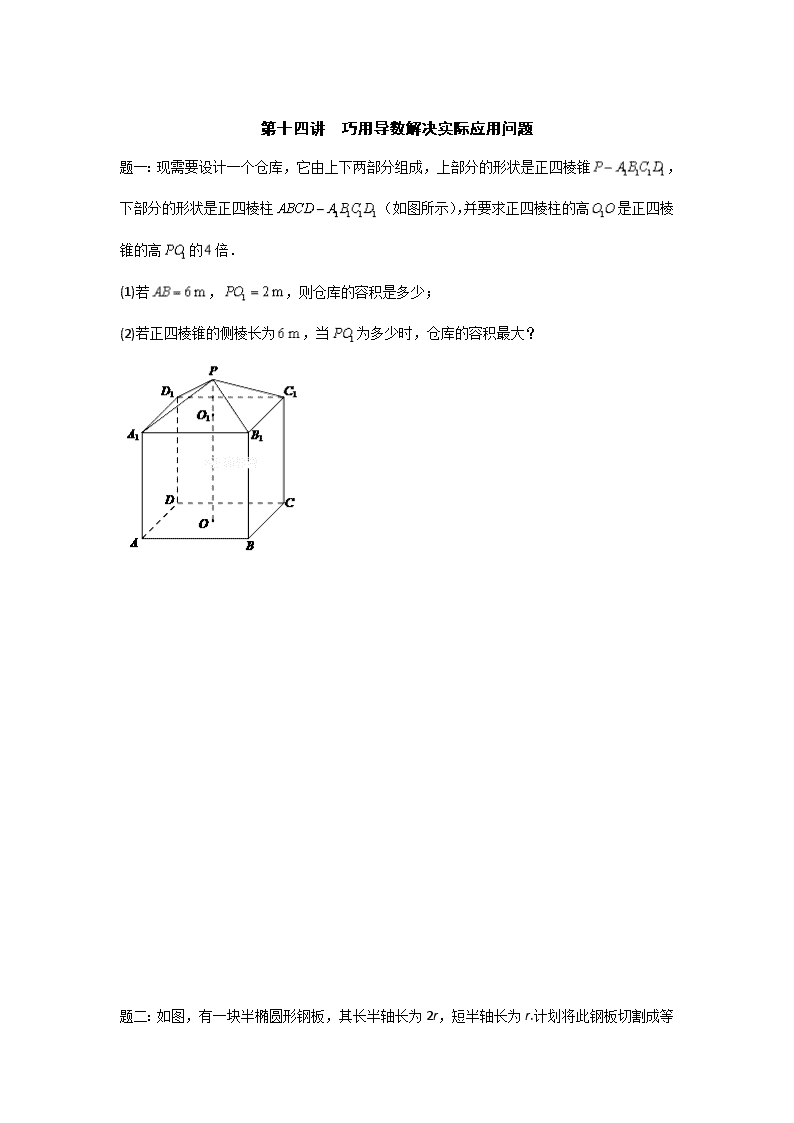
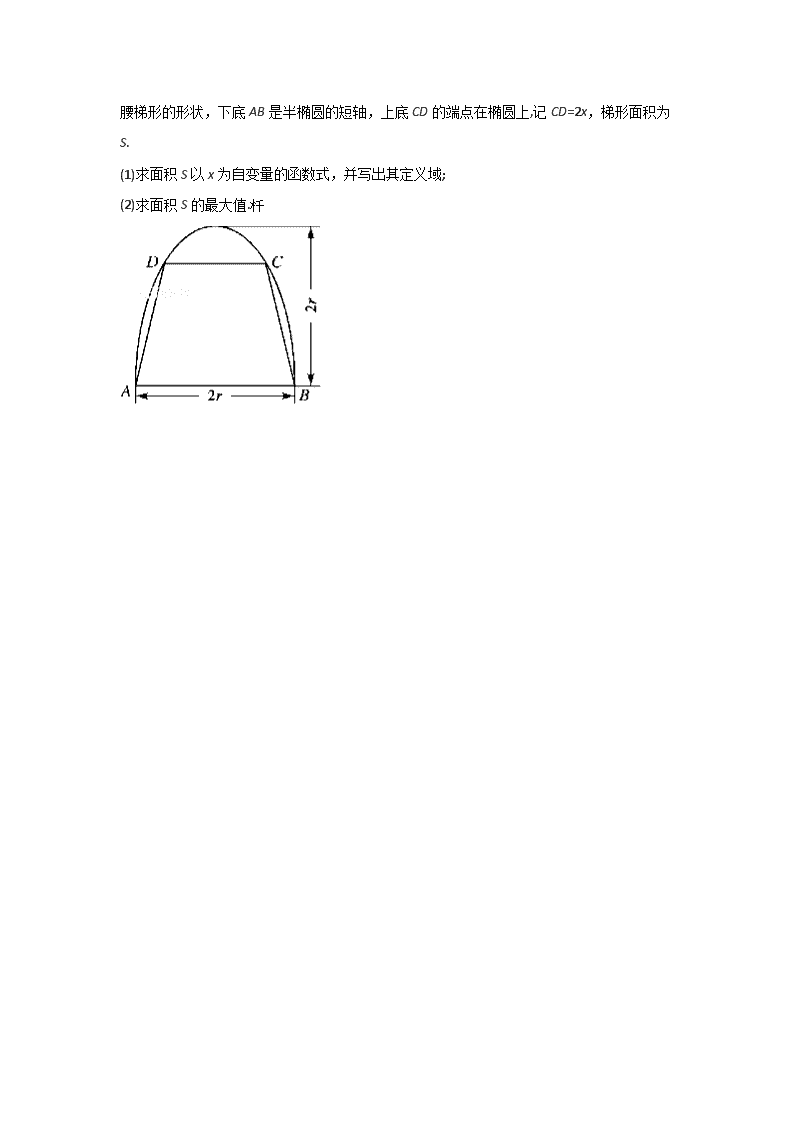
第十四讲 巧用导数解决实际应用问题 题一:现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥,下部分的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的倍. (1)若,,则仓库的容积是多少; (2)若正四棱锥的侧棱长为,当为多少时,仓库的容积最大? 题二:如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r. 计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S. (1)求面积S以x为自变量的函数式,并写出其定义域; (2)求面积S的最大值. 巧用导数解决实际应用问题 题一:(1);(2); 题二:(1),定义域为;(2).查看更多