高中数学北师大版新教材必修一同步课件:阶段提升课 第四课 指数函数、对数函数与函数的应用
阶段复习课
第四课 指数函数、对数函数与函数的应用
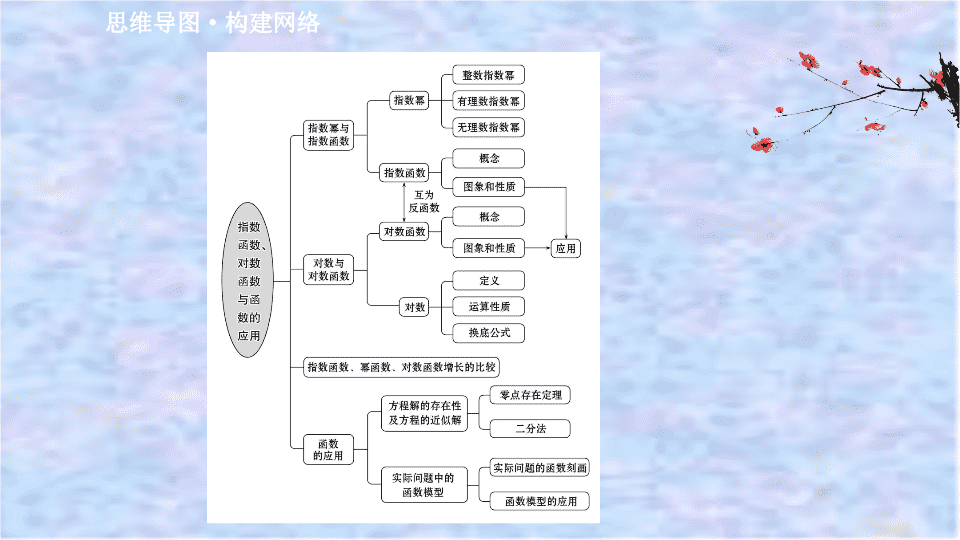
思维导图
·
构建网络
考点整合
·
素养提升
题组训练一 指数幂与指数的运算
1.
下列说法正确的个数是
(
)
(1)49
的平方根为
7;(2)
(3) (4)
A.1 B.2 C.3 D.4
【
解析
】
选
A.49
的平方根是
±7,(1)
错
;(2)
显然正确
; =a
5
b
-5
,(3)
错
;
(4)
错
.
2.
计算
: =
.
【
解析
】
答案
:
-
【
方法技巧
】
1.
根式化简与求值的思路及注意点
(1)
思路
:
首先要分清根式为奇次根式还是偶次根式
,
然后运用根式的性质进行
化简
.
(2)
注意点
:①
正确区分
( )
n
与 两式
;
②
运算时注意变式、整体代换
,
以及平方差、立方差和完全平方、完全立方公
式的运用
,
必要时要进行讨论
.
2.
计算时
,
通常会把根式转化成分数指数幂的形式
,
然后利用有理数指数幂的运
算性质解题
.
题组训练二 指数函数
1.
已知
a= ,b=π
0
,c=3
0.9
,
则
a,b,c
的大小关系是
(
)
A.c
3,
即有
a>c>b,
即
b0,
则向左平移
a
个单位
;
若
a<0,
则向右平移
-a
个单位
.
图象平移的基本方法
:
上加下减
,
左加右减
.
(2)
指数式题目比较大小的方法
:
当两个指数底数相同时
,
利用指数函数的单调性直接比较大小
;
当两个数不能利用同一函数的单调性作比较时
,
可考虑引入中间量
,
常用的中间量有
0
和
±1.
题组训练三 对数与对数的运算
1.
化简
log
6
12-2log
6
的结果为
(
)
【
解析
】
选
C.
原式
=
lo
g
6
-
lo
g
6
2=
lo
g
6
=
lo
g
6
.
2.
已知
2
x
=5
y
=t, =2,
则
t= (
)
A. B. C. D.100
【
解析
】
选
C.
因为
2
x
=5
y
=t>0,t≠1,
所以
x= ,y= .
代入
=2,
所以
+ =2,
所以
ln 10=ln t
2
,
所以
t
2
=10,
则
t= .
【
方法技巧
】
1.
对数化简基本原则
对数式的化简求值一般是正用或逆用公式
,
对真数进行处理
,
选哪种策略化简
,
取决于问题的实际情况
,
一般本着便于真数化简的原则进行
.
2.
应用换底公式应注意的两个方面
(1)
化成同底的对数时
,
要注意换底公式的正用、逆用以及变形应用
.
(2)
题目中有指数式和对数式时
,
要注意将指数式与对数式统一成一种形式
.
题组训练四 对数函数
1.
已知实数
a=log
4
5,b= ,c=log
3
0.4,
则
a,b,c
的大小关系为
(
)
A.b1,b= ∈(0,1),c=
lo
g
3
0.4<0,
故
c0
且
a≠1),
设
h(x)=
f(x)-g(x).
(1)
求函数
h(x)
的定义域
,
判断
h(x)
的奇偶性
,
并说明理由
;
(2)
若
f(3)=2,
求使
h(x)<0
成立的
x
的集合
.
【
解析
】
(1)
因为
f(x)=log
a
(1+x)
的定义域为
{x|x>-1},
g(x)=log
a
(1-x)
的定义域为
{x|x<1},
所以
h(x)=f(x)-g(x)
的定义域为
{x|x>-1}∩{x|x<1}={x|-10,
且函数
f(x)
在
(0,+∞)
上单调递增
,
所以函数的零点所在区间为
(1,2).
2.
在
26
枚崭新的金币中
,
有一枚外表与真金币完全相同的假币
(
质量小一点
),
现在只有一架天平
,
则应用二分法的思想
,
最多称
次就可以发现这枚假币
.
【
解析
】
将
26
枚金币平均分成两份
,
分别放在天平两端
,
则假币一定在质量小的那
13
枚金币里面
.
从这
13
枚金币中拿出
1
枚
,
然后将剩下的
12
枚金币平均分成两份
,
分别放在天平两端
,
若天平平衡
,
则假币一定是拿出的那一枚
;
若不平衡
,
则假币一定在质量小的那
6
枚金币里面
,
将这
6
枚金币平均分成两份
,
分别放在天平两端
,
则假币一定在质量小的那
3
枚金币里面
,
从这
3
枚金币中任拿出
2
枚
,
分别放在天平两端
,
若天平平衡
,
则剩下的那一枚是假币
,
若不平衡
,
则质量小的那一枚是假币
.
综上可知
,
最多称
4
次就可以发现这枚假币
.
答案
:
4
【
方法技巧
】
(1)
判断零点所在区间有两种方法
:
一是利用零点存在定理
,
二是利用函数图象
.
(2)
二分法思想在实际问题中有许多的应用
,
通过巧妙取区间、巧妙分析和缩小区间
,
从而以最短的时间和最小的精力达到目的
.