【数学】2014高考专题复习：第8章 立体几何 第1节空间几何体的结构、三视图和直观图、表面积和体积

【数学】2014高考专题复习：第8章 立体几何 第1节空间几何体的结构、三视图和直观图、表面积和体积

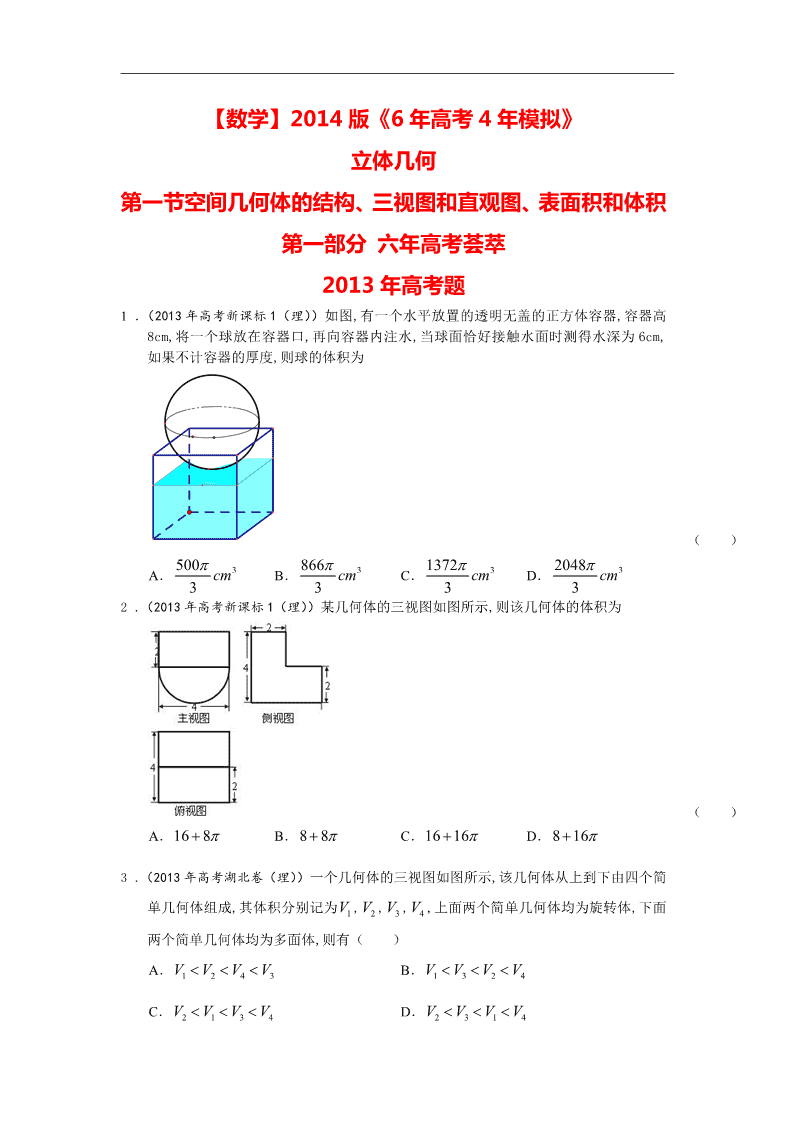
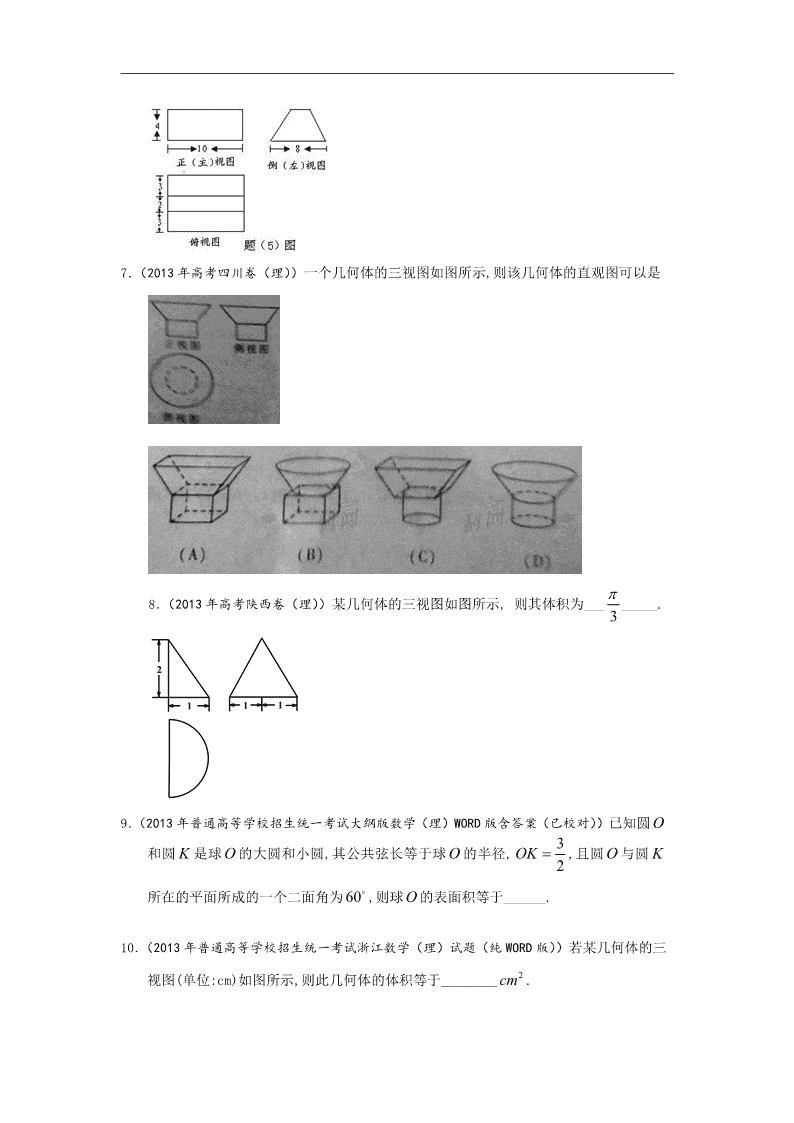
‎【数学】2014版《6年高考4年模拟》‎ 立体几何 第一节空间几何体的结构、三视图和直观图、表面积和体积 第一部分 六年高考荟萃 ‎2013年高考题 ．（2013年高考新课标1（理））如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为 ‎ ‎ （　　）‎ A． B． C． D．‎ ．（2013年高考新课标1（理））某几何体的三视图如图所示,则该几何体的体积为 ‎ （　　）‎ A． B． C． D．‎ ．（2013年高考湖北卷（理））一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为,,,,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有（　　）‎ A． B． ‎ C． D．‎ ‎ ‎ ．（2013年高考湖南卷（理））已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于 （　　）‎ A． B． C． D． ‎ ．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））某四棱台的三视图如图所示,则该四棱台的体积是 ‎ 正视图 俯视图 侧视图 第5题图 ‎ （　　）‎ A． B． C． D．‎ ．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））某几何体的三视图如题图所示,则该几何体的体积为 （　　）‎ A． B． C． D．‎ ．（2013年高考四川卷（理））一个几何体的三视图如图所示,则该几何体的直观图可以是 ‎ ‎ ‎ ．（2013年高考陕西卷（理））某几何体的三视图如图所示, 则其体积为________.‎ ．（2013年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,,且圆与圆所在的平面所成的一个二面角为,则球的表面积等于______.‎ ．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________.‎ ‎4‎ ‎3‎ ‎2‎ ‎3‎ ‎3‎ 正视图 侧视图 俯视图 ‎（第12题图）‎ ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））某几何体的三视图如图所示,则该几何体的体积是____________.‎ ．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD版））已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________‎ ‎2012年高考题 ‎1.[2012·重庆卷] 设四面体的六条棱的长分别为1,1,1,1，和a，且长为a的棱与长为的棱异面，则a的取值范围是(　　)‎ A．(0，) B．(0，)C．(1，) D．(1，)‎ ‎2. [2012·辽宁卷] 一个几何体的三视图如图所示．则该几何体的表面积为________．‎ ‎3.[2012·北京卷] 某三棱锥的三视图如图1－4所示，该三棱锥的表面积是(　　)‎ A．28＋6 B．30＋6 C．56＋12 D．60＋12 ‎4.[2012·安徽卷] 某几何体的三视图如图1－3所示，该几何体的表面积是________．‎ 图1－3‎ ‎5. [2012·天津卷] 一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m3.‎ ‎6.[2012·福建卷] 一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是(　　)‎ A．球 B．三棱锥C．正方体 D．圆柱 ‎7. [2012·广东卷] 某几何体的三视图如图所示，它的体积为(　　)‎ A．12π B．45πC．57π D．81π ‎8. [2012·湖北卷] 已知某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A. B．3πC. D．6π ‎9.[2012·湖南卷] 某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是(　　)‎ ‎10. [2012·课标全国卷] 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为(　　)‎ A．6 B．9 C．12 D．18‎ ‎11.[2012·浙江卷] 已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积等于 ‎________cm3.‎ ‎2011年高考题 ‎1. (2011年高考山东卷理科11)‎ 下图是长和宽分别相等的两个矩形．给定下列三个命题：‎ ‎①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是 ‎(A)3 (B)2 (C)1 (D)0‎ ‎2.(2011年高考浙江卷理科3)若某几何体的三视图如图所示，则这个几何体的直观图可以是 ‎4.(2011年高考安徽卷理科6)一个空间几何体得三视图如图所示，则该几何体的表面积为 ‎ ‎ ‎ （A） 48 (B)32+8 (C) 48+8 (D) 80‎ ‎5.(2011年高考辽宁卷理科12)已知球的直径SC=4，A,B是该球球面上的两点，AB=，，则棱锥S-ABC的体积为（ ）‎ ‎（A） （B） （C） （D）1‎ ‎10.(2011年高考广东卷理科7)如图．某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为（ ）‎ ‎ A. B. C. D.‎ ‎11.(2011年高考陕西卷理科5)某几何体的三视图如图所示，则它的体积是 ‎ ‎ （A）（B） ‎ ‎（C）（D）‎ ‎15. (2011年高考全国卷理科11)已知平面截一球面得圆M，过圆心M且与成，二面角的平面 截该球面得圆N，若该球的半径为4，圆M的面积为4，则圆N的面积为 ‎ (A) (B) (c) (D)‎ ‎16．(2011年高考北京卷理科7)某四面体的三视图如图所示，该四面体四个面的面积中，最大的是 ‎ A．8 B． C．10 D．‎ ‎1.(2011年高考辽宁卷理科15)一个正三棱柱的侧棱长和底面边长相等，体积为，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是____________.‎ ‎2. (2011年高考全国新课标卷理科15)已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为 。‎ ‎3．(2011年高考天津卷理科10)一个几何体的三视图如图所示（单位：），则这个几何体的体积为__________ ‎ ‎4. (2011年高考四川卷理科15)如图，半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时，求球的表面积与该圆柱的侧面积之差是 . ‎ ‎6．(2011年高考福建卷理科12)三棱锥P-ABC中，PA⊥底面ABC，PA=3，底面ABC是边长为2的正三角形，则三棱锥P-ABC的体积等于______。‎ ‎7．(2011年高考上海卷理科7)若圆锥的侧面积为，底面积为，则该圆锥的体积为 。‎ 三、解答题:‎ ‎1. (2011年高考山东卷理科19)（本小题满分12分）‎ 在如图所示的几何体中，四边形ABCD为平行四边形，∠ ACB=，ＥＡ⊥平面ＡＢＣＤ，EF∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ.‎ ‎（Ⅰ)若Ｍ是线段ＡＤ的中点，求证：ＧＭ∥平面ＡＢＦＥ;‎ ‎（Ⅱ）若ＡＣ＝ＢＣ=２ＡＥ,求二面角Ａ-ＢＦ-Ｃ的大小．‎ ‎2010年高考题 一、选择题 ‎1.（2010全国卷2理）（9）已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为 ‎（A）1 （B） （C）2 （D）3‎ ‎2.（2010陕西文） 8.若某空间几何体的三视图如图所示，则该几何体的体积是 [B]‎ ‎ （A）2 （B）1 ‎ ‎（C） （D）‎ ‎3.（2010辽宁文）（11）已知是球表面上的点，，，‎ ‎，，则球的表面积等于 ‎（A）4 （B）3 （C）2 （D）‎ ‎4.（2010安徽文）（9）一个几何体的三视图如图，该几何体的表面积是 ‎（A）372 （B）360 ‎ ‎（C）292 （D）280‎ ‎.‎ ‎5.（2010重庆文）（9）到两互相垂直的异面直线的距离相等的点 ‎（A）只有1个 （B）恰有3个 ‎（C）恰有4个 （D）有无穷多个 ‎6.（2010浙江文）‎ ‎（8）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是 ‎（A）cm3 ‎ ‎（B）cm3‎ ‎（C）cm3 ‎ ‎（D）cm3‎ ‎7.（2010北京文）（8）如图，正方体的棱长为2，动点E、F在棱上。点Q是CD的中点，动点 P在棱AD上，若EF=1，DP=x，E=y(x,y大于零)，‎ 则三棱锥P-EFQ的体积：‎ ‎（A）与x，y都有关； （B）与x，y都无关；‎ ‎（C）与x有关，与y无关； （D）与y有关，与x无关；‎ ‎8.（2010北京文）（5）一个长方体去掉一个小长方体，所得几何体的 正（主）视图与侧（左）视图分别如右图所示，则该 集合体的俯视图为：‎ ‎ ‎ ‎9.（2010北京理）(8)如图，正方体ABCD-的棱长为2，动点E、F在棱上，动点P，Q分别在棱AD，CD上，若EF=1，E=x，DQ=y，DＰ＝ｚ（ｘ，ｙ，ｚ大于零），则四面体PEＦＱ的体积　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎　　　（Ａ）与ｘ，ｙ，ｚ都有关 ‎　　　（Ｂ）与ｘ有关，与ｙ，ｚ无关 ‎　　　（Ｃ）与ｙ有关，与ｘ，ｚ无关 ‎　　　（Ｄ）与ｚ有关，与ｘ，ｙ无关 ‎10.（2010北京理）（3）一 个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为 ‎ ‎ ‎ ‎11.（2010广东理）6.如图1，△ ABC为三角形，// // ,  ⊥平面ABC 且3== =AB,则多面体△ABC -的正视图（也称主视图）是 ‎12.（2010广东文）‎ ‎13.（2010福建文）3．若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )‎ A． B．2 ‎ C． D．6‎ ‎14.（2010全国卷1文）‎ ‎（12）已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2,则四面体ABCD的体积的最大值为 ‎(A) (B) (C) (D) ‎ 二、填空题 ‎1.（2010上海文）6.已知四棱椎的底面是边长为6 的正方形，侧棱底面，且，则该四棱椎的体积是 。‎ ‎2.（2010湖南文）13.图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm ‎3.（2010浙江理）（12）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是___________.‎ ‎4.（2010辽宁文）（16）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的 长为 .‎ ‎5.（2010辽宁理）（15）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.‎ ‎6.（2010天津文）（12）一个几何体的三视图如图所示，则这个几何体的体积为 。‎ ‎7.（2010天津理）（12）一个几何体的三视图如图所示，则这个几何体的体积为 ‎ 三、解答题 ‎1.（2010上海文）20.（本大题满分14分）本题共有2个小题，第1小题满分7分，第2‎ 小题满分7分.‎ 如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用平方米塑料片制成圆柱的侧面和下底面（不安装上底面）.‎ ‎(1)当圆柱底面半径取何值时，取得最大值？并求出该 最大值（结果精确到0.01平方米）;‎ ‎(2)若要制作一个如图放置的，底面半径为0.3米的灯笼，请作出 用于灯笼的三视图（作图时，不需考虑骨架等因素）. ‎ ‎2.（2010陕西文）18.(本小题满分12分)‎ 如图，在四棱锥P—ABCD中，底面ABCD是矩形PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.‎ ‎ (Ⅰ)证明：EF∥平面PAD；‎ ‎ (Ⅱ)求三棱锥E—ABC的体积V.‎ ‎ ‎ ‎ ‎ ‎3.（2010安徽文）19.(本小题满分13分)‎ 如图，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB,EF⊥FB,∠BFC=90°，BF=FC,H为BC的中点，‎ ‎(Ⅰ)求证：FH∥平面EDB;‎ ‎（Ⅱ）求证：AC⊥平面EDB; ‎ ‎（Ⅲ）求四面体B—DEF的体积；‎ ‎4.（2010四川理）（18）（本小题满分12分）‎ 已知正方体ABCD－A'B'C'D'的棱长为1，点M是棱AA'的中点，点O是对角线BD'的中点.‎ ‎（Ⅰ）求证：OM为异面直线AA'和BD'的公垂线；‎ ‎（Ⅱ）求二面角M－BC'－B'的大小；‎ ‎（Ⅲ）求三棱锥M－OBC的体积. ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ ‎2009年高考题 ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ 一、选择题 ‎1. 一空间几何体的三视图如图所示,则该几何体的体积为( ).‎ A. B. ‎ ‎ C. D. ‎ ‎2.一个棱锥的三视图如图，则该棱锥的全面积（单位：c）为 ‎（A）48+12 （B）48+24 （C）36+12 （D）36+24‎ ‎3.正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥P-GAC体积之比为 ‎（A）1：1 (B) 1：2 (C) 2：1 (D) 3：2‎ ‎4.在区间[-1，1]上随机取一个数x，的值介于0到之间的概率为( ).‎ A. B. C. D. ‎ ‎5. 如右图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为。则该集合体的俯视图可以是 ‎6.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现有沿该正方体的一些棱将正方体剪开、外面朝上展平，得到右侧的平面图形，则标“”‎ 的面的方位是 A. 南 B. 北 ‎ C. 西 D. 下 ‎7.如图，在半径为3的球面上有三点，， ‎ 球心到平面的距离是，则两点的球面距离是 A. B. C. D. ‎ ‎8．若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为 ‎ A. B. C. D. ‎ ‎9，如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的主视图是（ ）‎ 二、填空题 ‎10..图是一个几何体的三视图，若它的体积是，则a=_______‎ ‎11.如图是一个几何体的三视图，若它的体积是，则__________‎ ‎12．若某几何体的三视图（单位：）如图所示，则此几何体的体积是 ‎ ‎．‎ ‎13.设某几何体的三视图如下（尺寸的长度单位为m）。 ‎ ‎ 则该几何体的体积为 ‎ ‎14. 直三棱柱的各顶点都在同一球面上，若 ‎,，则此球的表面积等于 。 ‎ ‎15．正三棱柱内接于半径为的球，若两点的球面距离为，则正三棱柱的体积为 　　．‎ ‎16．体积为的一个正方体，其全面积与球的表面积相等，则球的体积等于 ．‎ ‎17．如图球O的半径为2，圆是一小圆，，A、B 是圆上两点，若A，B两点间的球面距离为，则= .‎ ‎18.已知三个球的半径，，满足，则它们的表面积，，，‎ 满足的等量关系是___________. ‎ ‎19.若球O1、O2表示面积之比，则它们的半径之比=_____________.‎ 三、解答题 ‎20．（本小题满分13分）‎ ‎ 某高速公路收费站入口处的安全标识墩如图4所示。墩的上半部分是正四棱锥 ‎，下半部分是长方体。图5、图6分别是该标识墩的正（主）视图和俯视图。‎ ‎（1）请画出该安全标识墩的侧（左）视图； ‎ ‎（2）求该安全标识墩的体积；‎ ‎（3）证明：直线平面.‎ ‎ ‎ ‎2008年高考题 一、选择题 ‎1.(2008广东）将正三棱柱截去三个角（如图1所示分别是三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）‎ E F D I A H G B C E F D A B C 侧视 图1‎ 图2‎ B E A．‎ B E B．‎ B E C．‎ B E D．‎ ‎2.（2008海南、宁夏理）某几何体的一条棱长为，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为（ ）‎ A． B． C． D．‎ ‎3.（2008山东）下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 A.9π　　　　　 B.10π C.11π D．12π ‎3. (2007宁夏理•8) 已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）‎ ‎10‎ ‎20 ‎ ‎10‎ ‎20 ‎ ‎20 ‎ ‎20 ‎ 俯视图 侧视图 正视图 Ａ． Ｂ． Ｃ． Ｄ．‎ ‎4. （2007陕西理•6）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）‎ A． B． C． D． ‎ 二、填空题 ‎11.（2008海南、宁夏理科）一个六棱柱的底面是正六边 ‎ 形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为3，则这个球的体积为　　　　　　． ‎ ‎12.（2008海南、宁夏文）一个六棱柱的底面是正六边形，其侧棱垂直底面。已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为，底面周长为3，那么这个球的体积为_________‎ 第二部分 四年联考汇编 ‎2013-2014年联考题 一．基础题组 ‎1.【2014福建南安】下列图形中不一定是平面图形的是（ ）‎ A. 三角形 B. 四边相等的四边形 C. 梯形 D.平行四边形 ‎2.【2014年“皖西七校”高三年级联合考试】一个几何体按比例绘制的三视图如右图所示（单位:），‎ 则该几何体的体积为（ ）‎ A. B. C. D. ‎ ‎3.【2014年“皖西七校”高三年级联合考试】已知是两个不同的平面，下列四个条件中能推出的是（ ）‎ ‎①存在一条直线； ②存在一个平面；‎ ‎③存在两条平行直线；‎ ‎④存在两条异面直线.‎ A.①③ B.②④ C.①④ D.②③‎ ‎4.【2014福建南安】如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）‎ A． B．‎ ‎ C． D．‎ ‎5.【2014福建南安】的斜二侧直观图如图所示，则的面积为（ ）‎ A． B． C． D．‎ ‎6.【2014安徽涡阳蒙城】 如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（ ）‎ A．三棱台、三棱柱、圆锥、圆台 B．三棱台、三棱锥、圆锥、圆台 C．三棱柱、正四棱锥、圆锥、圆台 D．三棱柱、三棱台、圆锥、圆台 ‎7.【2014年“皖西七校”高三年级联合考试】在三棱锥中，，，，则与平面所成角的余弦值为 .‎ ‎8.【2014福建南安】已知一个球的表面积为，则这个球的体积为 。‎ ‎9.【2014福建南安】若某空间几何体的三视图如图所示，则该几何体的体积是_ 。‎ ‎10. 一个几何体的三视图如图所示，已知这个几何体的体积为，则h________.‎ 二．能力题组 ‎11.【2014福建南安】设是两条不同的直线，是三个不同的平面，给出下列四个命题：‎ ‎①若，，则 ②若，，，则 ‎③若，，，则 ④若，，，则 正确命题的个数是( )‎ A．1 B．2 C．3 D．4‎ ‎12.【2014安徽省六校教育研究会高三2月联考数学理】某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是（ ）‎ ‎（A） （B） (C) (D) ‎ ‎13.【2014安徽涡阳蒙城】设m、n是两条不同的直线，是三个不同的平面，给出下列四个命题：‎ ‎①若，，则 ②若，，，则 ‎③若，，则 ④若，，则 其中正确命题的序号是 ( )‎ A.①和② B.②和③ C.③和④ D.①和④‎ ‎14.【2014安徽涡阳蒙城】等腰梯形，上底，腰，下底，以下底所在直线为x轴，则由斜二测画法画出的直观图的面积为_______．‎ ‎15.【2014安徽涡阳蒙城】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)长方形;(3)正方形;(4)正六边形.其中正确的结论是____________.(把你认为正确的序号都填上)‎ ‎16.【2014福建南安】（本小题满分12分）‎ 如图，在三棱锥中，分别为的中点.‎ ‎（1）求证：EF∥平面;‎ ‎（2）若平面平面，且，º，求证：平面平面 ‎ ‎17.【2014福建南安】（本小题满分12分）‎ 如图，在四棱锥中，平面，底面为直角梯形，∥，‎ ‎，,‎ ‎（1）求证： ⊥平面；‎ ‎（2）求异面直线与所成角的大小。‎ ‎18.【2014福建南安】如图，将边长为的正方形沿对角线折起，使得平面平面，在折起后形成的三棱锥中，给出下列三个命题：‎ ‎①是等边三角形； ②； ③三棱锥的体积是；④AB与CD所成的角是60°。其中正确命题的序号是 ．（写出所有正确命题的序号）‎ ‎19. 【2014福建安溪八中12月月考数学理】（本小题满分13分）如图，四棱锥中，侧面是边长为2的正三角形，且与底面垂直，底面是的菱形，为的中点.(Ⅰ)求与底面所成角的大小；(Ⅱ)求证：平面；(Ⅲ)求二面角的余弦值. ‎ ‎20.【2014安徽省六校教育研究会高三2月联考数学理】（本小题满分12分）‎ 等边三角形的边长为3,点、分别是边、上的点,且满足 ‎(如图1).将△沿折起到△的位置,使二面角为直二面角,连结、 (如图2).‎ ‎（Ⅰ）求证:平面;‎ ‎（Ⅱ）在线段上是否存在点,使直线与平面所成的角为?若存在,求出的长,若不存在,请说明理由.‎ ‎21.【2014安徽涡阳蒙城】（满分13分）‎ 在正方体中，、为棱、的中点．‎ ‎（1）求证：∥平面；‎ ‎（2）求证：平面⊥平面 ‎ ‎ 三．拔高题组 ‎22.【2014宿州一模】四棱锥P-ABCD中,底面ABCD是平行四边形, ,,若平面BDE,则的值为 ( )‎ ‎ A.1 B.3 C.2 D.4‎ ‎23.【2014年“皖西七校”高三年级联合考试】（本小题满分12分）如图1，已知的直径，点、为上两点，且，，为弧的中点．将沿直径折起，使两个半圆所在平面互相垂直（如图2）．‎ ‎（①）求证：；‎ ‎（②）在弧上是否存在点，使得平面？若存在，试指出点的位置；若不存在，请说明理由；‎ ‎（③）求二面角的正弦值.‎ ‎24.【2014福建南安】（本小题满分12分）如图，在四棱锥中，是正方形，平面，， 分别是的中点．‎ ‎（1）在线段上确定一点，使平面，并给出证明；‎ ‎（2）证明平面平面，并求出到平面的距离.‎ ‎25.【2014宿州一模】（本小题满分12分）如图，四边形PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD, ∠BAD=∠ADC=90°,AB=AD=.‎ ‎(Ⅰ)若M为PA中点,求证:AC∥平面MDE;‎ ‎(Ⅱ)求平面PAD与PBC所成锐二面角的大小.‎ ‎2012-2013年联考题 ‎1【云南省玉溪一中2013届高三上学期期中考试理】一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的 等腰直角三角形，则该几何体的外接球的表面积为（ ）‎ A. B. C. D.‎ ‎2.【云南省玉溪一中2013届高三上学期期中考试理】设表示不同的直线，表示不同的平面，给出下列四个命题： ‎ ‎ ①若∥，且则； ②若∥，且∥.则∥；‎ ‎ ③若，则∥m∥n； ‎ ‎ ④若且n∥,则∥m.‎ ‎ 其中正确命题的个数是( )‎ ‎ A．1 B．2 C．3 D．4‎ ‎3.【云南师大附中2013届高三高考适应性月考卷（三）理科】一个几何体的三视图如图l所示，其中正视图是一个正三角形，则该几何体的体积为 （ ） ‎ ‎ A．1 B． C． D． ‎ ‎4.【云南省玉溪一中2013届高三第三次月考 理】已知三棱锥的三视图如图所示，则它的外接球表面积为（ ）‎ ‎ A．16 B．4 C．8 D．2‎ ‎5.【云南省昆明一中2013届高三新课程第一次摸底测试理】如图， 在长方体ABCD—A1B1C1D1中，对角线B1D与平面A1BC1相交于点E，则点E为△A1BC1的 ‎ A．垂心 B．内心 C．外心 D．重心 ‎6.【云南省昆明一中2013届高三新课程第一次摸底测试理】某几何体的三视图如图所示，则该几何体的表面积为 ‎ A． B．‎ ‎ C． D．32‎ ‎7.【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】设b，c表示两条直线，表示两个平面，则下列命题正确的是 A.若 B.若 C.若 D.若 ‎8.【山东省聊城市东阿一中2013届高三上学期期初考试 】设直线m、n和平面,下列四个命题中，正确的是 （ ）‎ ‎ A. 若 B. 若 ‎ C. 若 D. 若 ‎9.【北京市东城区普通校2013届高三12月联考数学（理）】 已知是两条不同直线，是三个不同平面，下列命题中正确的是 ‎ A． B． ‎ ‎ C． D． ‎ ‎10.【北京市东城区普通校2013届高三12月联考数学（理）】一个棱锥的三视图如图（尺寸的长度单位为）， 则该棱锥的体积是 ‎ A． B． C． D． ‎ ‎10.【云南省玉溪一中2013届高三第三次月考 理】设动点在棱长为1的正方体的对角线上，记。当为钝角时，则的取值范围是 。‎ ‎11.【云南省玉溪一中2013届高三第四次月考理】已知正三棱锥，点 都在半径为的球面上，若两两互相垂直，则球心到截面的距离为________.‎ ‎12.【云南师大附中2013届高三高考适应性月考卷（三）理科】正三棱锥A－BCD内接于球O，且底面边长为，侧棱长为2，则球O的表面积为____ ．‎ ‎13.【山东省济南外国语学校2013届高三上学期期中考试 理科】一个几何体的三视图如图所示(单位:m),则该几何体的体积为 .‎ ‎14.【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】一个几何体的三视图如右图所示，则该几何体的表面积为__________.‎ ‎15.【天津市新华中学2012届高三上学期第二次月考理】 如图为一个几何体的三视图，其中俯视为正三角形，AB=2,AA=4，则该几何体的表面积为_______。‎ ‎ ‎ ‎16.【云南省玉溪一中2013届高三第三次月考 理】（本小题满分12分）如图，在长方体，中，，点在棱AB上移动.‎ ‎（1）证明：； ‎ ‎（2）当为的中点时，求点到面的距离； ‎ ‎（3）等于何值时，二面角的大小为.‎ ‎17.【云南省玉溪一中2013届高三第四次月考理】（本题12分）如图6，在长方体中，，为中点.‎ ‎（1）求证：；‎ ‎（2）在棱上是否存在一点，使得平面?若存在，求的长；若不存在，说明理由；‎ ‎（3）若二面角的大小为30°，求的长. ‎ ‎ ‎ ‎ 图6‎ ‎ ‎ ‎18.【云南师大附中2013届高三高考适应性月考卷（三）理科】（本小题满分12分）‎ ‎ 如图5甲，四边形ABCD中，E是BC的中点，DB =2, DC=1，BC=，AB =AD=‎ ‎．将（图甲）沿直线BD折起，使二面角A － BD －C为60o（如图乙）． ‎ ‎ （Ⅰ）求证：AE⊥平面BDC;‎ ‎ （Ⅱ）求点B到平面ACD的距离．‎ ‎19.【北京市东城区普通校2013届高三12月联考数学（理）】（本小题满分分）‎ ‎ 已知：如图，在四棱锥中，四边形为正方形，，且，为中点．‎ ‎（Ⅰ）证明：//平面；‎ ‎（Ⅱ）证明：平面平面；‎ ‎（Ⅲ）求二面角的正弦值．‎ ‎20.【云南省玉溪一中2013届高三上学期期中考试理】（本小题满分12分）‎ ‎ 在直三棱柱中， ∠ACB=90°,Ｍ是 的中点，Ｎ是的中点 ‎ （Ⅰ）求证：MN∥平面 ；‎ ‎ （Ⅱ）求点到平面BMC的距离； ‎ ‎ （Ⅲ）求二面角的平面角的余弦值大小。‎ ‎21.【山东省烟台市莱州一中20l3届高三第二次质量检测 （理）】（本题满分12分）‎ 如图1，平面四边形ABCD关于直线AC对称，‎ 折起（如图2），使二面角A-BD-C的余弦值等于 ‎.对于图2，完成以下各小题：‎ ‎（1）求A，C两点间的距离；‎ ‎（2）证明：AC⊥平面BCD；‎ ‎（3）求直线AC与平面ABD所成角的正弦值.‎ ‎22.【天津市耀华中学2013届高三第一次月考理科】‎ ‎(本小题满分13分)在如图所示的多面体中，EF平面AEB，AEEB，AD//EF，‎ EF//BC．BC=2AD=4，EF=3，AE=BE=2，G为BC的中点。‎ ‎ (1)求证：AB//平面DEG；‎ ‎ (2)求证：BDEG；‎ ‎ (3)求二面角C—DF—E的正弦值。‎ ‎23.【山东省济南外国语学校2013届高三上学期期中考试 理科】（本小题满分12分）‎ 如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。‎ Ⅰ、求证：CE⊥平面PAD；‎ Ⅱ、若PA=AB=1，AD=3，CD=，∠CDA=45°， ‎ 求四棱锥P-ABCD的体积.‎ Ⅲ、在满足（Ⅱ）的条件下求二面角B-PC-D的 余弦值的绝对值.‎ ‎24.【山东省聊城市东阿一中2013届高三上学期期初考试 】本小题满分12分）如图，直角梯形与等腰直角三角形所在的平面互相垂直．∥，，，．‎ ‎（1）求证：；‎ ‎（2）求直线与平面所成角的正弦值； ‎ ‎（3）线段上是否存在点，使// 平面？若存在，求出；若不存在，说明理由． ‎ ‎2011-2012年联考题 ‎1、（2012莱芜一中模拟）设、是不同的直线，、、是不同的平面，有以下四个命题：‎ ‎（1）（2）（3）（4），其中正确的是 ‎ ‎(A)（1）（2） (B)（1）（3）　 (C)（2）（3） (D)（2）（4） ‎ ‎2、（2012德州一模）对于直线和平面，有如下四个命题：‎ ‎ (1)若m∥，mn，则n (2)若m，mn，则n∥‎ ‎ (3)若，,则∥ (4)若m，m∥n，n，则 ‎ 其中真命题的个数是()‎ ‎ A．1 B．2 C．3 D．4‎ ‎3、（2012临沂3月模拟）一个三棱柱的正（主）视图和侧（左）视图分别是矩形和正三角形，如图所示，则这个三棱柱的体积为_________； ‎ ‎ ‎ ‎4、（2012滨州二模）某几何体的三视图如图所示，且该几何体的体积是，则正视图中x的值是　‎ ‎（A）2　‎ ‎（B）　‎ ‎（C）　‎ ‎（D）3‎ ‎6、（2012济南3月模拟）如图，正三棱柱ABC-的各棱长均为2，其正（主）视图如图所示，则此三棱柱侧（左）视图的面积为 A. B. 4 C. D. ‎ ‎7、（2012济南三模）一个几何体的三视图如右图所示，则这个几何体的体积等于( )‎ ‎ A． B． C． D． ‎ ‎ ‎ ‎8、（2012临沂二模）如下图，某几何体的正视图与侧视图都是边长为1的正方形，且体积是，则该几何体的俯视图可以是 ‎9、（2012青岛二模）设,是两条不同的直线, ,,是三个不同的平面．有下列四个命题：‎ ‎①若，，，则；‎ ‎②若，，则；‎ ‎③ 若，，，则；‎ ‎④ 若，，，则．‎ 其中错误命题的序号是 A．①③ B．①④ C．②③④ D．②③‎ ‎10、（2012青岛二模）一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的 ‎ ‎ ‎ A.外接球的半径为 B.体积为 ‎ C.表面积为 D.外接球的表面积为 ‎11、（2012青岛3月模拟）已知某棱锥的三视图如右图所示，则该棱锥 的体积为 .‎ 正视图 侧视图 俯视图 ‎12、（2012日照5月模拟）已知正三棱柱的正（主）视图和侧 ‎（左）视图如图所示。设 的中心分别是 ‎，现将此三棱柱绕直线旋转，在旋转过程中对 应的俯视图的面积为S，则S的最大值为 ‎ ‎（A）4 （B）8‎ ‎（C）12 （D）16‎ ‎13、（2012泰安一模）一个棱锥的三视图如图所示，则这个棱锥的体积为 . ‎ ‎14、（2012威海二模）如图，三棱锥底面为正三角形，侧面与底面垂直且,已知其主视图的面积为，则其左视图的面积为 A. B. C. D. ‎ ‎15、（2012烟台二模）某几何体的三视图如右图所示，已知其正视图的周长为6，则该几何体体积的最大值为 A. B. C. D.2‎ ‎16、（2012滨州二模）如图，在四棱锥P－ABCD中，PC⊥底面ABCD，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB= 2AD =2CD =2．E是PB的中点．‎ ‎ （I）求证：平面EAC⊥平面PBC;‎ ‎ （II）若二面角P－AC－E的余弦值为，求直线PA与平面EAC所成角的正弦值．‎ ‎17、（2012德州二模）如图甲，直角梯形ABCD中，AB//CD，，点M、N分别在AB、CD上，且MN⊥AB，MC⊥CB，BC=2，MB=4，现将AMND沿MN折起，使平面AMND与平面MNCB垂直（如图乙。）‎ ‎ （I）求证：DC//平面AMB；‎ ‎ （II）当DN的长为何值时，二面角D—BC—N的大小为60°？‎ ‎18、（2012德州一模）如图，矩形ADEF与梯形ABCD所在的平面互相垂直，ADCD，‎ AB∥CD，AB=AD=1．‎ ‎ CD=2,DE=3，M为CE的中点．‎ ‎ (I)求证：BM∥平面ADEF：‎ ‎ (Ⅱ)求直线DB与平面BEC所成角的正弦值；‎ ‎(Ⅲ)求平面BEC与平面DEC所成锐二面角的余弦值．‎ ‎19、（2012济南3月模拟）如图,在直角梯形ABCP中，AP//BC，AP⊥AB，AB=BC=AP=2，D是AP的中点，E，F，G分别为PC、PD、CB的中点，将△PCD沿CD折起，使得PD⊥平面ABCD. ‎ ‎ (1) 求证：平面PCD⊥平面PAD；‎ ‎(2) 求二面角G-EF-D的大小；‎ ‎(3) 求三棱椎D-PAB的体积.‎ ‎20、（2012济南三模）在斜三棱柱中，侧面，,,,.‎ ‎(1)求证：；‎ ‎(2)在侧棱上确定一点，使得二面角的大小为.‎ ‎ ‎ ‎2010年联考题 题组二（5月份更新）‎ ‎1．（池州市七校元旦调研）在三棱柱中，各棱长相等，侧掕垂直于底面，点是侧面的中心，则与平面所成角的大小是 ( )‎ A． B． C． D．‎ ‎3．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正方体表面相交于．设，，则函数的图象大致是（ ）‎ A B C D M N P A1‎ B1‎ C1‎ D1‎ y x A．‎ O y x B．‎ O y x C．‎ O y x D．‎ O ‎ ‎ ‎4. （三明市三校联考）已知某几何体的三视图如右图所示，则该几何体的体积为 ‎ ‎5.（昆明一中三次月考理）四面体ABCD中，共顶点A 的三条棱两两相互垂直，且其长分别为，若四面体的四个顶点同在一个球面上，则这个球的表面积为　　　　。‎ 答案：‎ ‎6．（池州市七校元旦调研）若某几何体的三视图（单位：）如图所示，则此几何体的体积是 ．‎ 俯视图 正视图 侧视图 ‎7.（哈师大附中、东北师大附中、辽宁省实验中学）一个几何体的三视图如图所示：其中，主视图中大三角形的边长是2的正三角形，俯视图为正六边形，那么该几何体几的体积为 .‎ 主视图 俯视图 左视图 ‎8．（安庆市四校元旦联考）（本题满分14分） 如图，在四棱锥中，ABCD是矩形，，‎ ‎，点是的中点，点在上移动。‎ ‎⑴求三棱锥体积；‎ ‎⑵当点为的中点时，试判断与平面的关系，并说明理由；‎ ‎⑶求证：。‎ ‎9. （哈师大附中、东北师大附中、辽宁省实验中学）如图，在三棱柱中，已知学，，，，，网，侧面，‎ ‎（1）求直线C1B与底面ABC所成角正切值；‎ ‎（2）在棱（不包含端点上确定一点的位置,‎ 使得(要求说明理由).‎ ‎（3）在（2）的条件下,若，求二面角的大小.‎ 题组一（1月份更新）‎ 一、选择题 ‎1.（2009滨州一模）设、是两个不同的平面，为两条不同的直线，命题p：若平面，，，则；命题q：，，，则，则下列命题为真命题的是 （ ）‎ ‎ A．p或q B．p且q　　‎ ‎ C．┐p或q　 D．p且┐q ‎2.（2009玉溪市民族中学第四次月考）若球O的半径为1，点A、B、C在球面上，它们任意两点的球面距离都等于则过A、B、C的小圆面积与球表面积之比为 （ ） A． B． ‎ C． D．‎ ‎3.（2009聊城一模）某个几何体的三视图如图所示，则该几何体的体积是 （ ） ‎ A． B．‎ ‎ C． D．‎ ‎4.（2009临沂一模）一个几何体的三视图及长度数据如图， 则该几何体的表面积与体积分别为 A、 B、 C、 D、‎ ‎5.（2009青岛一模）如右图，一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形，则其体积是 A． B. C． D. ‎ 俯视图 正(主)视图 侧(左)视图 ‎2‎ ‎3‎ ‎2‎ ‎2‎ ‎6.（2009上海闸北区）右图是一个几何体的三视图，根据图中数据，‎ 可得该几何体的表面积是………………………………………（ ）‎ A． B． ‎ C． D．‎ ‎7.（2009泰安一模）一个几何体的三视图如图所示，则这个几何体的 ‎ ‎ 体积等于 ‎ (A) 4 (B) 6‎ ‎ (C) 8 (D)12‎ ‎8.（2009枣庄一模）一个几何体的三视图如右图所示，则该几何体外接球的表面积为 （ ）‎ ‎ A． B．‎ ‎ C． D．以上都不对 ‎ ‎9.（2009番禺一模）一个几何体的三视图如右图所示，其中正视图中△ABC是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为（ ）．‎ ‎ A．12 B． ‎ ‎ C． D．6‎ 二、填空题 理第11题 ‎1.（2009上海八校联考）已知一个球的球心到过球面上A、B、C三点的截面的距离等于此球半径的一半，若，则球的体积为________________。‎ ‎2.（2009上海青浦区）如图，用一平面去截球所得截面的面积为cm2，已知 球心到该截面的距离为1 cm，则该球的体积是 　 cm3.‎ A O C B 第19题图 三、解答题 ‎1.（2009上海普陀区）已知复数，（是虚数单位），且.当实数时，试用列举法表示满足条件的的取值集合.‎ ‎2.（2009上海奉贤区模拟考）在直三棱柱ABC-A1B1C1中,∠ABC=90°, AB=BC=1. ‎ ‎(1)求异面直线B1C1与AC所成角的大小；‎ ‎(2)若直线A1C与平面ABC所成角为45°, ‎ 求三棱锥A1-ABC的体积. ‎ ‎3.（2009冠龙高级中学3月月考）在棱长为2的正方体中，（如图）‎ A B C D A1‎ B1‎ C1‎ F E D1‎ 是棱的中点，是侧面的中心．‎ （1） 求三棱锥的体积；‎ ‎(2)求与底面所成的角的大小．（结果用反三角函数表示）‎ ‎4. (2009闸北区) 如图，在四棱锥中，底面是边长为2的正方形，，，为的中点．‎ ‎（Ⅰ）求四棱锥的体积；‎ ‎（Ⅱ）求异面直线OB与MD所成角的大小．‎ ‎5、（2009东莞一模）如图，在长方体，点E在棱AB上移动，小蚂蚁从点A沿长方体的表面爬到点C1，所爬的最短路程为.‎ ‎ （1）求证：D1E⊥A1D； ‎ ‎（2）求AB的长度；‎ ‎ （3）在线段AB上是否存在点E，使得二面角 ‎。若存在，确定 点E的位置；若不存在，请说明理由.‎