数学卷·2018届陕西省西安中学高二上学期10月月考数学试卷（理科）（重点班） （解析版）

数学卷·2018届陕西省西安中学高二上学期10月月考数学试卷（理科）（重点班） （解析版）

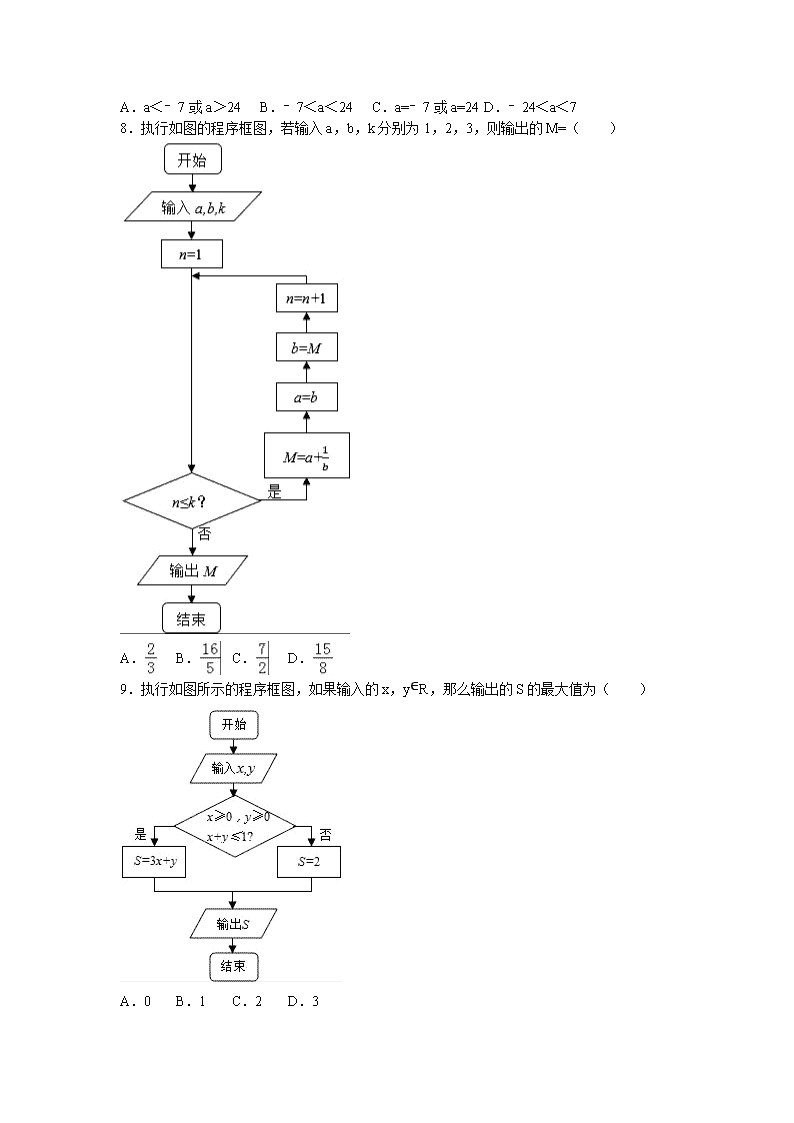
‎2016-2017学年陕西省西安中学高二（上）10月月考数学试卷（理科）（重点班）‎ ‎　‎ 一、选择题（本题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．从装有红球、白球和黑球各2个的口袋内一次取出2个球，则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一白球；③两球至少有一个白球”中的哪几个？（　　）‎ A．①② B．①③ C．②③ D．①②③‎ ‎2．如图是2016年某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的中位数和众数依次为（　　）‎ A．84，84 B．84，85 C．86，84 D．84，86‎ ‎3．将一颗骰子连续抛掷两次，至少出现一次6点向上的概率是（　　）‎ A． B． C． D．‎ ‎4．某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=（　　）‎ A．9 B．10 C．12 D．13‎ ‎5．运行如图算法语句时，执行循环体的次数是（　　）‎ A．25 B．4 C．2 D．5‎ ‎6．设变量x，y满足约束条件：，则z= 的（　　）‎ A．最大值为﹣ B．最小值为﹣ C．最大值为1 D．最小值为1‎ ‎7．点（3，1）和点（﹣4，6）在直线3x﹣2y+a=0两侧，则a的范围是（　　）‎ A．a＜﹣7或a＞24 B．﹣7＜a＜24 C．a=﹣7或a=24 D．﹣24＜a＜7‎ ‎8．执行如图的程序框图，若输入a，b，k分别为1，2，3，则输出的M=（　　）‎ A． B． C． D．‎ ‎9．执行如图所示的程序框图，如果输入的x，y∈R，那么输出的S的最大值为（　　）‎ A．0 B．1 C．2 D．3‎ ‎10．满足条件的区域中共有整点的个数为（　　）‎ A．1 B．2 C．3 D．7‎ ‎11．在用二分法求方程log2x=x的一个近似解时，现在已经将一根锁定在（1，2）内，则下一步可断定该根所在的区间为（　　）‎ A．（1.4，2） B．（1，1.4） C．（1，1.5） D．（1.5，2）‎ ‎12．在某地区某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居众显示可以过正常生活，有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”，根据连续7天的新增病例数计算，下列①～⑤各个选项中，一定符合上述指标的是（　　）‎ ‎①平均数； ‎ ‎②标准差S≤2； ‎ ‎③平均数且标准差S≤2；‎ ‎④平均数且极差小于或等于2；‎ ‎⑤众数等于1且极差小于或等于4．‎ A．①② B．③④ C．③④⑤ D．④⑤‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，满分20分，把正确的答案写在答题纸上指定位置）‎ ‎13．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据（如表），由最小二乘法求得回归方=0.67x+54.9．‎ 零件数x个 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 加工时间y（min）‎ ‎62‎ ‎75‎ ‎81‎ ‎89‎ 现发现表中有一个数据模糊看不清，请你推断出该数据的值为　　．‎ ‎14．如图为一个求20个数的平均数的算法语句，在横线上应填充的语句为　　．‎ ‎15．总体由20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为　　．‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ ‎16．线性约束条件表示平面区域D，若在区域D上有无穷多个点（x，y），可使目标函数z=x+my取得最大值，则m=　　．‎ ‎　‎ 三、解答题（本大题共6小题，满分70分，把正确的答案写在答题纸上指定位置）‎ ‎17．甲、乙两台机床同时加工直径为100 mm的零件，为了检验产品的质量，从产品中各随机抽取6件进行测量，测得数据如下（单位mm）：‎ 甲：99，100，98，100，100，103‎ 乙：99，100，102，99，100，100‎ ‎（1）分别计算上述两组数据的平均数和方差；‎ ‎（2）根据（1）的计算结果，说明哪一台机床加工的这种零件更符合要求．‎ ‎18．某工厂制造A种仪器45台，B种仪器55台，现需用薄钢板给每台仪器配一个外壳．已知钢板有甲、乙两种规格：甲种钢板每张面积2m2，每张可做A种仪器外壳3个和B种仪器外壳5个，乙种钢板每张面积3m2，每张可做A种仪器外壳6个和B种仪器外壳6个．问甲、乙两种钢板各用多少张才能用料最省（“用料最省”是指所用钢板的总面积最小）．‎ ‎19．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的所有数据．‎ B地区用户满意度评分：92，60，69，70，76，82，70，85，72，87，67，50，91，96，70，82，94，85，75，59，74，89，77，88，78，67，79，94，78，65，64，73，60，75，86，65，90，84，74，80‎ ‎（1）完成B地区用户满意度评分的频率分布表并作出频率分布直方图；‎ B地区用户满意度评分的频率分布表 满意度评分分组 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ ‎[90，100）‎ 频数 频率 ‎（2）通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；‎ ‎（3）根据用户满意度评分，将用户的满意度分为三个等级：‎ 满意度评分 低于70分 ‎70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 利用样本近似估计总体的思想方法，估计哪个地区用户的满意度等级为不满意的概率大？说明理由．‎ ‎20．设关于x的一元二次方程x2+2ax+b2=0．‎ ‎（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．‎ ‎（2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．‎ ‎21．某车间为了制定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的 零件的个数x（个）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 加工的时间y（小时）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ 数据如下：‎ ‎（1）在给定的坐标系中画出表中数据的散点图；‎ ‎（2）求出y关于x的线性回归方程=x+，并在坐标系中画出回归直线；‎ ‎（3）试预测加工10个零件需要多少小时？‎ ‎（注： =， =﹣）‎ ‎22．某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：‎ X ‎1‎ ‎2‎ ‎3‎ ‎4‎ Y ‎51‎ ‎48‎ ‎45‎ ‎42‎ 这里，两株作物“相近”是指它们之间的直线距离不超过1米．‎ ‎（1）完成下表，并求所种作物的平均年收获量：‎ Y ‎51‎ ‎48‎ ‎45‎ ‎42‎ 频数 ‎（2）在所种年收获量为51或48的作物中随机选取两株求收获量之和，收获量之和为t的概率．‎ ‎　‎ ‎2016-2017学年陕西省西安中学高二（上）10月月考数学试卷（理科）（重点班）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．从装有红球、白球和黑球各2个的口袋内一次取出2个球，则与事件“两球都为白球”互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一白球；③两球至少有一个白球”中的哪几个？（　　）‎ A．①② B．①③ C．②③ D．①②③‎ ‎【考点】互斥事件与对立事件．‎ ‎【分析】结合互斥事件和对立事件的定义，即可得出结论 ‎【解答】解：根据题意，结合互斥事件、对立事件的定义可得，事件“两球都为白球”和事件“两球都不是白球”；事件“两球都为白球”和事件“两球中恰有一白球”；不可能同时发生，故它们是互斥事件．‎ 但这两个事件不是对立事件，因为他们的和事件不是必然事件．‎ 故选：A ‎　‎ ‎2．如图是2016年某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的中位数和众数依次为（　　）‎ A．84，84 B．84，85 C．86，84 D．84，86‎ ‎【考点】茎叶图．‎ ‎【分析】根据所给的茎叶图，看出七个数据，根据分数处理方法，去掉一个最高分93和一个最低分79后，把剩下的五个数字求出平均数和众数 ‎【解答】解：由茎叶图知，去掉一个最高分93和一个最低分79后，‎ 所剩数据84，84，86，84，87的中位数为84；‎ 众数为：84；‎ 故选A．‎ ‎　‎ ‎3．将一颗骰子连续抛掷两次，至少出现一次6点向上的概率是（　　）‎ A． B． C． D．‎ ‎【考点】等可能事件的概率；互斥事件的概率加法公式．‎ ‎【分析】根据题意，记至少出现一次6点向上为事件A，分析可得A的对立事件为两次都不是6点向上，分别计算将一颗骰子连续抛掷两次与两次都不是6点向上的情况数目，计算可得P（），由对立事件的概率性质可得答案．‎ ‎【解答】解：记至少出现一次6点向上为事件A，则A的对立事件为两次都不是6点向上，‎ 将一颗骰子连续抛掷两次，共有6×6=36种情况，‎ 其中两次都不是6点向上的情况有5×5=25种，‎ 可得P（）=，‎ 则P（A）=1﹣=，‎ 故选B．‎ ‎　‎ ‎4．某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=（　　）‎ A．9 B．10 C．12 D．13‎ ‎【考点】分层抽样方法．‎ ‎【分析】甲、乙、丙三个车间生产的产品数量的比依次为6：4：3，求出丙车间生产产品所占的比例，从而求出n的值．‎ ‎【解答】解：∵甲、乙、丙三个车间生产的产品件数分别是120，80，60，‎ ‎∴甲、乙、丙三个车间生产的产品数量的比依次为6：4：3，‎ 丙车间生产产品所占的比例，‎ 因为样本中丙车间生产产品有3件，占总产品的，‎ 所以样本容量n=3÷=13．‎ 故选D．‎ ‎　‎ ‎5．运行如图算法语句时，执行循环体的次数是（　　）‎ A．25 B．4 C．2 D．5‎ ‎【考点】程序框图．‎ ‎【分析】根据框图的流程依次计算程序运行的结果，直到不满足条件i＜10，确定循环的次数．‎ ‎【解答】解：由框图的流程得：第一次循环i=4；‎ 第二次循环i=5×5=25；‎ 不满足条件i＜10，退出循环，输出i=25．‎ 程序循环的次数为2．‎ 故选：C．‎ ‎　‎ ‎6．设变量x，y满足约束条件：，则z= 的（　　）‎ A．最大值为﹣ B．最小值为﹣ C．最大值为1 D．最小值为1‎ ‎【考点】简单线性规划．‎ ‎【分析】作出不等式组对应的平面区域，利用z的几何意义结合直线的斜率公式进行求解即可．‎ ‎【解答】解：作出不等式组，对应的平面区域，‎ 那么则z=的几何意义是区域内的点到定点D（﹣2，﹣2）的斜率，‎ 由图象知z与直线x=y重合时，直线的斜率最小，‎ ‎∴z的最小值为z=1，‎ 故选：D．‎ ‎　‎ ‎7．点（3，1）和点（﹣4，6）在直线3x﹣2y+a=0两侧，则a的范围是（　　）‎ A．a＜﹣7或a＞24 B．﹣7＜a＜24 C．a=﹣7或a=24 D．﹣24＜a＜7‎ ‎【考点】二元一次不等式（组）与平面区域．‎ ‎【分析】由已知点（3，1）和点（﹣4，6）分布在直线3x﹣2y+a=0的两侧，我们将A，B两点坐标代入直线方程所得符号相反，则我们可以构造一个关于a的不等式，解不等式即可得到答案．‎ ‎【解答】解：若（3，1）和点（﹣4，6）分布在直线3x﹣2y+a=0的两侧 则[3×3﹣2×1+a]×[3×（﹣4）﹣2×6+a]＜0‎ 即（a+7）（a﹣24）＜0‎ 解得﹣7＜a＜24．‎ 故选B．‎ ‎　‎ ‎8．执行如图的程序框图，若输入a，b，k分别为1，2，3，则输出的M=（　　）‎ A． B． C． D．‎ ‎【考点】程序框图．‎ ‎【分析】模拟执行程序，依次写出每次循环得到的a，b，k的值，当M=时满足条件n≤k，退出循环，输出M的值．‎ ‎【解答】解：n=1时，M=1+=，‎ n=2时，M=2+=，‎ n=3时，M=+=，‎ 故选：D．‎ ‎　‎ ‎9．执行如图所示的程序框图，如果输入的x，y∈R，那么输出的S的最大值为（　　）‎ A．0 B．1 C．2 D．3‎ ‎【考点】程序框图．‎ ‎【分析】算法的功能是求可行域内，目标还是S=3x+y的最大值，画出可行域，求得取得最大值的点的坐标，求出最大值．‎ ‎【解答】解：由程序框图知：算法的功能是求可行域内，目标还是S=3x+y的最大值，‎ 画出可行域如图：‎ 当时，S=3x+y的值最大，且最大值为3．‎ 故选：D．‎ ‎　‎ ‎10．满足条件的区域中共有整点的个数为（　　）‎ A．1 B．2 C．3 D．7‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，注意边界，可知取x=1时，y=1符合条件，从而求得可行域内的整点．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 联立，解得B（1，2），‎ 当x=1时，y=1．‎ ‎∴可行域内的整点为（1，1），共1个．‎ 故选：A．‎ ‎　‎ ‎11．在用二分法求方程log2x=x的一个近似解时，现在已经将一根锁定在（1，2）内，则下一步可断定该根所在的区间为（　　）‎ A．（1.4，2） B．（1，1.4） C．（1，1.5） D．（1.5，2）‎ ‎【考点】二分法求方程的近似解．‎ ‎【分析】根据函数的零点定理即可求出．‎ ‎【解答】解：令f（x）=log2x﹣x，‎ 则f（1）=﹣＜0，f（2）=1﹣=＞0，f（）=log2＞0，‎ 由f（1）f（1.5）＜0知根所在区间为（1，1.5）．‎ 故选：C ‎　‎ ‎12．在某地区某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居众显示可以过正常生活，有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”，根据连续7天的新增病例数计算，下列①～⑤各个选项中，一定符合上述指标的是（　　）‎ ‎①平均数； ‎ ‎②标准差S≤2； ‎ ‎③平均数且标准差S≤2；‎ ‎④平均数且极差小于或等于2；‎ ‎⑤众数等于1且极差小于或等于4．‎ A．①② B．③④ C．③④⑤ D．④⑤‎ ‎【考点】众数、中位数、平均数．‎ ‎【分析】通过举反例说明命题不符合题意，或通过根据平均数和标准差的统计意义，找出符合要求的选项即可．‎ ‎【解答】解：①错．举反倒：0，0，0，0，2，6，6；其平均数=2≤3，不符合题意；‎ ‎②错．举反倒：6，6，6，6，6，6，6；其标准差S=0≤2，不符合题意；‎ ‎③错．举反倒：0，3，3，3，3，3，6；其平均数≤3且标准差S=≤2，不符合题意；‎ ‎④对．若极差小于2，符合题意；‎ 若极差小于或等于2，有可能（1）0，1，2；（2）1，2，3；（3）2，3，4；（4）3，4，5；（5）4，5，6．‎ 在平均数≤3的条件下，只有（1）（2）（3）成立，符合题意；‎ ‎⑤对．在众数等于1且极差小于或等于4时，其最大数不超过5，符合题意．‎ 故选：D．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，满分20分，把正确的答案写在答题纸上指定位置）‎ ‎13．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据（如表），由最小二乘法求得回归方=0.67x+54.9．‎ 零件数x个 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 加工时间y（min）‎ ‎62‎ ‎75‎ ‎81‎ ‎89‎ 现发现表中有一个数据模糊看不清，请你推断出该数据的值为　　．‎ ‎【考点】最小二乘法；线性回归方程．‎ ‎【分析】根据表中所给的数据，做出横标和纵标的平均数，得到样本中心点，根据由最小二乘法求得回归方程．代入样本中心点求出该数据的值，‎ ‎【解答】解：设表中有一个模糊看不清数据为m．‎ 由表中数据得：， =，‎ 由于由最小二乘法求得回归方程．‎ 将x=30，y=代入回归直线方程，得m=68．‎ 故答案为：68．‎ ‎　‎ ‎14．如图为一个求20个数的平均数的算法语句，在横线上应填充的语句为　S=S+x　．‎ ‎【考点】伪代码．‎ ‎【分析】根据已知中程序的功能是“求20个数的平均数”，我们结合框图易得到结论．‎ ‎【解答】解：该程序运行的结果是求20个数的平均数；‎ 所以循环体需要执行20次，累加项通项公式为：S=S+x，‎ 故答案为：S=S+x．‎ ‎　‎ ‎15．总体由20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为　01　．‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ ‎【考点】简单随机抽样．‎ ‎【分析】由随机数表第1行的第5列和第6列数字开始由左到右依次取数，大于20的数字去掉，则可得第五个数字．‎ ‎【解答】解：由随机数表第1行的第5列和第6列数字开始由左到右依次取数，65＞20，72＞20，第一个数为08；‎ 第二个数为02；‎ ‎63＞20，第三个数为14；‎ 第四个数为07；‎ 第五个数为01．‎ 故答案为：01．‎ ‎　‎ ‎16．线性约束条件表示平面区域D，若在区域D上有无穷多个点（x，y），可使目标函数z=x+my取得最大值，则m=　1或﹣1　．‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作差可行域，化目标函数为直线方程的斜截式，然后分m＞0和m＜0分类求解得答案．‎ ‎【解答】解：由约束条件作出平面区域D：‎ 化目标函数z=x+my为，‎ 当m＞0时，要使目标函数z=x+my取得最大值的点（x，y）有无穷多个，则，得m=1；‎ 当m＜0时，要使目标函数z=x+my取得最大值的点（x，y）有无穷多个，则，得m=﹣1．‎ 故答案为：1或﹣1．‎ ‎　‎ 三、解答题（本大题共6小题，满分70分，把正确的答案写在答题纸上指定位置）‎ ‎17．甲、乙两台机床同时加工直径为100 mm的零件，为了检验产品的质量，从产品中各随机抽取6件进行测量，测得数据如下（单位mm）：‎ 甲：99，100，98，100，100，103‎ 乙：99，100，102，99，100，100‎ ‎（1）分别计算上述两组数据的平均数和方差；‎ ‎（2）根据（1）的计算结果，说明哪一台机床加工的这种零件更符合要求．‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】（1）根据所给的两组数据，分布求出两组数据的平均数，结果两组数据的平均数相等，再利用方差公式求两组数据的方差，得到甲的方差大于乙的方差．‎ ‎（2）对于两组数据的平均数和方差进行比较，知道两组数据的平均数相等，甲的方差大于乙的方差，说明乙机床生产的零件质量比较稳定．‎ ‎【解答】解：（1）==100mm，‎ ‎==100mm，‎ S2甲= [（99﹣100）2+2+（98﹣100）2+2+2+2]= mm2．‎ S2乙= [（99﹣100）2+2+2+（99﹣100）2+2+2]=1mm2．‎ ‎（2）因为两个机床产品的平均数相等，且S2甲＞S2乙，说明甲机床加工零件波动比较大，‎ 因此乙机床加工零件更符合要求．‎ ‎　‎ ‎18．某工厂制造A种仪器45台，B种仪器55台，现需用薄钢板给每台仪器配一个外壳．已知钢板有甲、乙两种规格：甲种钢板每张面积2m2，每张可做A种仪器外壳3个和B种仪器外壳5个，乙种钢板每张面积3m2，每张可做A种仪器外壳6个和B种仪器外壳6个．问甲、乙两种钢板各用多少张才能用料最省（“用料最省”是指所用钢板的总面积最小）．‎ ‎【考点】简单线性规划的应用．‎ ‎【分析】明确题意，设用甲种钢板x张，乙种钢板y张，列出关于x，y的 不等式组以及目标函数，利用线性规划问题解答．‎ ‎【解答】解：设用甲种钢板x张，乙种钢板y张，由题意，‎ 设钢板总面积S=2x+3y，适合不等式组的点（x，y）的集合 如右图阴影所示，‎ 直线l1：3x+6y=45与直线l2：5x+6y=55的交点P（5，5），‎ 当直线l：2x+3y=S经过P点时S最小．‎ ‎∴甲种钢板、乙种钢板各用5张时用料最省．‎ ‎　‎ ‎19．某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的所有数据．‎ B地区用户满意度评分：92，60，69，70，76，82，70，85，72，87，67，50，91，96，70，82，94，85，75，59，74，89，77，88，78，67，79，94，78，65，64，73，60，75，86，65，90，84，74，80‎ ‎（1）完成B地区用户满意度评分的频率分布表并作出频率分布直方图；‎ B地区用户满意度评分的频率分布表 满意度评分分组 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ ‎[90，100）‎ 频数 频率 ‎（2）通过直方图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；‎ ‎（3）根据用户满意度评分，将用户的满意度分为三个等级：‎ 满意度评分 低于70分 ‎70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 利用样本近似估计总体的思想方法，估计哪个地区用户的满意度等级为不满意的概率大？说明理由．‎ ‎【考点】频率分布直方图．‎ ‎【分析】（1）根据题意填写B地区用户满意度评分的频率分布表，画出频率分布直方图即可；‎ ‎（2）通过两地区用户满意度评分的频率分布直方图，分析结论即可；‎ ‎（3）计算A、B地区用户的满意度等级为不满意的频率值，用频率估计概率即可．‎ ‎【解答】解：（1）B地区用户满意度评分的频率分布表如下；‎ 满意度评分分组 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ ‎[90，100）‎ 频数 ‎2‎ ‎8‎ ‎14‎ ‎10‎ ‎6‎ 频率 ‎0.05‎ ‎0.2‎ ‎0.35‎ ‎0.25‎ ‎0.15‎ B地区用户满意度评分的频率分布直方图如下；‎ ‎（2）通过两地区用户满意度评分的频率分布直方图可以看出，‎ B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值，‎ B地区用户满意度评分比较集中，而A地区用户满意度评分比较分散；‎ ‎（3）记A表示事件：“A地区用户的满意度等级为不满意”，‎ B表示事件：“B地区用户的满意度等级为不满意”；‎ 由直方图得P（A）的估计值为（0.01+0.02+0.03）×10=0.6，‎ P（B）的估计值为（0.005+0.02）×10=0.25；‎ 所以A地区用户的满意度等级为不满意的概率大．‎ ‎　‎ ‎20．设关于x的一元二次方程x2+2ax+b2=0．‎ ‎（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．‎ ‎（2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．‎ ‎【考点】古典概型及其概率计算公式；几何概型．‎ ‎【分析】首先分析一元二次方程有实根的条件，得到a≥b ‎（1）本题是一个古典概型，试验发生包含的基本事件可以通过列举得到结果数，满足条件的事件在前面列举的基础上得到结果数，求得概率．‎ ‎（2）本题是一个几何概型，试验的全部结束所构成的区域为{（a，b）|0≤a≤3，0≤b≤2}，满足条件的构成事件A的区域为{（a，b）|0≤a≤3，0≤b≤2，a≥b}，根据概率等于面积之比，得到概率．‎ ‎【解答】解：设事件A为“方程有实根”．‎ 当a＞0，b＞0时，方程有实根的充要条件为a≥b ‎（1）由题意知本题是一个古典概型，试验发生包含的基本事件共12个：‎ ‎（0，0）（0，1）（0，2）（1，0）（1，1）（1，2）（2，0）（2，1）（2，2）（3，0）（3，1）（3，2）‎ 其中第一个数表示a的取值，第二个数表示b的取值．‎ 事件A中包含9个基本事件，‎ ‎∴事件A发生的概率为P==‎ ‎（2）由题意知本题是一个几何概型，‎ 试验的全部结束所构成的区域为{（a，b）|0≤a≤3，0≤b≤2}‎ 满足条件的构成事件A的区域为{（a，b）|0≤a≤3，0≤b≤2，a≥b}‎ ‎∴所求的概率是 ‎　‎ ‎21．某车间为了制定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的 零件的个数x（个）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 加工的时间y（小时）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ 数据如下：‎ ‎（1）在给定的坐标系中画出表中数据的散点图；‎ ‎（2）求出y关于x的线性回归方程=x+，并在坐标系中画出回归直线；‎ ‎（3）试预测加工10个零件需要多少小时？‎ ‎（注： =， =﹣）‎ ‎【考点】线性回归方程．‎ ‎【分析】（1）根据表中所给的数据，可得散点图；‎ ‎（2）求出出横标和纵标的平均数，得到样本中心点，求出对应的横标和纵标的积的和，求出横标的平方和，做出系数和a的值，写出线性回归方程．‎ ‎（3）将x=10代入回归直线方程，可得结论．‎ ‎【解答】解：（1）作出散点图如下：‎ ‎…‎ ‎（2）=3.5， =3.5，…∧‎ ‎=54， xiyi=52.5‎ ‎∴==0.7‎ ‎=3.5﹣0.7×3.5=1.05，‎ ‎∴所求线性回归方程为： =0.7x+1.05…‎ ‎（3）当x=10代入回归直线方程，得=0.7×10+1.05=8.05（小时）．‎ 所以加工10个零件大约需要8.05个小时…‎ ‎　‎ ‎22．某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：‎ X ‎1‎ ‎2‎ ‎3‎ ‎4‎ Y ‎51‎ ‎48‎ ‎45‎ ‎42‎ 这里，两株作物“相近”是指它们之间的直线距离不超过1米．‎ ‎（1）完成下表，并求所种作物的平均年收获量：‎ Y ‎51‎ ‎48‎ ‎45‎ ‎42‎ 频数 ‎（2）在所种年收获量为51或48的作物中随机选取两株求收获量之和，收获量之和为t的概率．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】（1）所种作物的总株数为15，其中“相近”作物株数为1的作物有2株，“相近”作物株数为2的作物有4株，“相近”作物株数为3的作物有6株，“相近”作物株数为4的作物有3株，由此能求出所种作物的平均年收获量．‎ ‎（2）记年收获量是51的两株作物为1，2；年收获量是48的四株作物为A，B，C，D，共有15个基本事件．由此能求出结果．‎ ‎【解答】解：（1）所种作物的总株数为1+2+3+4+5=15，‎ 其中“相近”作物株数为1的作物有2株，“相近”作物株数为2的作物有4株，‎ ‎“相近”作物株数为3的作物有6株，“相近”作物株数为4的作物有3株，‎ 列表如下：‎ Y ‎51‎ ‎48‎ ‎45‎ ‎42‎ 频数 ‎2‎ ‎4‎ ‎6‎ ‎3‎ 所种作物的平均年收获量为 ‎===46．‎ ‎（2）记年收获量是51的两株作物为1，2；‎ 年收获量是48的四株作物为A，B，C，D，共有15个基本事件．‎ 当t=96时，P（t=96）=；当t=99时，P（t=99）=；‎ 当t=102时，P（t=102）=．‎ ‎　‎ ‎2017年1月5日