2018年广东省佛山市高考数学一模试卷（文科）

2018年广东省佛山市高考数学一模试卷（文科）

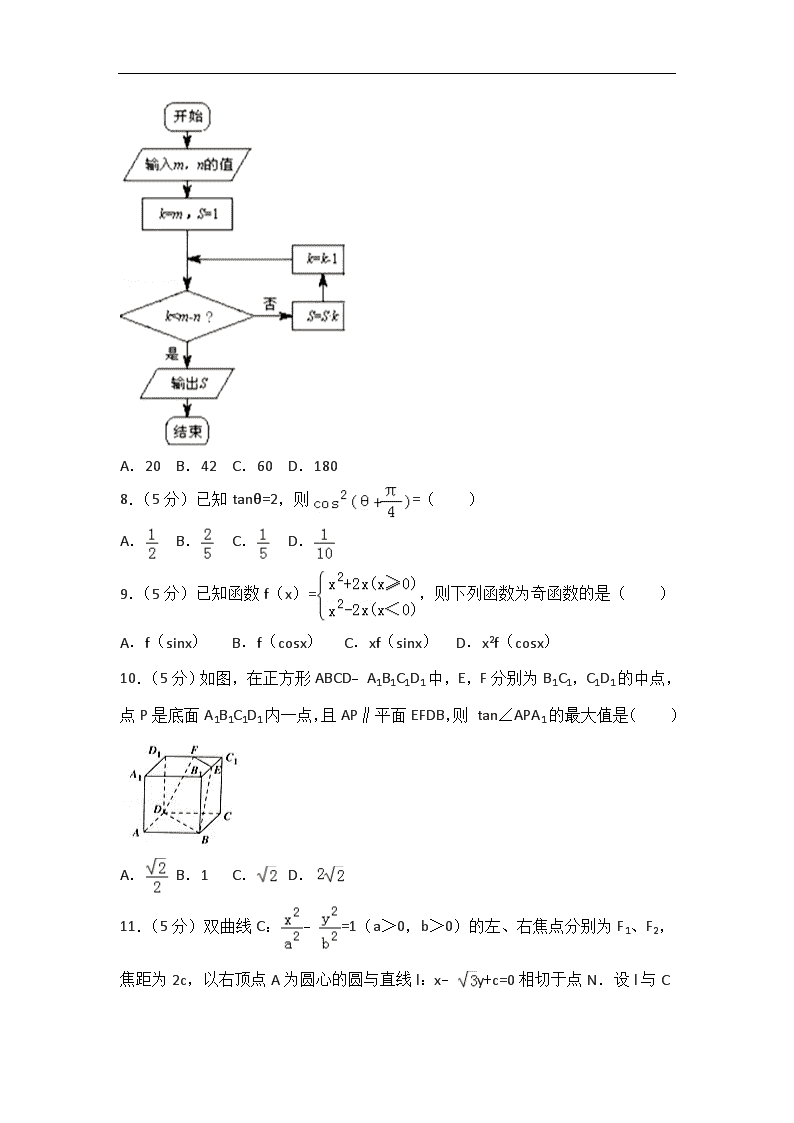
‎2018年广东省佛山市高考数学一模试卷（文科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）已知集合A={﹣1，0，1}，B={x|x﹣x2=0}，则A∩B=（　　）‎ A．{0} B．{1} C．（0，1） D．{0，1}‎ ‎2．（5分）设复数z1=2+i，z2=1+ai，若，则实数a=（　　）‎ A．﹣2 B． C． D．2‎ ‎3．（5分）若变量x，y满足约束条件，则z=3x﹣2y的最小值为（　　）‎ A．﹣1 B．0 C．3 D．9‎ ‎4．（5分）袋中有5个球，其中红色球3个，标号分别为1，2，3；篮色球2个，标号分别为1，2；从袋中任取两个球，则这两个球颜色不同且标号之和不小于4的概率为（　　）‎ A． B． C． D．‎ ‎5．（5分）已知命题p：∀x＞1，log2x+4logx2＞4，则¬p为（　　）‎ A．¬p：∀x≤1，log2x+4logx2≤4 B．¬p：∃x≤1，log2x+4logx2≤4‎ C．¬p：∃x＞1，log2x+4logx2=4 D．¬p：∃x＞1，log2x+4logx2≤4‎ ‎6．（5分）把曲线上所有点向右平移个单位长度，再把得到的曲线上所有点的横坐标缩短为原来的，得到曲线C2，则C2（　　）‎ A．关于直线对称 B．关于直线对称 C．关于点对称 D．关于点（π，0）对称 ‎7．（5分）当m=5，n=2时，执行如图所示的程序框图，输出的S值为（　　）‎ A．20 B．42 C．60 D．180‎ ‎8．（5分）已知tanθ=2，则=（　　）‎ A． B． C． D．‎ ‎9．（5分）已知函数f（x）=，则下列函数为奇函数的是（　　）‎ A．f（sinx） B．f（cosx） C．xf（sinx） D．x2f（cosx）‎ ‎10．（5分）如图，在正方形ABCD﹣A1B1C1D1中，E，F分别为B1C1，C1D1的中点，点P是底面A1B1C1D1内一点，且AP∥平面EFDB，则 tan∠APA1的最大值是（　　）‎ A． B．1 C． D．‎ ‎11．（5分）双曲线C：﹣=1（a＞0，b＞0）的左、右焦点分别为F1、F2，焦距为2c，以右顶点A为圆心的圆与直线l：x﹣y+‎ c=0相切于点N．设l与C的交点为P、Q，若点N恰为线段PQ的中点，则双曲线C的离心率为（　　）‎ A． B． C．2 D．2‎ ‎12．（5分）设函数f（x）=x3﹣3x2+2x，若x1，x2（x1＜x2）是函数g（x）=f（x）﹣λx的两个极值点，现给出如下结论：‎ ‎①若﹣1＜λ＜0，则f（x1）＜f（x2）；‎ ‎②若0＜λ＜2，则f（x1）＜f（x2）；‎ ‎③若λ＞2，则f（x1）＜f（x2）．‎ 其中正确结论的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）设=（1，2），=（﹣1，1），=+λ，若⊥，则实数λ的值等于　 　．‎ ‎14．（5分）设曲线y=xlnx在点（1，0）处的切线与曲线在点P处的切线垂直，则点P的横坐标为　 　．‎ ‎15．（5分）△ABC内角A，B，C的对边分别为a，b，c，若，则△ABC的面积S=　 　．‎ ‎16．（5分）平面四边形ABCD中，，沿直线AC将△ACD翻折成△ACD'，当三棱锥D'﹣ABC的体积取得最大值时，该三棱锥的外接球的表面积是　 　．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）已知数列{an}是等比数列，数列{bn}满足．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求数列{bn}的前n项和Sn．‎ ‎18．（12分）某课外实习作业小组调查了1000名职场人士，就入职廊架公司的意愿做了统计，得到如下数据分布：‎ ‎ 人员结构 选择意愿 ‎ 40岁以上（含40岁）男性 ‎ 40岁以上（含40岁）女性 ‎ 40岁以下男性 ‎ 40岁以下女性 ‎ 选择甲公司 ‎ 110‎ ‎ 120‎ ‎ 140‎ ‎ 80‎ ‎ 选择乙公司 ‎ 150‎ ‎ 90‎ ‎ 200‎ ‎ 110‎ ‎（1）请分布计算40岁以上（含40岁）与40岁以下全体中选择甲公司的概率（保留两位小数），根据计算结果，你能初步得出什么结论？‎ ‎（2）若分析选择意愿与年龄这两个分类变量，计算得到的K2的观测值为k1=5.5513，测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少？并用统计学知识分析，选择意愿与年龄变量和性别变量哪一个关联性更大？‎ 附：‎ P（K2≥k）‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ k ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎19．（12分）如图，已知四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，AB=AD=2，CD=4，PC=PD，∠PAB=∠PAD=60°．‎ ‎（1）证明：顶点P在底面ABCD的射影为边CD的中点；‎ ‎（2）点Q在PB上，且DQ⊥PB，求三棱锥Q﹣BCD的体积．‎ ‎20．（12分）已知椭圆的右顶点与抛物线的焦点重合，椭圆C1的离心率为，过椭圆C1‎ 的右焦点F且垂直于x轴的直线截抛物线所得的弦长为4．‎ ‎（1）求椭圆C1和抛物线C2的方程；‎ ‎（2）过点A（﹣2，0）的直线l与C2交于M，N两点，点M关于x轴的对称点为M'，证明：直线M'N恒过一定点．‎ ‎21．（12分）已知函数，（其中a∈R）‎ ‎（1）若a＞0，讨论函数f（x）的单调性；‎ ‎（2）若a＜0，求证：函数f（x）有唯一的零点．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22．（10分）在直角坐标系xOy中，直线l的参数方程为为参数，0≤α＜π），曲线C的参数方程为为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．‎ ‎（1）求曲线C的极坐标方程；‎ ‎（2）设C与l交于M，N两点（异于原点），求|OM|+|ON|的最大值．‎ ‎23．已知函数f（x）=x|x﹣a|，a∈R．‎ ‎（1）若f（1）+f（﹣1）＞1，求a的取值范围；‎ ‎（2）若a＞0，对∀x，y∈（﹣∞，a]，都有不等式恒成立，求a的取值范围．‎ ‎　‎ ‎2018年广东省佛山市高考数学一模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）已知集合A={﹣1，0，1}，B={x|x﹣x2=0}，则A∩B=（　　）‎ A．{0} B．{1} C．（0，1） D．{0，1}‎ ‎【解答】解：B={x|x﹣x2=0}={0，1}，‎ 则A∩B={0，1}，‎ 故选：D ‎　‎ ‎2．（5分）设复数z1=2+i，z2=1+ai，若，则实数a=（　　）‎ A．﹣2 B． C． D．2‎ ‎【解答】解：∵z1=2+i，z2=1+ai，‎ ‎∴，‎ 若，则1﹣2a=0，即a=．‎ 故选：C．‎ ‎　‎ ‎3．（5分）若变量x，y满足约束条件，则z=3x﹣2y的最小值为（　　）‎ A．﹣1 B．0 C．3 D．9‎ ‎【解答】解：画出变量x，y满足约束条件可行域如图阴影区域：‎ 目标函数z=3x﹣2y可看做y=x﹣z，即斜率为，‎ 截距为﹣z的动直线，‎ 数形结合可知，当动直线过点A时，z最小 由 得A（﹣1，﹣1）‎ ‎∴目标函数z=3x﹣2y的最小值为z=﹣3×0+2×1=﹣1．‎ 故选：A．‎ ‎　‎ ‎4．（5分）袋中有5个球，其中红色球3个，标号分别为1，2，3；篮色球2个，标号分别为1，2；从袋中任取两个球，则这两个球颜色不同且标号之和不小于4的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：袋中有5个球，其中红色球3个，标号分别为1，2，3；篮色球2个，标号分别为1，2；‎ 从袋中任取两个球，基本事件有10个，分别为：‎ ‎（红1，红2），（红1，红3），（红1，篮1），（红1，篮2），（红2，红3），‎ ‎（红2，篮1），（红2，篮2），（红3，篮1），（红3，篮2），（篮1，篮2），‎ 这两个球颜色不同且标号之和不小于4包含的基本事件有3个，分别为：‎ ‎（红2，篮2），（红3，篮1），（红3，篮2），‎ 故这两个球颜色不同且标号之和不小于4的概率为p=．‎ 故选：A．‎ ‎　‎ ‎5．（5分）已知命题p：∀x＞1，log2x+4logx2＞4，则¬p为（　　）‎ A．¬p：∀x≤1，log2x+4logx2≤4 B．¬p：∃x≤1，log2x+4logx2≤4‎ C．¬p：∃x＞1，log2x+4logx2=4 D．¬p：∃x＞1，log2x+4logx2≤4‎ ‎【解答】解：命题是全称命题，则命题的否定是特称命题，‎ 即：¬p：∃x＞1，log2x+4logx2≤4，‎ 故选：D．‎ ‎　‎ ‎6．（5分）把曲线上所有点向右平移个单位长度，再把得到的曲线上所有点的横坐标缩短为原来的，得到曲线C2，则C2（　　）‎ A．关于直线对称 B．关于直线对称 C．关于点对称 D．关于点（π，0）对称 ‎【解答】解：把曲线上所有点向右平移个单位长度，‎ 可得y=2sin（x﹣﹣）=2sin（x﹣）的图象；‎ 再把得到的曲线上所有点的横坐标缩短为原来的，得到曲线C2：y=2sin（2x﹣）的图象，‎ 对于曲线C2：y=2sin（2x﹣）：‎ 令x=，y=1，不是最值，故它的图象不关于直线对称，故A错误；‎ 令x=，y=2，为最值，故它的图象关于直线对称，故B正确；‎ 令x=，y=﹣1，故它的图象不关于点对称，故C错误；‎ 令x=π，y=﹣，故它的图象不关于点（π，0）对称，故D错误，‎ 故选：B．‎ ‎　‎ ‎7．（5分）当m=5，n=2时，执行如图所示的程序框图，输出的S值为（　　）‎ A．20 B．42 C．60 D．180‎ ‎【解答】解：由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S=5×4×3的值，‎ S=5×4×3=60．‎ 故选：C．‎ ‎　‎ ‎8．（5分）已知tanθ=2，则=（　　）‎ A． B． C． D．‎ ‎【解答】解：tanθ=2，则 ‎=‎ ‎=‎ ‎=‎ ‎=‎ ‎=‎ ‎=．‎ 故选：D．‎ ‎　‎ ‎9．（5分）已知函数f（x）=，则下列函数为奇函数的是（　　）‎ A．f（sinx） B．f（cosx） C．xf（sinx） D．x2f（cosx）‎ ‎【解答】解：根据题意，对于函数f（x）=，‎ 当x＞0时，f（x）=x2+2x，则有﹣x＜0，f（﹣x）=（﹣x）2﹣2（﹣x）=x2+2x，‎ 则函数f（x）为偶函数，‎ 分析选项：‎ 对于A，设g（x）=f（sinx），有g（﹣x）=f[sin（﹣x）]=f（﹣sinx）=f（sinx）=g（x），为偶函数，不符合题意；‎ 对于B，设g（x）=f（cosx），有g（﹣x）=f[cos（﹣x）]=f（cosx）=g（x），为偶函数，不符合题意；‎ 对于C，设g（x）=xf（sinx），有g（﹣x）=（﹣x）f[sin（﹣x）]=﹣xf（﹣sinx）=﹣xf（sinx）=﹣g（x），为奇函数，符合题意；‎ 对于D，设g（x）=x2f（sinx），有g（﹣x）=（﹣x）2f[sin（﹣x）]=x2f（﹣sinx）=x2f（sinx）=g（x），为偶函数，不符合题意；‎ 故选：C．‎ ‎　‎ ‎10．（5分）如图，在正方形ABCD﹣A1B1C1D1中，E，F分别为B1C1，C1D1的中点，点P是底面A1B1C1D1内一点，且AP∥平面EFDB，则 tan∠APA1的最大值是（　　）‎ A． B．1 C． D．‎ ‎【解答】解：连结AC、BD，交于点O，连结A1C1，交EF于M，连结OM，‎ 设正方形ABCD﹣A1B1C1D1中棱长为1，‎ ‎∵在正方形ABCD﹣A1B1C1D1中，E，F分别为B1C1，C1D1的中点，‎ 点P是底面A1B1C1D1内一点，且AP∥平面EFDB，‎ ‎∴AOPM，∴A1P=C1M=，‎ ‎∴tan∠APA1===2．‎ ‎∴tan∠APA1的最大值是2．‎ 故选：D．‎ ‎　‎ ‎11．（5分）双曲线C：﹣=1（a＞0，b＞0）的左、右焦点分别为F1、F2，焦距为2c，以右顶点A为圆心的圆与直线l：x﹣y+c=0相切于点N．设l与C的交点为P、Q，若点N恰为线段PQ的中点，则双曲线C的离心率为（　　）‎ A． B． C．2 D．2‎ ‎【解答】解：如图，∵以右顶点A为圆心的圆与直线l：x﹣y+c=0相切于点N，‎ ‎∴，‎ ‎∵直线l：x﹣y+c=0的倾斜角为300，‎ ‎，∠NAF1=600，‎ ‎∴‎ 由，得（y2﹣2．‎ yN=‎ 整理得：c3﹣3c2a+4a3=0⇒e3﹣3e2+4=0，‎ ‎（e3+1）﹣3（e2﹣1）=0⇒（e+1）（e2﹣4e+4）=0．‎ ‎∴e=2，‎ 故选：C ‎　‎ ‎12．（5分）设函数f（x）=x3﹣3x2+2x，若x1，x2（x1＜x2）是函数g（x）=f（x）﹣λx的两个极值点，现给出如下结论：‎ ‎①若﹣1＜λ＜0，则f（x1）＜f（x2）；‎ ‎②若0＜λ＜2，则f（x1）＜f（x2）；‎ ‎③若λ＞2，则f（x1）＜f（x2）．‎ 其中正确结论的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：函数g（x）=f（x）﹣λx，‎ ‎∴g′（x）=f′（x）﹣λ，‎ 令g′（x）=0，‎ ‎∴f′（x）﹣λ=0，‎ 即f′（x）=λ有两解x1，x2，（x1＜x2）‎ ‎∵f（x）=x3﹣3x2+2x，‎ ‎∴f′（x）=3x2﹣6x+2，‎ 分别画出y=f′（x）与y=λ的图象如图所示：‎ ‎①当﹣1＜λ＜0时，则f（x1）＞f（x2）；‎ ‎②若0＜λ＜2，则f（x1）＞f（x2）；‎ ‎③若λ＞2，则f（x1）＜f（x2）．‎ 故选：B．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）设=（1，2），=（﹣1，1），=+λ，若⊥，则实数λ的值等于　﹣5　．‎ ‎【解答】解：=+λ=（1，2）+λ（﹣1，1）=（1﹣λ，2+λ），‎ ‎∵⊥，∴=1﹣λ+2（2+λ）=0，‎ 则实数λ=﹣5‎ 故答案为：﹣5．‎ ‎　‎ ‎14．（5分）设曲线y=xlnx在点（1，0）处的切线与曲线在点P处的切线垂直，则点P的横坐标为　±2　．‎ ‎【解答】解：由y=xlnx，得y′=1+lnx，‎ ‎∴y′|x=1=1，‎ 由y=，得y′=﹣，设P（x0，y0），‎ 则y′=|=﹣，‎ 由题意可得：﹣=﹣1，‎ ‎∴x0=±2．‎ 则P点的横坐标为±2．‎ 故答案为：±2．‎ ‎　‎ ‎15．（5分）△ABC内角A，B，C的对边分别为a，b，c，若，则△ABC的面积S=　　．‎ ‎【解答】解：△ABC中，∵cosA=，可得：sinA==，‎ ‎∴由正弦定理可得：b===7，‎ ‎∴由余弦定理b2=a2+c2﹣2accosB，可得：49=25+c2﹣5c，解得：c=8或﹣3（舍去），‎ ‎∴S△ABC=acsinB==．‎ 故答案为：．‎ ‎　‎ ‎16．（5分）平面四边形ABCD中，，沿直线AC将△ACD翻折成△ACD'，当三棱锥D'﹣ABC的体积取得最大值时，该三棱锥的外接球的表面积是　24π　．‎ ‎【解答】解：在三角形ABC中，由余弦定理可得cosB==﹣，‎ 则sinB==，=2，则AC边上的高为h=1，平面四边形ABCD中，，四边形是筝形，AC⊥BD，当三棱锥D'﹣ABC的体积取得最大值时，△ACD翻折成△ACD'两个三角形所在平面垂直，‎ 建立如图所示的空间直角坐标系，如图：则A（0，0，0），B（0，1，1），C（0，4，0），D（1，1，0），设外接球的球心为（x，y，z），则|OA|=|OB|=|OC|=|OD|，‎ 可得：，‎ 解得x=﹣1；y=2，z=﹣1，外接球的半径为：r=|OA|==，‎ 外接球的表面积为：4πr2=24π；‎ 故答案为：24π．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）已知数列{an}是等比数列，数列{bn}满足．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求数列{bn}的前n项和Sn．‎ ‎【解答】解：（1）因为an+1+bn=n，则a2+b1=1，得a2=4，a3+b2=2，得a3=8，‎ 因为数列{an}是等比数列，所以，‎ 所以．‎ ‎（2）由（1）可得，‎ 所以 ‎=．‎ ‎　‎ ‎18．（12分）某课外实习作业小组调查了1000名职场人士，就入职廊架公司的意愿做了统计，得到如下数据分布：‎ ‎ 人员结构 ‎ 40岁以下男 ‎ 40岁以下女 选择意愿 ‎ 40岁以上（含40岁）男性 ‎ 40岁以上（含40岁）女性 性 性 ‎ 选择甲公司 ‎ 110‎ ‎ 120‎ ‎ 140‎ ‎ 80‎ ‎ 选择乙公司 ‎ 150‎ ‎ 90‎ ‎ 200‎ ‎ 110‎ ‎（1）请分布计算40岁以上（含40岁）与40岁以下全体中选择甲公司的概率（保留两位小数），根据计算结果，你能初步得出什么结论？‎ ‎（2）若分析选择意愿与年龄这两个分类变量，计算得到的K2的观测值为k1=5.5513，测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少？并用统计学知识分析，选择意愿与年龄变量和性别变量哪一个关联性更大？‎ 附：‎ P（K2≥k）‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ k ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎【解答】解：（1）设40岁以上（含40岁）与40岁以下群体中选择甲公司的概率分别为P1，P2，‎ 由数据知P1==≈0.49，‎ P2==≈0.42，‎ 因为P1＞P2，‎ 所以年龄40岁以上（含40岁）的群体选择甲公式的可能性要大；‎ ‎（2）因为k1=0.5513＞5.024，根据表中对应值，‎ 得出“选择意愿与年龄有关系”的结论犯错的概率的上限是0.025，‎ 由数据分布可得选择意愿与性别两个分类变量的2×2列联表：‎ 选择甲公司 选择乙公司 合计 男 ‎250‎ ‎350‎ ‎600‎ 女 ‎200‎ ‎200‎ ‎400‎ 合计 ‎450‎ ‎550‎ ‎1000‎ 计算K2==≈6.734，‎ 且K2=6.734＞6.635，‎ 根据临界值表得出结论“选择意愿与性别有关”的犯错误的概率上限为0.01，‎ 由0.01＜0.025，所以与年龄相比，选择意愿与性别关联性更大．‎ ‎　‎ ‎19．（12分）如图，已知四棱锥P﹣ABCD中，AB∥CD，AB⊥AD，AB=AD=2，CD=4，PC=PD，∠PAB=∠PAD=60°．‎ ‎（1）证明：顶点P在底面ABCD的射影为边CD的中点；‎ ‎（2）点Q在PB上，且DQ⊥PB，求三棱锥Q﹣BCD的体积．‎ ‎【解答】（1）证明：取CD的中点为O，连接OP，OB，‎ 则OD=BA=2，因为AB∥CD，AB⊥AD，AB=AD=2，‎ 所以四边形ABOD是正方形，OB⊥CD，‎ 因为PC=PD，O为CD中点，所以PO⊥CD，‎ 由OP∩OB=O，所以CD⊥平面POB，PB⊂平面POB，‎ 所以CD⊥PB，因为AB∥CD，所以AB⊥PB，‎ 则在Rt△ABP中，∠PAB=60°，AB=2，‎ 所以，‎ 在Rt△DOP中，，‎ 所以OB2+OP2=4+8=12=PB2，即OP⊥OB，又CD∩OB=O 所以PO⊥底面ABCD，即顶点P在底面ABCD的射影为边CD的中点．‎ ‎（2）解：由题设与（1）可得，‎ 因为DQ⊥PB，所以，解得，所以，‎ 又，设三棱锥Q﹣BCD的高为h，则，又，‎ 所以三棱锥Q﹣BCD的体积．‎ ‎　‎ ‎20．（12分）已知椭圆的右顶点与抛物线的焦点重合，椭圆C1的离心率为，过椭圆C1的右焦点F且垂直于x轴的直线截抛物线所得的弦长为4．‎ ‎（1）求椭圆C1和抛物线C2的方程；‎ ‎（2）过点A（﹣2，0）的直线l与C2交于M，N两点，点M关于x轴的对称点为M'，证明：直线M'N恒过一定点．‎ ‎【解答】解：（1）设椭圆C1的半焦距为c，依题意，可得，则，‎ 代入x=c，得y2=4ax，即，所以，‎ 则有，‎ 所以椭圆C1的方程为，抛物线C2的方程为y2=8x．‎ ‎（2）依题意，可知直线l的斜率不为0，可设l：x=my﹣2，‎ 联立，得y2﹣8my+16=0，‎ 设M（x1，y1），N（x1，y1），则M'（x1，﹣y1），‎ ‎△＞0，得m＜﹣1或m＞1，，‎ 所以直线M'N的斜率，‎ 可得直线M'N的方程为，‎ 即=，‎ 所以当m＜﹣1或m＞1时，直线M'N恒过定点（2，0）．‎ ‎　‎ ‎21．（12分）已知函数，（其中a∈R）‎ ‎（1）若a＞0，讨论函数f（x）的单调性；‎ ‎（2）若a＜0，求证：函数f（x）有唯一的零点．‎ ‎【解答】解：（1）f（x）的定义域为（0，+∞），，‎ 令f'（x）=0，即，‎ ‎①当x1=x2，即时，f'（x）≥0，f（x）是（0，+∞）上的增函数；‎ ‎②当x1＜x2，即时，‎ 当时，f'（x）＞0，f（x）单调递增，‎ 当时，f'（x）＜0，f（x）单调递减；‎ 当时，f'（x）＞0，f（x）单调递增；‎ ‎③当x2＜x1，即时，当时，f'（x）＞0，f（x）单调递增；‎ 当时，f'（x）＜0，f（x）单调递减；‎ 当时，f'（x）＞0，f（x）单调递增；‎ 综上所述，当时，f（x）在单调递增，在单调递减；‎ 当时，f（x）在（0，+∞）单调递增；‎ 当时，f（x）在单调递增，在在单调递减．‎ ‎（2）若a＜0，令f'（x）=0，即（2x﹣a）（1+lnx）=0，得，‎ 当时，f'（x）＜0，f（x）单调递减，当时，f'（x）＞0，f（x）单调递增，‎ 故当时，f（x）取得极小值，‎ 以下证明：在区间上，f（x）＜0，‎ 令，则，，，‎ 因为a＜0，t＞1，不等显然成立，故在区间上，f（x）＜0，‎ 又，即，故当a＜0时，函数f（x）有唯一的零点．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22．（10分）在直角坐标系xOy中，直线l的参数方程为为参数，0≤α＜π），曲线C的参数方程为为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．‎ ‎（1）求曲线C的极坐标方程；‎ ‎（2）设C与l交于M，N两点（异于原点），求|OM|+|ON|的最大值．‎ ‎【解答】解：（1）∵曲线C的参数方程为为参数），‎ ‎∴消去参数β，得曲线C的普通方程为x2+（y﹣2）2=4，‎ 化简得x2+y2=4y，则ρ2=4ρsinθ，‎ 所以曲线C的极坐标方程为ρ2=4ρsinθ．‎ ‎（2）∵直线l的参数方程为为参数，0≤α＜π），‎ ‎∴由直线l的参数方程可知，直线l必过点（0，2），也就是圆C的圆心，则，‎ 不妨设，其中，‎ 则，‎ 所以当，|OM|+|ON|取得最大值为．‎ ‎　‎ ‎23．已知函数f（x）=x|x﹣a|，a∈R．‎ ‎（1）若f（1）+f（﹣1）＞1，求a的取值范围；‎ ‎（2）若a＞0，对∀x，y∈（﹣∞，a]，都有不等式恒成立，求a的取值范围．‎ ‎【解答】解：（1）f（1）+f（﹣1）=|1﹣a|﹣|1+a|＞1，‎ 若a≤﹣1，则1﹣a+1+a＞1，得2＞1，即a≤﹣1时恒成立，‎ 若﹣1＜a＜1，则1﹣a﹣（1+a）＞1，得，即，‎ 若a≥1，则﹣（1﹣a）﹣（1+a）＞1，得﹣2＞1，即不等式无解，‎ 综上所述，a的取值范围是．‎ ‎（2）由题意知，要使得不等式恒成立，只需，‎ 当x∈（﹣∞，a]时，，‎ 因为，所以当时，‎ ‎，‎ 即，解得﹣1≤a≤5，结合a＞0，所以a的取值范围是（0，5]．‎ ‎　‎