专题2-10 函数最值（练）-2018年高考数学一轮复习讲练测（江苏版）

专题2-10 函数最值（练）-2018年高考数学一轮复习讲练测（江苏版）

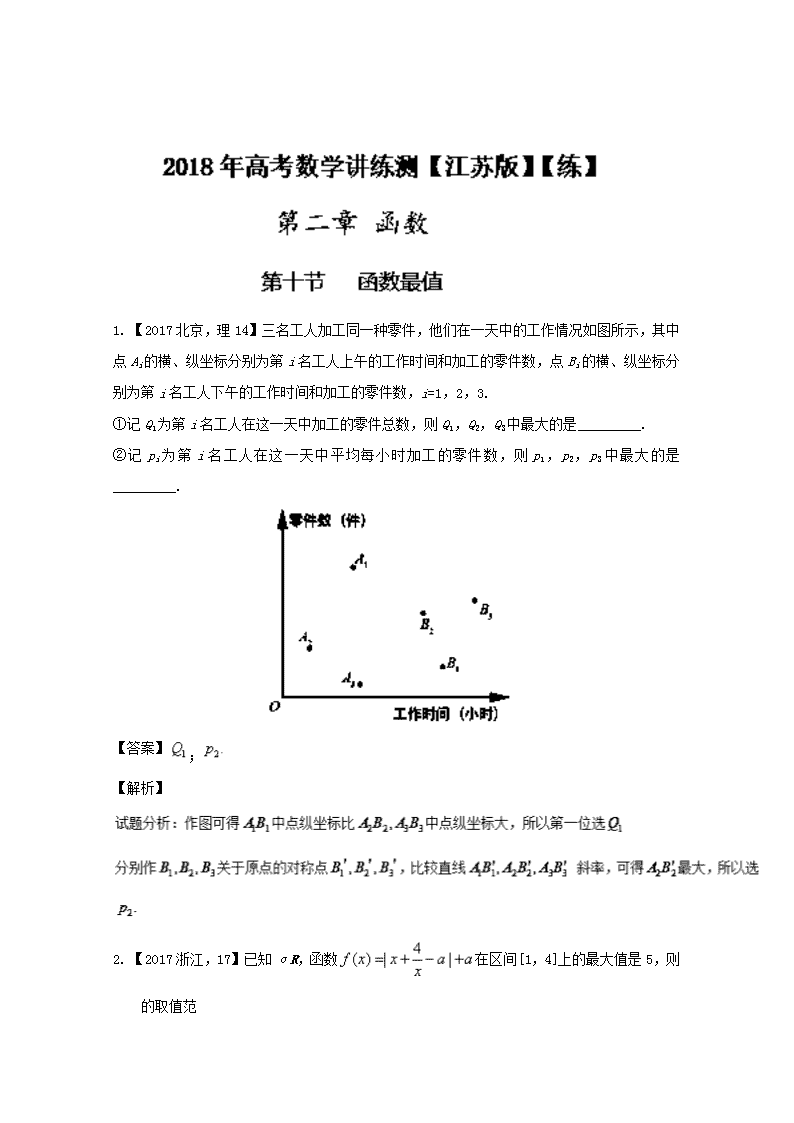
‎1. 【2017北京，理14】三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i=1，2，3.‎ ‎①记Q1为第i名工人在这一天中加工的零件总数，则Q1，Q2，Q3中最大的是_________.‎ ‎②记pi为第i名工人在这一天中平均每小时加工的零件数，则p1，p2，p3中最大的是_________.‎ ‎【答案】；‎ ‎【解析】‎ ‎2. 【2017浙江，17】已知αR，函数在区间[1，4]上的最大值是5，则的取值范 围是___________． ‎ ‎【答案】‎ ‎【解析】‎ ‎3.已知函数则的最小值为_________．‎ ‎【答案】‎ ‎【解析】当时当时,‎ 所以的值域为 ‎4.已知函数，则的最小值是 ．‎ ‎【答案】.‎ ‎5.设函数g(x)＝x2－2(x∈R)，f(x)＝，则f(x)的最小值是_________．‎ ‎【答案】‎ ‎【解析】令x0，‎ 解得x<－1或x>2.‎ 令x≥g(x)，即x2－x－2≤0，解得－1≤x≤2.‎ 故函数f(x)＝‎ 当x＜－1或x＞2时，函数f(x)＞f(－1)＝2；‎ 当－1≤x≤2时，函数≤f(x)≤f(－1)，‎ 即≤f(x)≤0.‎ 故函数f(x)的值域是∪(2，＋∞)．‎ ‎6.对于任意实数a,b定义min{a,b}=设函数f(x)=-x+3, g(x)=log2x,则函数h(x)=min{f(x),g(x)}的最大值是________．‎ ‎【答案】1‎ ‎【解析】依题意,h(x)=当02时,h(x) =3-x是减少的,所以h(x)=min{f(x),g(x)}在x=2时取得最大值h(2)=1.‎ ‎7.函数y＝的最小值为______．‎ ‎【答案】10‎ ‎8.已知函数y＝的最大值为7，最小值为－1，则m＋n的值为______．‎ ‎【答案】6‎ ‎【解析】函数式可变形为(y－m)x2－4x＋(y－n)＝0，x∈R，由已知得y－m≠0，所以 Δ＝(－4)2－4(y－m)·(y－n)≥0，即y2－(m＋n)y＋(mn－12)≤0，①‎ 由题意，知不等式①的解集为[－1,7]，则－1、7是方程y2－(m＋n)y＋(mn－12)＝0的两根，‎ 代入得，解得或 所以m＋n＝6.‎ ‎9.函数f(x)=x+2的最大值为________．‎ ‎【答案】2‎ ‎10.定义：区间[x1，x2](x1＜x2)的长度为x2－x1.已知函数y＝2|x|的定义域为[a，b]，值域为[1,2]，则区间[a，b]的长度的最大值与最小值的差为________．‎ ‎【答案】1‎ ‎【解析】[a，b]的长度取得最大值时[a，b]＝[－1,1]，区间[a，b]的长度取得最小值时[a，b]可取[0,1]或[－1,0]，因此区间[a，b]的长度的最大值与最小值的差为1.‎ ‎11.函数y＝(x>0)的最大值是________．‎ ‎【答案】 ‎【解析】由y＝(x>0)，得01)，则ab的值为______．‎ ‎【答案】‎