四川省汉源县第一中学2011-2012学年高二数学上学期期中考试 理 新人教A版

四川省汉源县第一中学2011-2012学年高二数学上学期期中考试 理 新人教A版

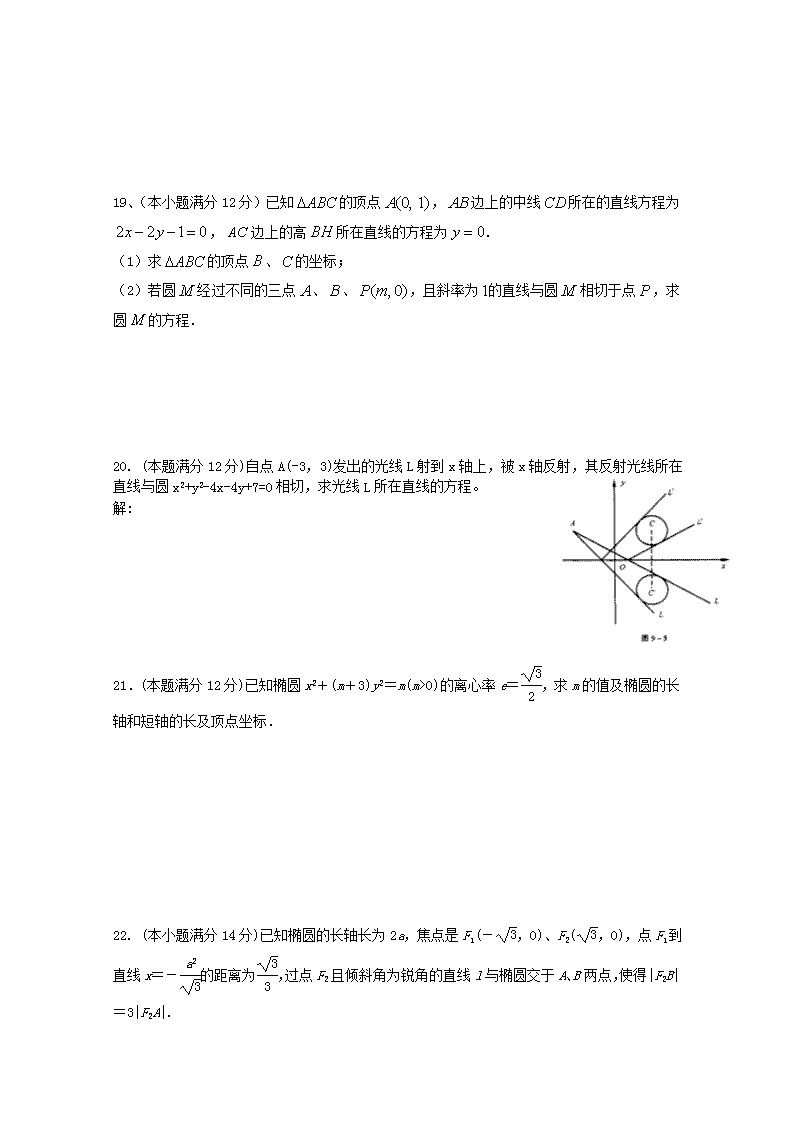
汉源一中高2013级高二上期理科数学半期试题 ‎（测试范围：直线与圆的方程、椭圆的方程）‎ 本试卷分第Ⅰ部分（选择题）和第Ⅱ部分（非选择题）共150分 考试时间120分钟. ‎ 第Ⅰ部分（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将答案填在答题卷上。‎ ‎1. 直线与直线垂直，则等于（ ）‎ A． B． C． D．‎ ‎2．圆的圆心坐标和半径分别为（ ）‎ A． B． C． D．‎ ‎3.方程y＝表示的曲线为图中的(　 　)‎ ‎4. 直线截圆得到的弦长为（ ）‎ A． B． C． D． ‎ ‎5．如右图，定圆半径为，圆心为，则直线 y O x ‎。‎ 与直线的交点在（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎6. 已知直线相切，则三条边长分别为|a|，|b|，|c|的三角形 。‎ A．是锐角三角形 B．是直角三角形 C．是钝角三角形 D．不存在 ‎7．点M(x0,y0)是圆x2+y2=a2 (a>0)内不为圆心的一点，则直线x0x+y0y=a2与该圆的位置关系是（ ）‎ A．相切 B．相交 C．相离 D．相切或相交 ‎8．设P是椭圆＋＝1上一点，F1、F2是椭圆的焦点，若|PF1|等于4，则|PF2|等于(　　)‎ A．22 B．21‎ C．20 D．13‎ ‎9．已知F1、F2是椭圆的两个焦点，满足·＝0的点M 总在椭圆内部，则椭圆离心率的取值范围是(　　)‎ A．(0,1) B. C. D. ‎10．若为圆的弦的中点，则直线的方程是（ ） ‎ A. B. ‎ C. D. ‎ ‎11．圆上的点到直线的距离最大值是（ ）‎ A． B． C． D．‎ ‎12．将直线，沿轴向左平移个单位，所得直线与圆相切，则实数的值为（　 　）‎ A． 　B． 　C．　 D．‎ 二、填空题：（共4小题，每小题5分）‎ ‎13. 点到直线的距离为_______.‎ ‎14. 圆和圆的位置关系是________.‎ ‎15.圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为______.‎ ‎16.若过椭圆＋＝1内一点(2,1)的弦被该点平分，则该弦所在直线的方程是________．‎ 三、解答题：（10+10+12+12+12+14＝70分，共6小题）‎ ‎17．（本小题满分10分）已知圆和轴相切，圆心在直线上，且被直线截得的弦长为，求圆的方程。‎ ‎18．(本小题满分12分)设椭圆的中心在原点，焦点在x轴上，离心率e＝.已知点P到这个椭圆上的点的最远距离为，求这个椭圆的方程．‎ ‎19、（本小题满分12分）已知的顶点，边上的中线所在的直线方程为，边上的高所在直线的方程为.‎ ‎（1）求的顶点、的坐标；‎ ‎（2）若圆经过不同的三点、、，且斜率为的直线与圆相切于点，求圆的方程.‎ ‎20. (本题满分12分)自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程。‎ 解:‎ ‎21．(本题满分12分)已知椭圆x2＋(m＋3)y2＝m(m>0)的离心率e＝，求m的值及椭圆的长轴和短轴的长及顶点坐标．‎ ‎22. (本小题满分14分)已知椭圆的长轴长为‎2a，焦点是F1(－，0)、F2(，0)，点F1到直线x＝－的距离为，过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点，使得|F2B|＝3|F‎2A|.‎ ‎(1)求椭圆的方程；‎ ‎(2)求直线l的方程．‎ 解：‎ 汉源一中高二上期理科数学半期试题答案 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ 题 号 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 6‎ ‎ 7‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ ‎11‎ ‎12‎ 答 案 C D C B D B C A C A B A 二、填空题：（共4小题，每小题5分）‎ ‎13. _____ __；14. __ 相交______；15. __ 2 __；16. ___ x＋2y－4＝0______.‎ 三、解答题：（10+10+12+12+12+14＝70分，共6小题）‎ ‎18、（本小题满分10分）解析：　设椭圆方程为＋＝1(a>b>0)，M(x，y)为椭圆上的点，由 eq f(c,a)＝得a＝2b.‎ ‎|PM|2＝x2＋2＝－32＋4b2＋3(－b≤y≤b)，‎ 若b<，则当y＝－b时，|PM|2最大，即2＝7，‎ 则b＝－>，故舍去．‎ 若b≥时，则当y＝－时，|PM|2最大，即4b2＋3＝7，‎ 解得b2＝1.‎ ‎∴所求方程为＋y2＝1.‎ ‎19、（本小题满分12分）已知的顶点，边上的中线所在的直线方程为，边上的高所在直线的方程为.‎ ‎（1）求的顶点、的坐标；‎ ‎（2）若圆经过不同的三点、、，且斜率为的直线与圆相切于点，求圆的方程.‎ 解：（1）边上的高所在直线的方程为，所以，，‎ 又，所以，，‎ 设，则的中点，代入方程，‎ 解得，所以. ‎ ‎（2）由，可得，圆的弦的中垂线方程为，‎ 注意到也是圆的弦，所以，圆心在直线上，‎ 设圆心坐标为，‎ 因为圆心在直线上，所以…………①，‎ 又因为斜率为的直线与圆相切于点，所以，‎ 即，整理得…………②， ‎ 由①②解得，，‎ 所以，，半径，‎ 所以所求圆方程为。‎ ‎20. (本题满分12分)自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程。‎ 解:‎ 自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程。‎ 解法一 已知圆的标准方程是(x-2)2+(y-2)2=1，它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1。设光线L所在的直线的方程是y-3=k(x+3)（其中斜率k待定），由题设知对称圆的圆心C′（2，-2）到这条直线的距离等于1，即d==1。整理得 12k2+25k+12=0，解得k= -或k= -。故所求直线方程是y-3= -(x+3)，或y-3= -(x+3)，即3x+4y-3=0或4x+3y+3=0。‎ 解法二 已知圆的标准方程是(x-2)2+(y-2)2=1，设交线L所在的直线的方程是 y-3=k(x+3)（其中斜率k待定），由题意知k≠0，于是L的反射点的坐标是（-，0），因为光线的入射角等于反射角，所以反射光线L′所在直线的方程为y= -k(x+)，即y+kx+3(1+k)=0。这条直线应与已知圆相切，故圆心到直线的距离为1，即d==1。以下同解法一。‎ ‎21．(本题满分12分) ‎ 解：椭圆方程可化为＋＝1.‎ 因为m－＝>0，所以m>.‎ 即a2＝m，b2＝，c＝＝ .‎ 由e＝，得 ＝，解得m＝1.‎ 所以a＝1，b＝，椭圆的标准方程为x2＋＝1.‎ 所以椭圆的长轴长为2，短轴长为1，‎ 四个顶点的坐标分别为 A1(－1,0)，A2(1,0)，B1(0，－)，B2(0，)．‎ ‎22. 已知椭圆的长轴长为‎2a，焦点是F1(－，0)、F2 (，0)，点F1到直线x＝－的距离为，过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点，使得|F2B|＝3|F‎2A|.‎ ‎(1)求椭圆的方程；‎ ‎(2)求直线l的方程．‎ 解析：　(1)∵F1到直线x＝－的距离为，‎ ‎∴－＋＝.‎ ‎∴a2＝4.‎ 而c＝，‎ ‎∴b2＝a2－c2＝1.‎ ‎∵椭圆的焦点在x轴上，‎ ‎∴所求椭圆的方程为＋y2＝1.‎ ‎(2)设A(x1，y1)、B(x2，y2)．‎ ‎∵|F2B|＝3|F‎2A|，‎ ‎∴ ‎∵A、B在椭圆＋y2＝1上，∴ ‎∴∴l的斜率为＝.‎ ‎∴l的方程为y＝(x－)，即x－y－＝0.‎ ‎ ‎