- 2021-06-30 发布 |
- 37.5 KB |
- 3页


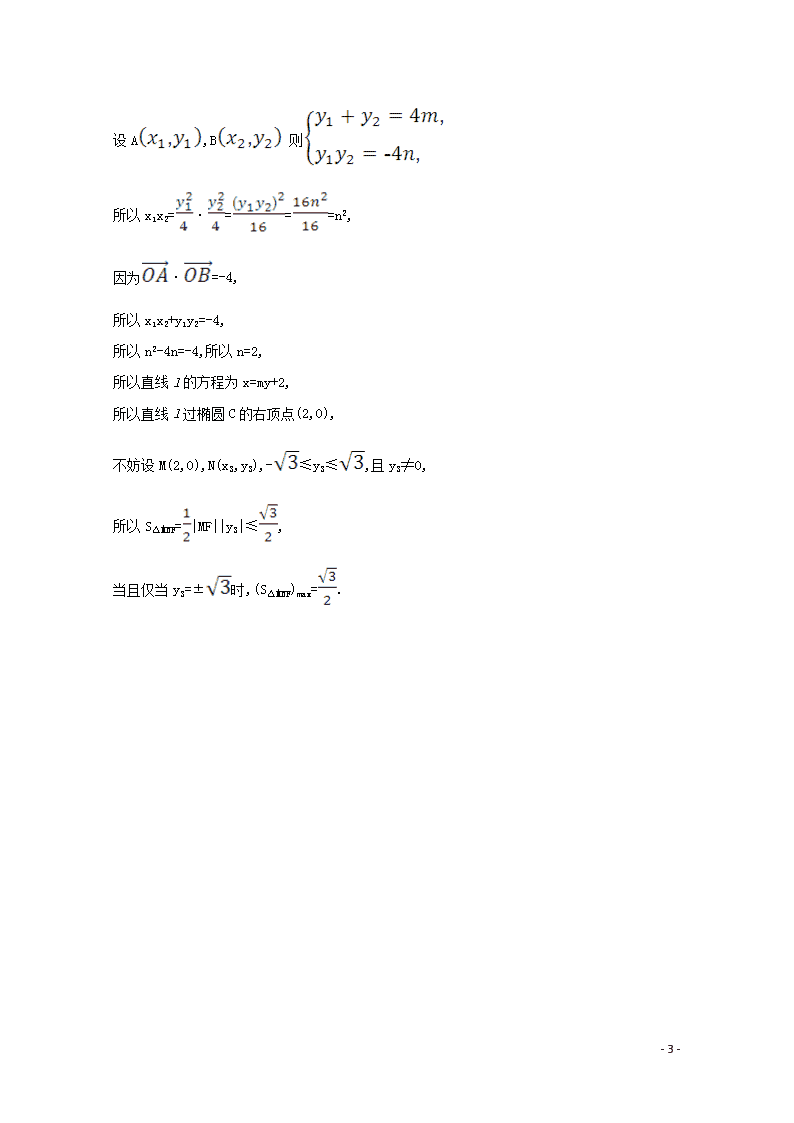
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学一轮复习核心素养测评五十九10-9-2圆锥曲线中的探究性问题文含解析北师大版
核心素养测评五十九 圆锥曲线中的探究性问题 1.(2019·德州模拟)已知椭圆C:+=1(a>b>0)的左右焦点分别为F1,F2,离心率为,P是椭圆C上的一个动点,且△PF1F2面积的最大值为. (1)求椭圆C的方程. (2)设直线PF2斜率为k(k≠0),且PF2与椭圆C的另一个交点为Q,是否存在点T(0,t),使得|TP|=|TQ|.若存在,求t的取值范围;若不存在,请说明理由. 【解析】(1)当P为C的短轴顶点时,△PF1F2的面积有最大值, 所以 ,解得 , 故椭圆C的方程为:+=1. (2)设直线PQ的方程为y=k(x-1), 将y=k(x-1)代入+=1, 得x2-8k2x+4k2-12=0; 设P,Q,线段PQ的中点为N, x0==,y0= =k=, 即N, - 3 - 因为|TPTQ|,所以直线TN为线段PQ的垂直平分线,所以TN⊥PQ,则kTN·kPQ=-1, 即·k=-1,所以t==, 当k>0时,因为4k+≥4(当且仅当k=时取等号),所以t∈,当k<0时,因为4k+≤-4(当且仅当k=-时取等号),所以t∈.综上,存在点T,使得|TPTQ|,且t的取值范围为∪. 2.已知离心率为的椭圆C:+=1(a>b>0)的右焦点与抛物线E:y2=2px(p>0)的焦点F重合,且点F到E的准线的距离为2. (1)求椭圆C的方程. (2)若直线l与C交于M,N两点,与E交于A,B两点,且·=-4(O为坐标原点),求△MNF面积的最大值. 【解析】(1)因为点F到E的准线的距离为2, 所以p=2,F(1,0), 由 解得 所以椭圆C的方程为+=1. (2)由(1)知抛物线E的方程为y2=4x. 要使直线l与抛物线E交于两点,则直线l的斜率不为0,可设l的方程为x=my+n, 由 得y2-4my-4n=0 所以Δ=(-4m)2+16n>0,得m2+n>0. - 3 - 设A,B 则 所以x1x2=·===n2, 因为·=-4, 所以x1x2+y1y2=-4, 所以n2-4n=-4,所以n=2, 所以直线l的方程为x=my+2, 所以直线l过椭圆C的右顶点(2,0), 不妨设M(2,0),N(x3,y3),-≤y3≤,且y3≠0, 所以S△MNF=|MF||y3|≤, 当且仅当y3=±时,(S△MNF)max=. - 3 -查看更多