2019届二轮复习第3讲 不等式与线性规划学案(全国通用)
第3讲 不等式与线性规划
【p17】
【p17】
年份
卷别
题号
考查内容
命题规律
2018
Ⅰ
13
简单的线性规划问题
Ⅱ
14
简单的线性规划问题
2017
Ⅰ
14
简单的线性规划问题
Ⅱ
5
简单的线性规划问题
Ⅲ
13
简单的线性规划问题
2016
Ⅰ
16
线性规划
Ⅲ
13
简单的线性规划问题
关于不等式,主要结合集合,求某个简单一元二次不等式的解集,并求所求解集与另一集合的交(并、补);
解线性规划问题,包括由约束条件求目标函数的最值;由约束条件,求满足目标函数的最值的条件(不等式中的参数),或判断某一条件是否满足约束条件域.
备 考 建 议 【p17】
1.复习简单线性规划问题时,要重视数形结合思想的运用,同时因为最优解是通过图形观察的,所以作图要精确,否则可能导致结果有误.
典 例 剖 析 【p17】
探究一 不等式性质的应用及解不等式
例1设x∈(0,+∞)时,不等式9x-m·3x+m+1>0恒成立,则m的取值范围是( )
A.2-2
1),则由已知得函数f(t)=t2-m·t+m+1的图象在t∈(1,+∞)上恒在x轴上方.则对于方程f(t)=0,有Δ<0或解得m<2+2.
探究二 基本不等式的应用
例2已知函数f(x)=若不等式f(x)+1≥0在x∈R上恒成立,则实数a的取值范围是( )
A.(-∞,0) B.[-2,2]
C.(-∞,2] D.[0,2]
【解析】选C.
例3已知函数f(x)=ln(x+),若正实数a,b满足f(2a)+f(b-1)=0,则+的最小值是__________.
【解析】3+2
因为f(x)=ln(x+),f(-x)=ln(-x+),所以f(x)+f(-x)=0, 即f(x)在R上为奇函数.又因为f(x)在其定义域上是增函数,故2a+b=1,
所以+=(2a+b)=3++≥3+2(当且仅当a=,b=-1时等号成立).
探究三 线性目标函数的最值及取值范围
例4 (1)[2017·全国卷Ⅱ]设x,y满足约束条件则z=2x+y的最小值是( )
A.-15 B.-9
C.1 D.9
【解析】选A.
作出约束条件对应的可行域,如图中阴影部分所示,当目标函数线经过可行域中的点A(-6,-3)时,目标函数取得最小值,即zmin=2×(-6)-3=-15.故选A.
(2)实数x、y满足不等式组则w=的取值范围是( )
A. B.
C. D.
【解析】选D.
点(x,y)在图中阴影部分,w=表示动点(x,y)与定点A (-1,1)连线的斜率,l1为斜率k1=kAB=-. l2与x-y=0平行,∴w∈.
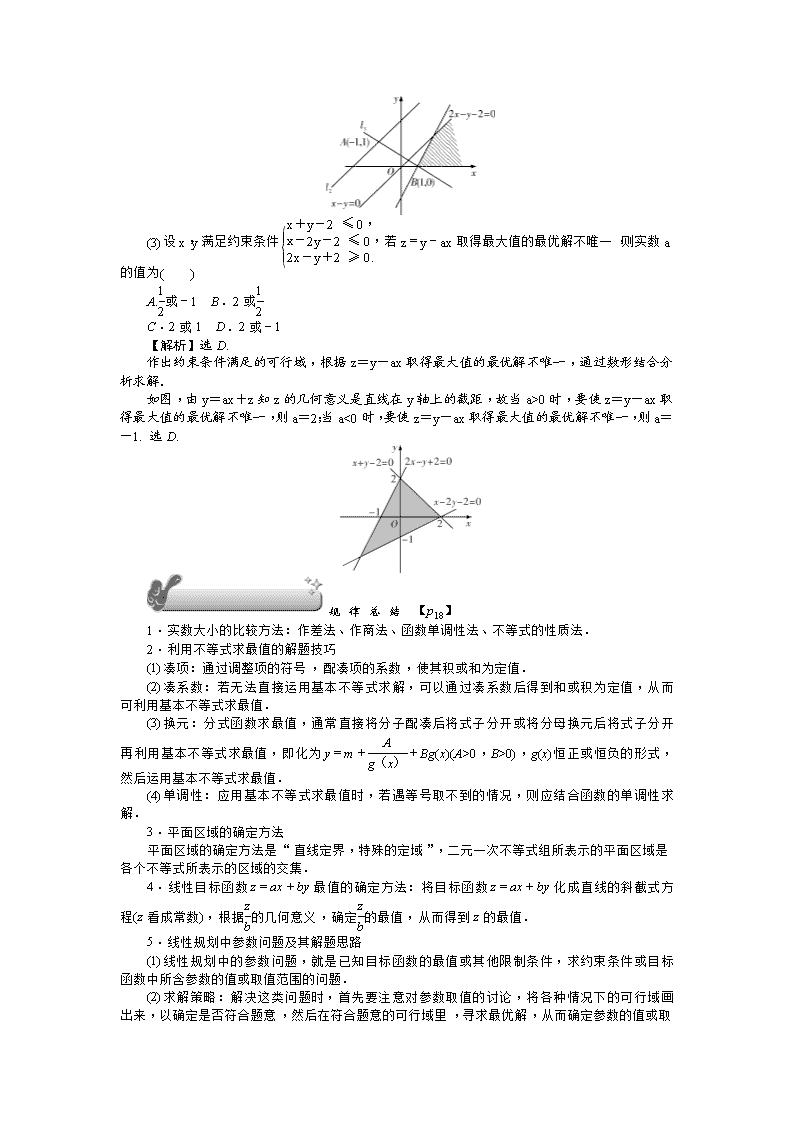
(3)设x,y满足约束条件若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )
A.或-1 B.2或
C.2或1 D.2或-1
【解析】选D.
作出约束条件满足的可行域,根据z=y-ax取得最大值的最优解不唯一,通过数形结合分析求解.
如图,由y=ax+z知z的几何意义是直线在y轴上的截距,故当a>0时,要使z=y-ax取得最大值的最优解不唯一,则a=2;当a<0时,要使z=y-ax取得最大值的最优解不唯一,则a=-1. 选D.
规 律 总 结 【p18】
1.实数大小的比较方法:作差法、作商法、函数单调性法、不等式的性质法.
2.利用不等式求最值的解题技巧
(1)凑项:通过调整项的符号,配凑项的系数,使其积或和为定值.
(2)凑系数:若无法直接运用基本不等式求解,可以通过凑系数后得到和或积为定值,从而可利用基本不等式求最值.
(3)换元:分式函数求最值,通常直接将分子配凑后将式子分开或将分母换元后将式子分开再利用基本不等式求最值,即化为y=m++Bg(x)(A>0,B>0),g(x)恒正或恒负的形式,然后运用基本不等式求最值.
(4)单调性:应用基本不等式求最值时,若遇等号取不到的情况,则应结合函数的单调性求解.
3.平面区域的确定方法
平面区域的确定方法是“直线定界,特殊的定域”,二元一次不等式组所表示的平面区域是各个不等式所表示的区域的交集.
4.线性目标函数z=ax+by最值的确定方法:将目标函数z=ax+by化成直线的斜截式方程(z看成常数),根据的几何意义,确定的最值,从而得到z的最值.
5.线性规划中参数问题及其解题思路
(1)线性规划中的参数问题,就是已知目标函数的最值或其他限制条件,求约束条件或目标函数中所含参数的值或取值范围的问题.
(2)求解策略:解决这类问题时,首先要注意对参数取值的讨论,将各种情况下的可行域画出来,以确定是否符合题意,然后在符合题意的可行域里,寻求最优解,
从而确定参数的值或取值范围.
高 考 回 眸 【p18】
考题1[2018·全国卷Ⅰ]设x,y满足约束条件则z=3x+2y的最大值为__________.
【解析】6
作出可行域为如图所示的△ABC所表示的阴影区域,作出直线3x+2y=0,并平移该直线,当直线过点A(2,0)时,目标函数z=3x+2y取得最大值,且zmax=3×2+2×0=6.
【命题立意】 本题考查简单的线性规划,考查学生的转化与化归能力、运算求解能力,考查的数学核心素养是逻辑推理、数学运算.
考题2[2015·全国卷Ⅰ]设x、y满足约束条件则的最大值为__________.
【解析】3
的几何意义为点(x,y)与坐标原点连线的斜率.
画出可行域,如图中阴影部分所示.
由得C(1,3),
由题易知可行域上的C点与坐标原点连线的斜率最大,且最大值为3.
【命题立意】本题考查简单的线性规划,考查学生的转化与化归能力、运算求解能力,考查的数学核心素养是逻辑推理、数学运算.
考题3[2016·全国卷Ⅰ]某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元.
【解析】216 000
设生产产品A、产品B分别为x件、y件,利润之和为z元,则
即
目标函数为z=2 100x+900y.
作出二元一次不等式组表示的平面区域为图中阴影部分内(包括边界)的整点,即可行域.
由图可知当直线z=2 100x+900y经过点M时,z取得最大值.
解方程组得M的坐标为(60,100),
所以当x=60,y=100时,zmax=2 100×60+900×100=216 000.
【命题立意】本题考查简单的线性规划,考查学生的分析问题、解决问题的能力,转化与化归能力、运算求解能力,考查的数学核心素养是逻辑推理、数学运算.
考点限时训练 【p115】
A组 基础演练
1.设x,y满足约束条件则z=x+y的最大值为( )
A.0 B.1 C.2 D.3
【解析】选D.
作出约束条件对应的可行域,如图中阴影部分所示,当直线z=x+y经过可行域中的点A(3,0)时,目标函数取得最大值,故zmax=3.
2.设变量x,y满足约束条件则lg(y+1)-lg x的取值范围是( )
A.[0,1-2lg 2] B.
C. D.
【解析】选A.
如图,作出不等式组
确定的可行域:
因为lg(y+1)-lg x=lg,设t=,
显然,t的几何意义是可行域内的点P(x,y)与定点E(0,-1)连线的斜率.
由图可知,P点与B点重合时,t取得最小值,P点与C点重合时,t取得最大值.
由解得即B(3,2);
由解得即C(2,4).
故t的最小值为kBE==1,
t的最大值为kCE==,所以t∈.
又函数y=lg x为(0,+∞)上的增函数,
所以lg t∈,
即lg(y+1)-lg x的取值范围为.
而lg=1-2lg 2,
所以lg(y+1)-lg x的取值范围为[0,1-2lg 2].选A.
3.已知函数f(x)= 设a∈R,若关于x的不等式f(x)≥在R上恒成立,则a的取值范围是( )
A. B.
C.[-2,2] D.
【解析】 选A.
由已知可得f(x)>0.不等式f(x)≥可转化为-f(x)≤+a≤f(x).当x≤1时,有-x2+x-3≤+a≤x2-x+3,即-x2+-3≤a≤x2-x+3,又∵-x2+x-3=--≤-,x2-x+3=+≥,∴-≤a≤.当x>1时,-x-≤+a≤x+,即-x-≤a≤x+,又∵-x-≤-2,x+≥2,∴-2≤a≤2.故-≤a≤2.
4.若不等式logax>sin 2x(a>0,a≠1)对任意x∈都成立,则a的取值范围为( )
A. B.
C. D.(0,1)
【解析】选B.
记y1=logax,y2=sin 2x,原不等式相当于y1>y2.作出两个函数的图象,如图所示,
知当y1=logax过点A时,a=,所以当≤a<1时,对任意x∈都有y1>y2.
5.设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为( )
A.(1,1+) B.(1+,+∞)
C.(1,3) D.(3,+∞)
【解析】选A.
画出可行域,可知z=x+my在点处取最大值,
由+<2解得1m(x2-1)对所有-2≤m≤2都成立,则x的取值范围为________.
【解析】
原不等式化为:m(x2-1)-(2x-1)<0,
令f(m)=m(x2-1)-(2x-1).
当-2≤m≤2时,f(m)<0恒成立,只需满足即
解得
查看更多