2021版高考数学一轮复习第四章三角函数解三角形第六节正弦定理和余弦定理课件文北师大版

2021版高考数学一轮复习第四章三角函数解三角形第六节正弦定理和余弦定理课件文北师大版

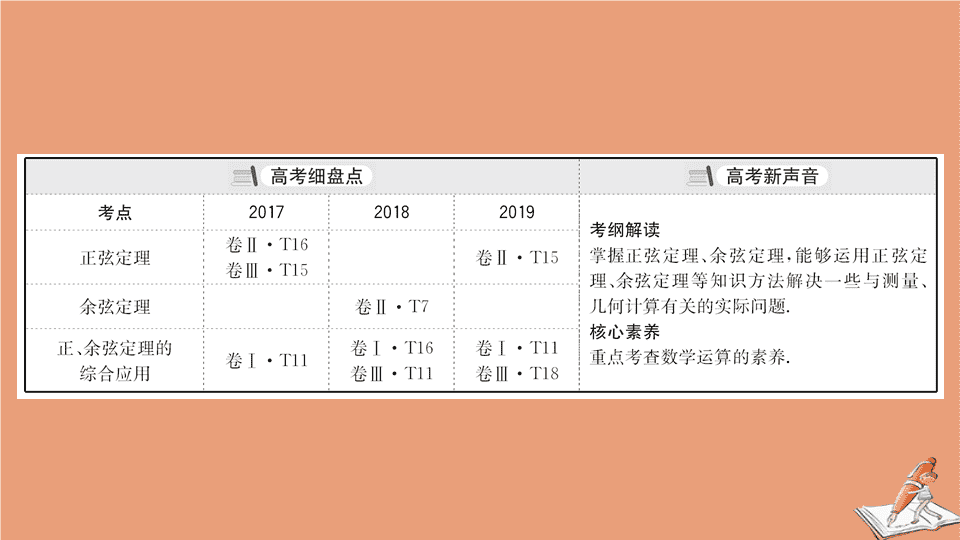
第六节　正弦定理和 余弦定理 内容索引 必备知识 · 自主学习 核心考点 · 精准研析 核心素养 · 微专题 核心素养测评 【 教材 · 知识梳理 】 1. 正弦定理 (1) 定理 : 在△ ABC 中 , 其中 R 为△ ABC 的外接圆半径 . (2) 运用方法 适用情形 : 两角 A,B 及其对边 a,b( 知三求一 ). 列方程 : . (3) 变形 :a=2Rsin A,sin A= ,a∶b∶c=sin A∶sin B∶sin C 等 . 2. 余弦定理 (1) 定理 : 在△ ABC 中 ,a 2 =b 2 +c 2 -2bccos A, b 2 =c 2 +a 2 -2accos B, c 2 = ______________.  (2) 运用方法 适用情形 : 三边 a,b,c, 任一内角 A( 知三求一 ). 列方程 :a 2 =b 2 +c 2 -2bccos A 或 cos A= ___________ . a 2 +b 2 -2abcos C (3) 变形 :cos A= , b 2 +c 2 -a 2 =2bccos A 等等 . 3. 三角形面积公式 (1) 正弦定理推论 : S △ABC = absin C= bcsin A= .  (2) 其他常用公式方法 S= 底 × 高 ;S= absin C;S= ×C×r,(C 为周长 ,r 为内切圆半径 ) 等等 . 【 知识点辨析 】 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 在△ ABC 中 , 已知 a,b 和角 B, 能用正弦定理求角 A; 已知 a,b 和角 C, 能用余弦定理求边 c. ( 　　 ) (2) 在三角形中 , 已知两角和一边或已知两边和一角都能解三角形 . ( 　　 ) (3) 在△ ABC 中 ,sin A>sin B 的充分不必要条件是 A>B.( 　　 ) 提示 : 根据正弦定理和余弦定理知 (3) 是错误的 ,(1)(2) 是正确的 . 【 易错点索引 】 序号 易错警示 典题索引 1 在三角形中 , 一个正弦值 ( 正数 ) 对应两个角 , 一个余弦值对应一个角 考点一、 T3 2 忽视三角形内角范围 , 即 0°0, 于 是有 cos B<0,B 为钝角 ,△ABC 是钝角三角形 . 3.( 必修 5P56A 组 T3 改编 ) 已知在△ ABC 中 ,A= ,B= ,a=1, 则 b 等于 ( 　　 ) 【 解析 】 选 D. 由正弦定理 4.( 必修 5P56A 组 T6 改编 ) 在△ ABC 中 ,A=60°,AC=4,BC= , 则△ ABC 的面积等于 　　　　 .  【 解析 】 设△ ABC 中 , 角 A,B,C 对应的边分别为 a,b,c. 由题意及余弦定理得 解得 c=2. 所以 答案 : 核心素养　数学运算 —— 正余弦定理结合三角变换　  【 素养诠释 】 数学运算是在明晰运算对象的基础上 , 依据运算法则解决数学问题的过程 . 主要包括 : 理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等 . 【 典例 】 (2019· 西安模拟 ) 在△ ABC 中 , 内角 A,B,C 所对的边分别为 a,b,c. 已知 asin A=4bsin B,ac= (a 2 -b 2 -c 2 ). 世纪金榜导学号 (1) 求 cos A 的值 . (2) 求 sin (2B-A) 的值 . 【 素养立意 】 　 与三角恒等变换相结合 , 考查正弦定理、余弦定理 . 【 解析 】 (1) 由 asin A=4bsin B 及 得 a=2b. 由 ac= (a 2 -b 2 -c 2 ), 及余弦定理得 (2) 由 (1) 及 A∈(0, π ), 可得 sin A= , 代入 asin A=4bsin B, 得 由 (1) 知 ,A 为钝角 , 所以 于是 sin 2B=2sin Bcos B= ,cos 2B=1-2sin 2 B= , 故 sin (2B-A)=sin 2Bcos A-cos 2Bsin A