江苏省无锡辅仁高级中学2019-2020学年高二下学期期中考试数学试题

江苏省无锡辅仁高级中学2019-2020学年高二下学期期中考试数学试题

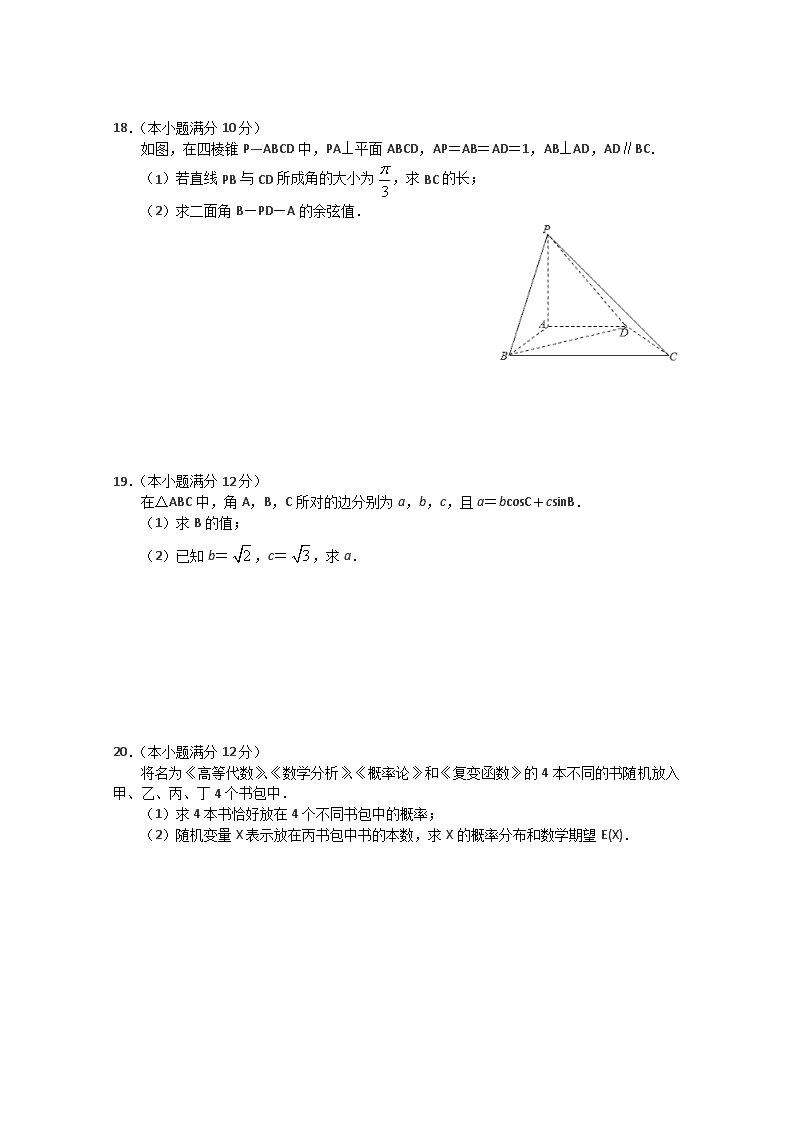
江苏省无锡辅仁高级中学2019—2020学年高二下学期期中考试 数学试题 ‎2020．5‎ 一、选择题（本大题共12小题，每小题5分，共计60分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎1．已知集合A＝{﹣1，0，1}，B＝，则AB＝‎ ‎ A．{﹣1，0，1} B．{1} C．{﹣1，1} D．{0，1}‎ ‎2．已知x，yR，则“x＝y”是“”的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎3．已知双曲线(a＞0，b＞0)的离心率为，则双曲线的渐近线方程为 ‎ A． B． C． D．‎ ‎4．在△ABC中，a，b，c分别为角A，B，C所对边，若a＝2bcosC，则此三角形一定是 ‎ A．等腰直角三角形 B．直角三角形 C．等腰三角形 D．等腰或直角三角形 ‎5．已知，，，则a，b，c的大小关系为 ‎ A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b ‎6．已知，则等于 ‎ A．29 B．49 C．39 D．1‎ ‎7．若是方程的解，则属于区间 ‎ A．(，1) B．(，) C．(，) D．(0，)‎ ‎8．已知函数的图象向左平移(0＜＜)个单位后，其图象关于y轴对称，则的值为 ‎ A． B． C． D．‎ ‎9．已知双曲线的中心在原点，离心率为，若它的一条准线与抛物线的准线重合，则该双曲线与抛物线的交点到原点的距离是 ‎ A． B． C． D．21‎ ‎10．已知函数在区间[0，1]上不单调，则实数m的取值范围为 ‎ A．[1，e] B．(1，e) C．[1，e2] D．(1，e2)‎ ‎11．从5位男教师和4位女教师中选出3位教师，派到3个班担任班主任（每班1位班主任），要求这3位班主任中男、女教师都要有，则不同的选派方案共有 ‎ A．210种 B．420种 C．630种 D．840种 ‎12．在△ABC中，AB＝2，D，E分别是边AB，AC的中点，CD与BE交于点O，若OC＝OB，则△ABC面积的最大值为 ‎ A． B． C． D．‎ 二、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）‎ ‎13．已知是奇函数，且当x＞0时，，则＝ ．‎ ‎14．若对于任意的实数x，有，则的值为 ．‎ ‎15．已知正实数x，y满足，则的最大值是 ．‎ ‎16．规定：若函数在定义域[m，n](1＜m＜n)上的值域是[m3，n3]，则称该函数为“绅士风度”函数．已知函数(a＞0且a≠1)为“绅士风度”函数，则a的取值范围是 ．‎ 三、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）‎ 如图，设点A是单位圆O和x轴正半轴的交点，O是坐标原点，P，Q是单位圆上的两点，∠AOP＝，∠AOQ＝，[0，)．‎ ‎（1）若Q(，)，求的值；‎ ‎（2）设函数，求的值域．‎ ‎18．（本小题满分10分）‎ 如图，在四棱锥P—ABCD中，PA⊥平面ABCD，AP＝AB＝AD＝1，AB⊥AD，AD∥BC．‎ ‎（1）若直线PB与CD所成角的大小为，求BC的长；‎ ‎（2）求二面角B—PD—A的余弦值．‎ ‎19．（本小题满分12分）‎ 在△ABC中，角A，B，C所对的边分别为a，b，c，且a＝bcosC＋csinB．‎ ‎（1）求B的值；‎ ‎（2）已知b＝，c＝，求a．‎ ‎20．（本小题满分12分）‎ 将名为《高等代数》、《数学分析》、《概率论》和《复变函数》的4本不同的书随机放入甲、乙、丙、丁4个书包中．‎ ‎（1）求4本书恰好放在4个不同书包中的概率；‎ ‎（2）随机变量X表示放在丙书包中书的本数，求X的概率分布和数学期望E(X)．‎ ‎21．（本小题满分12分）‎ 已知椭圆C：(a＞b＞0)，A(a，0)，B(0，b)，O(0，0)，若△OAB的面积为1，且过右焦点F垂直于x轴的直线被椭圆C截得的线段长为1．‎ ‎（1）求椭圆C的方程；‎ ‎（2）设P是椭圆C上一点，直线PA与y轴交于点M，直线PB与x轴交于点N，试问AN·BM是否为定值，若是，求出该定值，若不是，请说明理由．‎ ‎22．（本小题满分14分）‎ 已知函数．‎ ‎（1）若m＝1，n＝0，求函数的单调区间；‎ ‎（2）若m＝1，n＝1，求函数在区间[2a，4a]上的最小值；‎ ‎（3）某高二学习研究小组通过研究发现：总存在正实数a，b(a＜b)，使等式成立．试问：他们的研究成果是否确？若正确，请写出a，b的取值范围；若不正确，请说明理由．‎ 参考答案 ‎1．B 2．A 3．C 4．C 5．D 6．B 7．C 8．A ‎9．B 10．D 11．B 12．C ‎13．﹣8 14．37 15． 16．(1，)‎ ‎17．‎ ‎ ‎ ‎18．‎ ‎ ‎ ‎19．解：（1）∵a＝bcosC＋csinB，‎ ‎∴sinA＝sinBcosC＋sinCsinB，‎ 又∵sinA＝sin[π﹣(B＋C)]＝sin(B＋C)＝sinBcosC＋cosBsinC，‎ ‎∴sinBcosC＋sinCsinB＝sinBcosC＋cosBsinC，即sinCsinB＝cosBsinC，‎ ‎∵cosBsinC≠0，等是两边同时除以cosBsinC得 ‎∴tanB＝1，0＜B＜π，∴B＝，‎ ‎（2）由余弦定理，‎ 得，即，‎ 解得．‎ ‎20．‎ ‎21．‎ ‎ ‎ ‎ ‎ ‎22．‎