2021版高考数学一轮复习第三章导数及其应用3-4-3导数的存在性问题练习苏教版

2021版高考数学一轮复习第三章导数及其应用3-4-3导数的存在性问题练习苏教版

‎3.4.3 导数的存在性问题 考点一　关于函数零点或方程的根的存在性问题 ‎ ‎【典例】1.(2020·泰安模拟)若函数f(x)=ax3-x2+1存在唯一的零点x0,且x0>0,则实数a的取值范围是(　　)‎ A. B.(-,0)‎ C.(0,) D.‎ ‎2.(2020·扬州模拟)已知函数f(x)= 若方程[f(x)]2=a恰有两个不同的实数根x1,x2,则x1+x2的最大值是________. 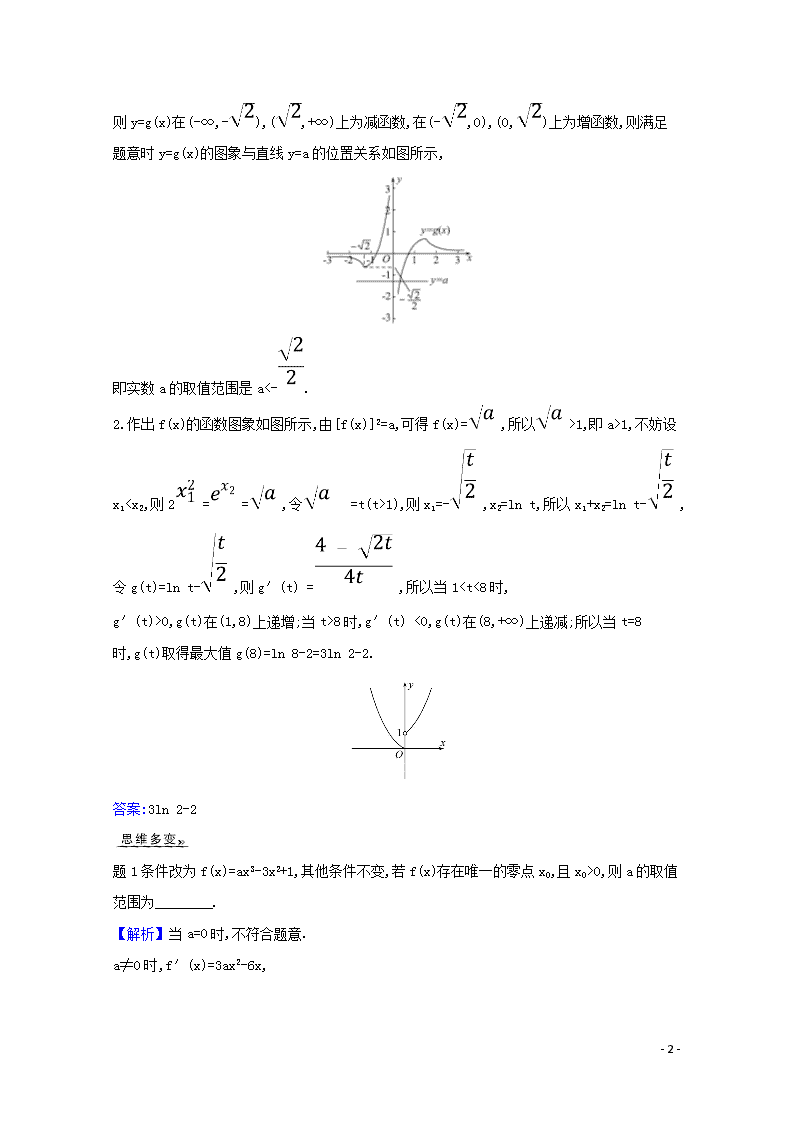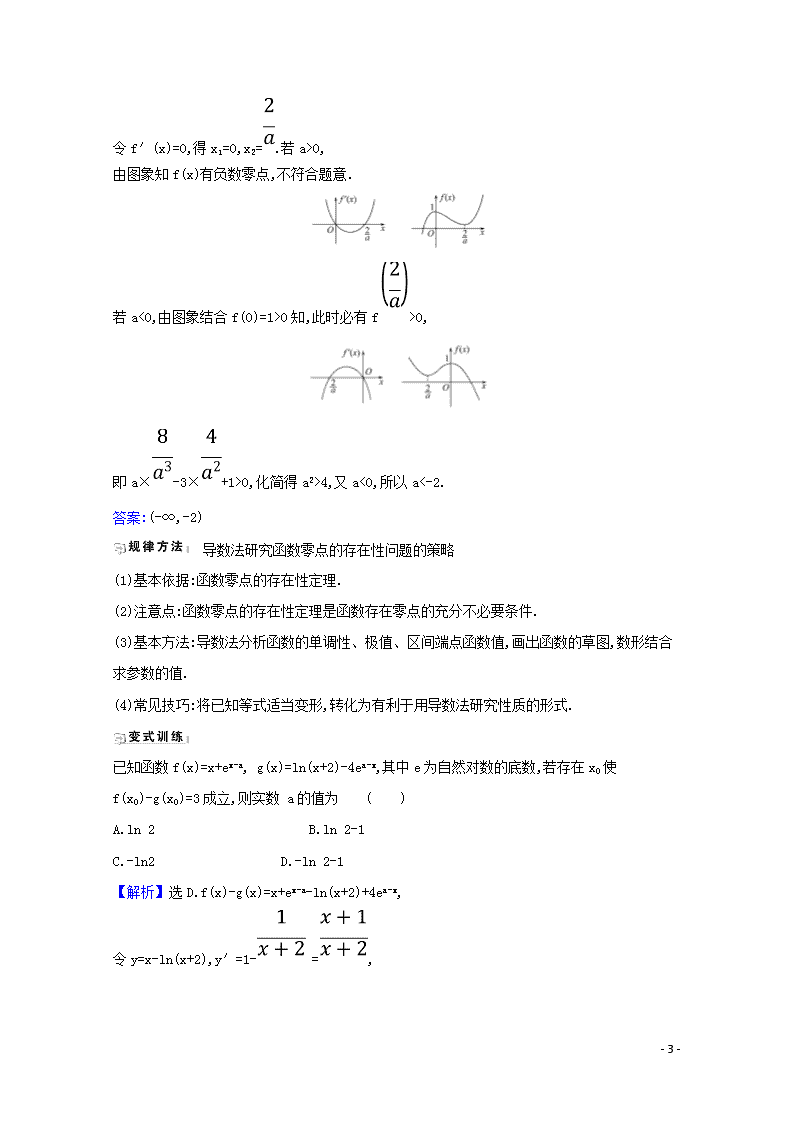‎ ‎【解题导思】‎ 序号 联想解题 ‎1‎ 由存在唯一的零点x0,且x0>0,想到分离变量a构建新函数 ‎2‎ 由[f(x)]2=a恰有两个不同的实数根,想到f(x)= ,数形结合求x1,x2,构建函数.‎ ‎【解析】1.选A.由函数f(x)=ax3-x2+1存在唯一的零点x0,且x0>0等价于a=有唯一正根,‎ 即函数y=g(x)=的图象与直线y=a在y轴右侧有1个交点,‎ 又y=g(x)为奇函数且g′(x)=,‎ - 10 -‎ 则y=g(x)在(-∞,-),(,+∞)上为减函数,在(-,0),(0,)上为增函数,则满足题意时y=g(x)的图象与直线y=a的位置关系如图所示,‎ 即实数a的取值范围是a<-.‎ ‎2.作出f(x)的函数图象如图所示,由[f(x)]2=a,可得f(x)= ,所以 >1,即a>1,不妨设x11),则x1=- ,x2=ln t,所以x1+x2=ln t- ,令g(t)=ln t- ,则g′(t) = ,所以当10,g(t)在(1,8)上递增;当t>8时,g′(t) <0,g(t)在(8,+∞)上递减;所以当t=8时,g(t)取得最大值g(8)=ln 8-2=3ln 2-2.‎ 答案:3ln 2-2‎ 题1条件改为f(x)=ax3-3x2+1,其他条件不变,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围为________. ‎ ‎【解析】当a=0时,不符合题意.‎ a≠0时,f′(x)=3ax2-6x,‎ - 10 -‎ 令f′(x)=0,得x1=0,x2=.若a>0,‎ 由图象知f(x)有负数零点,不符合题意.‎ 若a<0,由图象结合f(0)=1>0知,此时必有f>0,‎ 即a×-3×+1>0,化简得a2>4,又a<0,所以a<-2.‎ 答案:(-∞,-2)‎ ‎　导数法研究函数零点的存在性问题的策略 ‎(1)基本依据:函数零点的存在性定理.‎ ‎(2)注意点:函数零点的存在性定理是函数存在零点的充分不必要条件.‎ ‎(3)基本方法:导数法分析函数的单调性、极值、区间端点函数值,画出函数的草图,数形结合求参数的值.‎ ‎(4)常见技巧:将已知等式适当变形,转化为有利于用导数法研究性质的形式.‎ ‎ ‎ 已知函数f(x)=x+ex-a, g(x)=ln(x+2)-4ea-x,其中e为自然对数的底数,若存在x0使f(x0)-g(x0)=3成立,则实数 a的值为 (　　)‎ A.ln 2　 B.ln 2-1‎ C.-ln2 D.-ln 2-1 ‎ ‎【解析】选D.f(x)-g(x)=x+ex-a-ln(x+2)+4ea-x,‎ 令y=x-ln(x+2),y′=1- =,‎ - 10 -‎ 故y=x-ln(x+2)在(-2,-1)上是减函数,(-1,+∞)上是增函数,故当x=-1时,y有最小值-1-0=-1,而ex-a+4ea-x≥4(当且仅当ex-a=4ea-x,即x=a+ln 2时,等号成立);故f(x)-g(x)≥3(当且仅当等号同时成立时,等号成立);故a+ln 2=-1,即a=-1-ln 2.‎ 考点二　关于函数极值、最值的存在性问题 ‎ ‎【典例】(2019·大连模拟)已知x=1是函数f(x)=ax2+-xln x的极值点. ‎ ‎(1)求实数a的值.‎ ‎(2)求证:函数f(x)存在唯一的极小值点x0,且00 ,f(x) 为增函数;‎ 当12时,g′(x)>0,g(x)为增函数,且g(4)=-2ln 2>0 ,g(2)<0,‎ 所以存在x0∈(2,4),g(x0)=0.当2x>x0 时,g(x)>0 ,f(x) 为增函数,所以函数f(x)存在唯一的极小值点x0.‎ 又g=-ln ,已知16e5<74 ,可得e5<⇒5<4ln ,所以g<0,所以a-5,求实数a的取值范围.‎ ‎【解析】(1)f(x)的定义域为(0,+∞),‎ 由已知得f′(x)=-a,‎ 当a<0时,f′(x)>0,‎ 所以,f(x)在(0,+∞)内单调递增,无减区间;‎ - 10 -‎ 当a>0时,令f′(x)=0,得x=,‎ 所以当x∈时f′(x)>0,f(x)单调递增;‎ 当x∈时f′(x)<0,f(x)单调递减.‎ ‎(2)由(1)知,当a<0时,f(x)在(0,+∞)内单调递增,无最大值,‎ 当a>0时,函数f(x)在x=取得最大值,‎ 即f(x)max=f=ln -4=-ln a-4,‎ 因此有-ln a-4>a-5,得ln a+a-1<0,‎ 设g(a)=ln a+a-1,则g′(a)=+1>0,所以g(a)在(0,+∞)内单调递增,‎ 又g(1)=0,所以g(a)0;‎ 所以当x=1时,f(x)取最小值,为,‎ 因此∃x∈[1,2],使得≥-x2-2ax+4成立,所以a≥,因为y=-+在[1,2]上单调递减,所以y=-+的最小值为-+=-,因此a≥-.‎ ‎2.已知函数f(x)=ax-ex(a∈R),g(x)=. ‎ ‎(1)求函数f(x)的单调区间.‎ ‎(2)∃x0∈(0,+∞),使不等式f(x)≤g(x)-ex成立,求a的取值范围.‎ ‎【解题导思】‎ 序号 题目拆解 ‎(1)函数f(x)的单调区间 求f′(x),依据f′(x)=0解的情况,分类讨论 ‎(2)∃x0∈(0,+∞),使不等式f(x)≤g(x)-ex成立 对不等式适当变形,转化为求函数最值问题 ‎【解析】(1)因为f′(x)=a-ex,x∈R.‎ 当a≤0时,f′(x)<0,f(x)在R上单调递减;‎ 当a>0时,令f′(x)=0得x=ln a.‎ - 10 -‎ 由f′(x)>0得f(x)的单调递增区间为(-∞,ln a);‎ 由f′(x)<0得f(x)的单调递减区间为(ln a,+∞).‎ 综上,当a≤0时,f(x)的单调减区间为R;当a>0时,f(x)的单调增区间为(-∞,‎ ln a);‎ 单调减区间为(ln a,+∞).‎ ‎(2)因为∃x0∈(0,+∞),使不等式f(x)≤g(x)-ex,‎ 所以ax≤,即a≤.‎ 设h(x)=,则问题转化为a≤,‎ 由h′(x)=,令h′(x)=0,则x=.‎ 当x在区间(0,+∞)内变化时,h′(x),h(x)的变化情况如下表:‎ x ‎(0,)‎ ‎(,+∞)‎ h′(x)‎ ‎+‎ ‎0‎ ‎-‎ h(x)‎ ‎↗‎ 极大值 ‎↘‎ 由上表可知,当x=时,函数h(x)有极大值,即最大值为.所以a≤.‎ ‎1.不等式存在性问题的求解策略 ‎“恒成立”与“存在性”问题的求解是“互补”关系,即f(x)≥g(a)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,应求f(x)的最大值.在具体问题中究竟是求最大值还是最小值,可以先联想“恒成立”是求最大值还是最小值,这样也就可以解决相应的“存在性”问题是求最大值还是最小值.特别需要关注等号是否成立,以免细节出错.‎ ‎2.两个常用结论 ‎(1)∃x∈I,使得f(x)>g(x)成立⇔[f(x)-g(x)]max>0(x∈I).‎ - 10 -‎ ‎(2)对∀x1∈D1,∃x2∈D2使得f(x1)≥g(x2)⇔f(x)min≥g(x)min,f(x)的定义域为D1,g(x)的定义域为D2.‎ ‎　已知f(x)=ln x-x+a+1.‎ ‎(1)若存在x∈(0,+∞),使得f(x)≥0成立,求实数a的取值范围.‎ ‎(2)求证:当x>1时,在(1)的条件下,x2+ax-a>xln x+成立.‎ ‎【解析】f(x)=ln x-x+a+1(x>0).‎ ‎(1)原题即为存在x∈(0,+∞)使得ln x-x+a+1≥0,‎ 所以a≥-ln x+x-1,‎ 令g(x)=-ln x+x-1,‎ 则g′(x)=-+1=.‎ 令g′(x)=0,解得x=1.‎ 因为当01时,g′(x)>0,所以g(x)为增函数,‎ 所以g(x)min=g(1)=0.所以a≥g(1)=0.‎ 所以a的取值范围为[0,+∞).‎ ‎(2)原不等式可化为x2+ax-xln x-a->0(x>1,a≥0).‎ 令G(x)=x2+ax-xln x-a-,‎ 则G(1)=0.‎ 由(1)可知x>1时,x-ln x-1>0,则G′(x)=x+a-ln x-1‎ ‎≥x-ln x-1>0,‎ 所以G(x)在(1,+∞)上递增,‎ 所以当x>1时,G(x)>G(1)=0.‎ 所以当x>1时,x2+ax-xln x-a->0成立,‎ - 10 -‎ 即当x>1时,x2+ax-a>xln x+成立.‎ - 10 -‎